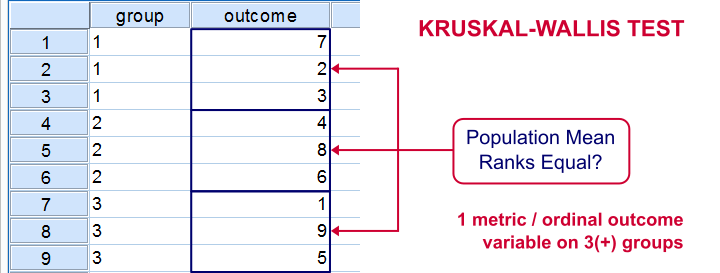
The Kruskal-Wallis test is an alternative for a one-way ANOVA if the assumptions of the latter are violated. We'll show in a minute why that's the case with creatine.sav, the data we'll use in this tutorial. But let's first take a quick look at what's in the data anyway.
Quick Data Description

Our data contain the result of a small experiment regarding creatine, a supplement that's popular among body builders. These were divided into 3 groups: some didn't take any creatine, others took it in the morning and still others took it in the evening. After doing so for a month, their weight gains were measured. The basic research question is
does the average weight gain depend on
the creatine condition to which people were assigned?
That is, we'll test if three means -each calculated on a different group of people- are equal. The most likely test for this scenario is a one-way ANOVA but using it requires some assumptions. Some basic checks will tell us that these assumptions aren't satisfied by our data at hand.
Data Check 1 - Histogram
A very efficient data check is to run histograms on all metric variables. The fastest way for doing so is by running the syntax below.
frequencies gain
/formats notable
/histogram.
Histogram Result
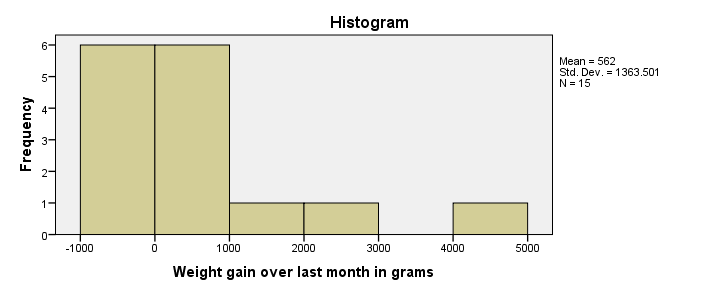
First, our histogram looks plausible with all weight gains between -1 and +5 kilos, which are reasonable outcomes over one month. However, our outcome variable is not normally distributed as required for ANOVA. This isn't an issue for larger sample sizes of, say, at least 30 people in each group. The reason for this is the central limit theorem. It basically states that for reasonable sample sizes the sampling distribution for means and sums are always normally distributed regardless of a variable’s original distribution. However, for our tiny sample at hand, this does pose a real problem.
Data Check 2 - Descriptives per Group
Right, now after making sure the results for weight gain look credible, let's see if our 3 groups actually have different means. The fastest way to do so is a simple MEANS command as shown below.
means gain by group.
SPSS MEANS Output
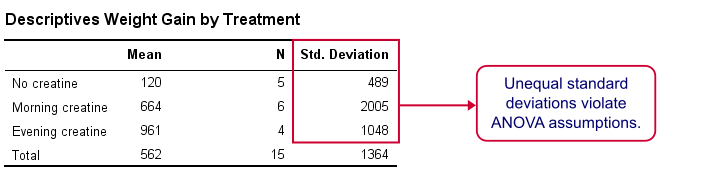
First, note that our evening creatine group (4 participants) gained an average of 961 grams as opposed to 120 grams for “no creatine”. This suggests that creatine does make a real difference.
But don't overlook the standard deviations for our groups: they are very different but ANOVA requires them to be equal.The assumption of equal population standard deviations for all groups is known as homoscedasticity. This is a second violation of the ANOVA assumptions.
Kruskal-Wallis Test
So what should we do now? We'd like to use an ANOVA but our data seriously violates its assumptions. Well, a test that was designed for precisely this situation is the Kruskal-Wallis test which doesn't require these assumptions. It basically replaces the weight gain scores with their rank numbers and tests whether these are equal over groups. We'll run it by following the screenshots below.
Running a Kruskal-Wallis Test in SPSS
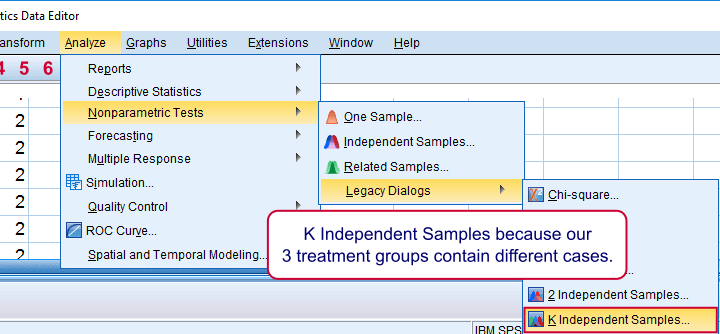
We use if we compare 3 or more groups of cases. They are “independent” because our groups don't overlap (each case belongs to only one creatine condition).
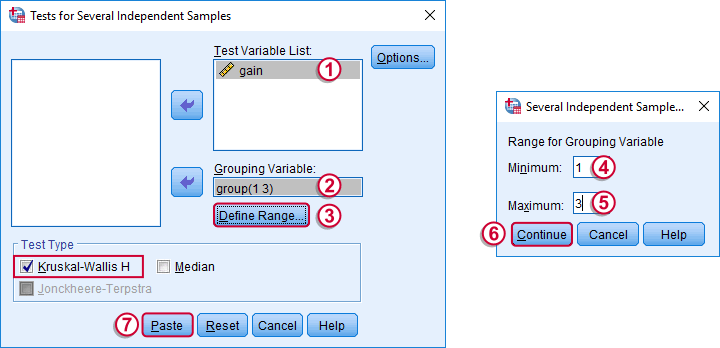
Depending on your license, your SPSS version may or may have the option shown below. It's fine to skip this step otherwise.
SPSS Kruskal-Wallis Test Syntax
Following the previous screenshots results in the syntax below. We'll run it and explain the output.
NPAR TESTS
/K-W=gain BY group(1 3)
/MISSING ANALYSIS.
SPSS Kruskal-Wallis Test Output
We'll skip the “RANKS” table and head over to the “Test Statistics” shown below.
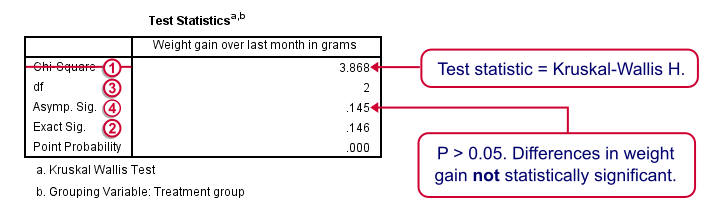
 Our test statistic -incorrectly labeled as “Chi-Square” by SPSS- is known as Kruskal-Wallis H. A larger value indicates larger differences between the groups we're comparing. For our data it's roughly 3.87. We need to know its sampling distribution for evaluating whether this is unusually large.
Our test statistic -incorrectly labeled as “Chi-Square” by SPSS- is known as Kruskal-Wallis H. A larger value indicates larger differences between the groups we're comparing. For our data it's roughly 3.87. We need to know its sampling distribution for evaluating whether this is unusually large.
 Exact Sig. uses the exact (but very complex) sampling distribution of H. However, it turns out that if each group contains 4 or more cases, this exact sampling distribution is almost identical to the (much simpler) chi-square distribution.
Exact Sig. uses the exact (but very complex) sampling distribution of H. However, it turns out that if each group contains 4 or more cases, this exact sampling distribution is almost identical to the (much simpler) chi-square distribution.
 We therefore usually approximate the p-value with a chi-square distribution. If we compare k groups, we have k - 1 degrees of freedom, denoted by df in our output.
We therefore usually approximate the p-value with a chi-square distribution. If we compare k groups, we have k - 1 degrees of freedom, denoted by df in our output.
 Asymp. Sig. is the p-value based on our chi-square approximation. The value of 0.145 basically means there's a 14.5% chance of finding our sample results if creatine doesn't have any effect in the population at large. So if creatine does nothing whatsoever, we have a fair (14.5%) chance of finding such minor weight gain differences just because of random sampling. If p > 0.05, we usually conclude that our differences are not statistically significant.
Asymp. Sig. is the p-value based on our chi-square approximation. The value of 0.145 basically means there's a 14.5% chance of finding our sample results if creatine doesn't have any effect in the population at large. So if creatine does nothing whatsoever, we have a fair (14.5%) chance of finding such minor weight gain differences just because of random sampling. If p > 0.05, we usually conclude that our differences are not statistically significant.
Note that our exact p-value is 0.146 whereas the approximate p-value is 0.145. This supports the claim that H is almost perfectly chi-square distributed.
Kruskal-Wallis Test - Reporting
The official way for reporting our test results includes our chi-square value, df and p as in
“this study did not demonstrate any effect from creatine,
H(2) = 3.87, p = 0.15.”
So that's it for now. I hope you found this tutorial helpful. Please let me know by leaving a comment below. Thanks!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 71 COMMENTS:
By Ruben Geert van den Berg on August 24th, 2017
Hi John!
First off, your dependent variables seem to be metric ("scale"). In this case, you can compute means by factor and perhaps visualize these with bar charts (with/without standard error bars). I think that'll be more interesting than just more statistical significance tests.
I'm not sure if you should go with K-W instead of ANOVA in the first place. There's the Welch statistic for unequal variances and Games-Howell post hoc for this case. Violations of normality don't really seem too serious. And what about the sample sizes of the groups you're comparing?
1. Andy Field discusses these approaches but I don't have his book here right now.
2. I'd say: exclude test-by-test (pairwise deletion). This makes use of more data points but different tests may be based on different subsamples. Why should you exclude cases that have a missing on B while testing A? Or choose the option that gives the best results and don't say much about your choice in your report ;-) OH NO! WHAT DID I JUST SAY??!?
3. What exactly did you read? I think Dunn-Bonferroni assumes equal variances/normality but I'm not 100% sure on that (I believe Field says something about it).
Kind regards,
Ruben
By John on August 24th, 2017
Thanks Ruben,
My dependent variables (biomarkers) are scale and my independent variables (sites) are nominal. I have figures that have the means of the biomarkers by site with standard error bars, but I want to indicate on these figures any significant differences determined by ANOVA or K-W.
In all of the other literature that I've seen, an ANOVA is used to compare differences in biomarker levels by site, unless there are violations of equal variances/normality that justify the use of K-W. I have not seen the Welch statistic and G-H post hoc used.
For one biomarker, the sample sizes are 8, 9, and 10 for the 3 sites. For another biomarker, the sample sizes are 10, 14, and 30.
2. I'm not sure what you mean by "Why should you exclude cases that have a missing on B while testing A?" in terms of excluding cases test-by-test or listwise. The literature doesn't seem to specify the post hoc method used for K-W, they just state that it was used if violations were observed in the data. Maybe this ambiguity allows me to make the decision myself.
3. The IBM Support link below for SPSS says that the Dunn-Bonferroni post hoc method was added for pairwise comparisons in which the K-W was statistically significant. I don't believe that D-B assumes equal variances/normality since it is a post hoc for K-W. In this case I just don't know whether to exclude cases test-by-test or listwise.
http://www-01.ibm.com/support/docview.wss?uid=swg21479073
By Ruben Geert van den Berg on August 24th, 2017
Hi John!
Welch and G-H are recommended (for ANOVA) by Andy Field who seems to have studied the issue pretty thoroughly. However, given the small -and sometimes sharply unequal- sample sizes, I think KW is playing it safely.
The CSR (version 24) doesn't mention anything about any Dunn test whatsoever. Honestly, I may have mixed it up with Dunnett perhaps in my previous reply. I never heard of any Dunn test anyway. Sorry!
Exclude cases test by test. Listwise will only use cases that have zero missings on all variables for all tests. "Test by test" means SPSS will use all cases it can for each test separately. If you'd use a separate SPSS command for each test, you'd implicitly use "test by test".
Hope that helps!
Ruben
By Ha My on November 9th, 2017
Hi,
I want to ask if the number of variable are not the same Can I still use Kruskal-Wallis Test. For example, pea plant is growth in 4 different type of soil. 6 for each pot. Then the total will be 24 peas, but in 1 pot only 5 germinate while the rest all germinate. Then the total value will be 23, can I assign the death pea as 0 or not
By Ruben Geert van den Berg on November 9th, 2017
Hi Ha My!
You can use the KW-test to compare groups of unequal sizes. So samples of 3, 5, 5 and 10 observations don't pose any problem.
If a pea does not germinate at all, you may want to exclude it from your data altogether. Or give it a zero value but that really depends on what you're measuring and if your zero value truly means "nothing" -which is not always the case.