The Kruskal-Wallis test is an alternative for a one-way ANOVA if the assumptions of the latter are violated. We'll show in a minute why that's the case with creatine.sav, the data we'll use in this tutorial. But let's first take a quick look at what's in the data anyway.
Quick Data Description

Our data contain the result of a small experiment regarding creatine, a supplement that's popular among body builders. These were divided into 3 groups: some didn't take any creatine, others took it in the morning and still others took it in the evening. After doing so for a month, their weight gains were measured. The basic research question is
does the average weight gain depend on
the creatine condition to which people were assigned?
That is, we'll test if three means -each calculated on a different group of people- are equal. The most likely test for this scenario is a one-way ANOVA but using it requires some assumptions. Some basic checks will tell us that these assumptions aren't satisfied by our data at hand.
Data Check 1 - Histogram
A very efficient data check is to run histograms on all metric variables. The fastest way for doing so is by running the syntax below.
frequencies gain
/formats notable
/histogram.
Histogram Result
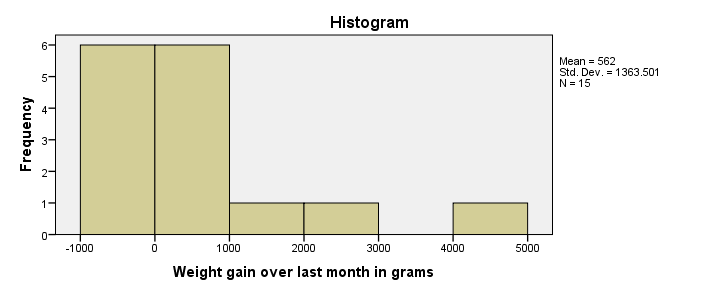
First, our histogram looks plausible with all weight gains between -1 and +5 kilos, which are reasonable outcomes over one month. However, our outcome variable is not normally distributed as required for ANOVA. This isn't an issue for larger sample sizes of, say, at least 30 people in each group. The reason for this is the central limit theorem. It basically states that for reasonable sample sizes the sampling distribution for means and sums are always normally distributed regardless of a variable’s original distribution. However, for our tiny sample at hand, this does pose a real problem.
Data Check 2 - Descriptives per Group
Right, now after making sure the results for weight gain look credible, let's see if our 3 groups actually have different means. The fastest way to do so is a simple MEANS command as shown below.
means gain by group.
SPSS MEANS Output
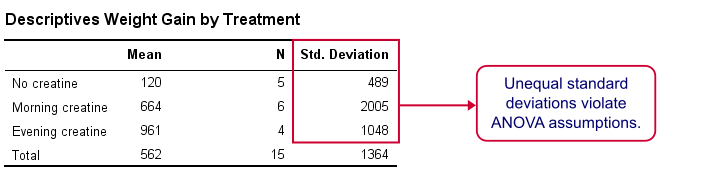
First, note that our evening creatine group (4 participants) gained an average of 961 grams as opposed to 120 grams for “no creatine”. This suggests that creatine does make a real difference.
But don't overlook the standard deviations for our groups: they are very different but ANOVA requires them to be equal.The assumption of equal population standard deviations for all groups is known as homoscedasticity. This is a second violation of the ANOVA assumptions.
Kruskal-Wallis Test
So what should we do now? We'd like to use an ANOVA but our data seriously violates its assumptions. Well, a test that was designed for precisely this situation is the Kruskal-Wallis test which doesn't require these assumptions. It basically replaces the weight gain scores with their rank numbers and tests whether these are equal over groups. We'll run it by following the screenshots below.
Running a Kruskal-Wallis Test in SPSS
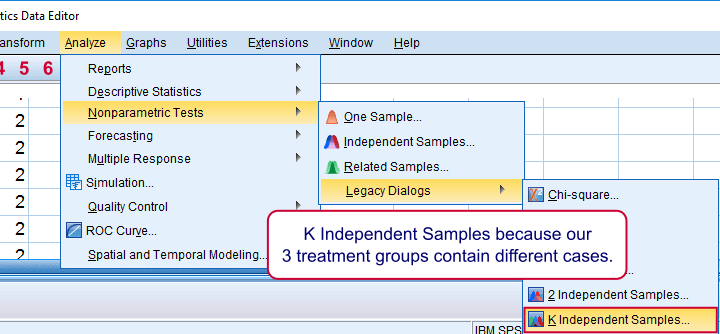
We use if we compare 3 or more groups of cases. They are “independent” because our groups don't overlap (each case belongs to only one creatine condition).
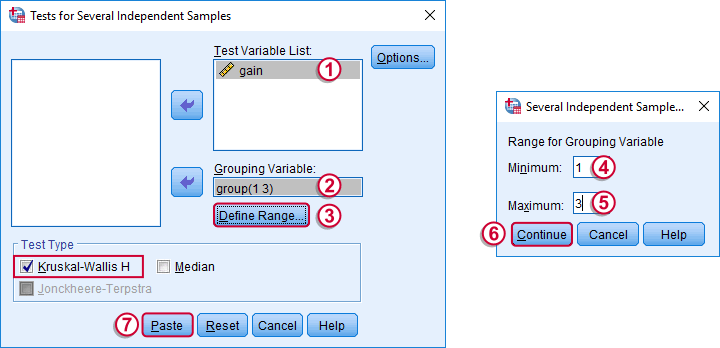
Depending on your license, your SPSS version may or may have the option shown below. It's fine to skip this step otherwise.
SPSS Kruskal-Wallis Test Syntax
Following the previous screenshots results in the syntax below. We'll run it and explain the output.
NPAR TESTS
/K-W=gain BY group(1 3)
/MISSING ANALYSIS.
SPSS Kruskal-Wallis Test Output
We'll skip the “RANKS” table and head over to the “Test Statistics” shown below.
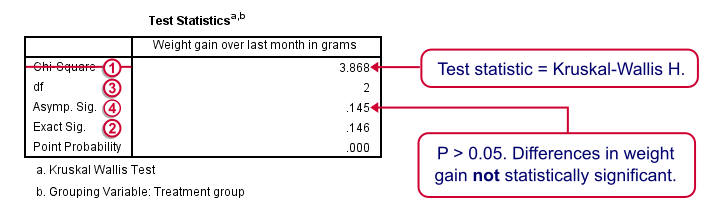
 Our test statistic -incorrectly labeled as “Chi-Square” by SPSS- is known as Kruskal-Wallis H. A larger value indicates larger differences between the groups we're comparing. For our data it's roughly 3.87. We need to know its sampling distribution for evaluating whether this is unusually large.
Our test statistic -incorrectly labeled as “Chi-Square” by SPSS- is known as Kruskal-Wallis H. A larger value indicates larger differences between the groups we're comparing. For our data it's roughly 3.87. We need to know its sampling distribution for evaluating whether this is unusually large.
 Exact Sig. uses the exact (but very complex) sampling distribution of H. However, it turns out that if each group contains 4 or more cases, this exact sampling distribution is almost identical to the (much simpler) chi-square distribution.
Exact Sig. uses the exact (but very complex) sampling distribution of H. However, it turns out that if each group contains 4 or more cases, this exact sampling distribution is almost identical to the (much simpler) chi-square distribution.
 We therefore usually approximate the p-value with a chi-square distribution. If we compare k groups, we have k - 1 degrees of freedom, denoted by df in our output.
We therefore usually approximate the p-value with a chi-square distribution. If we compare k groups, we have k - 1 degrees of freedom, denoted by df in our output.
 Asymp. Sig. is the p-value based on our chi-square approximation. The value of 0.145 basically means there's a 14.5% chance of finding our sample results if creatine doesn't have any effect in the population at large. So if creatine does nothing whatsoever, we have a fair (14.5%) chance of finding such minor weight gain differences just because of random sampling. If p > 0.05, we usually conclude that our differences are not statistically significant.
Asymp. Sig. is the p-value based on our chi-square approximation. The value of 0.145 basically means there's a 14.5% chance of finding our sample results if creatine doesn't have any effect in the population at large. So if creatine does nothing whatsoever, we have a fair (14.5%) chance of finding such minor weight gain differences just because of random sampling. If p > 0.05, we usually conclude that our differences are not statistically significant.
Note that our exact p-value is 0.146 whereas the approximate p-value is 0.145. This supports the claim that H is almost perfectly chi-square distributed.
Kruskal-Wallis Test - Reporting
The official way for reporting our test results includes our chi-square value, df and p as in
“this study did not demonstrate any effect from creatine,
H(2) = 3.87, p = 0.15.”
So that's it for now. I hope you found this tutorial helpful. Please let me know by leaving a comment below. Thanks!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 71 COMMENTS:
By Ha My on November 9th, 2017
Thanks Ruben,
As I mentioned before, my experiment is to test if the changing in soil will effect the plant or not. So when get the result, one pot have a plant that is not germination. SO it means my sample is 6,6,6,and 5. As my teacher said it is possible to use ANOVA one way. BUt when I ran the test , it have 2 results. If i assign the length of death plant as 0 then the result show that it have p0.05. So would test i should do?
By Ruben Geert van den Berg on November 10th, 2017
Hi Ha My!
If some plant does not germinate at all, you could also say "I don't know how the soil would have affected it" and exclude it from analysis. If you assign it zero, you basically assume that it was the soil that killed the plant -zero, really bad soil!
Now the big difference between ANOVA and the KW-test is that ANOVA requires normally distributed variables -preferably with equal variances. With such small sample sizes, it's hard to say if your dependent variable(s) have normal distributions or not so the KW-test is the safer option here.
Many researchers would probably run both -if the ANOVA assumptions don't seem too badly violated. If they yield the same conclusion, you'll have a strong case. If they don't, be open and honest and say that "there some evidence ... but ...". Does that make any sense?
By NUR FAQIHAH BINTI MOHD FAUZI on April 22nd, 2018
does the output on the table explained all the result?
By Ruben Geert van den Berg on April 22nd, 2018
Hi Nur!
Regarding our null hypothesis: yes. We don't reject it. We can't conclude that creatine has any effect in the entire population.
There's also the RANKS table in the output but I left it out. It may be useful for ordinal variables. However, in this example our outcome variable is metric so we can safely report the means table presented in this tutorial.
Hope that helps!
By Erik Skeppner on May 15th, 2018
Hi!
A question! :) If you'd find a significance, wouldn't the test show between which groups it lies or doesn't?