The assumption of equal intervals says that all distances between adjacent answer categories are equal in the repondents’ perception. This assumption is an attempt to justify treating ordinal variables as if they were metric variables. Doing so enables one to compute means, standard deviations and Pearson correlations on ordinal variables. This is simpler than using more appropriate techniques.

Assumption of Equal Intervals - Example

Suppose we have a variable that supposedly measures customer satisfaction with the following answer categories

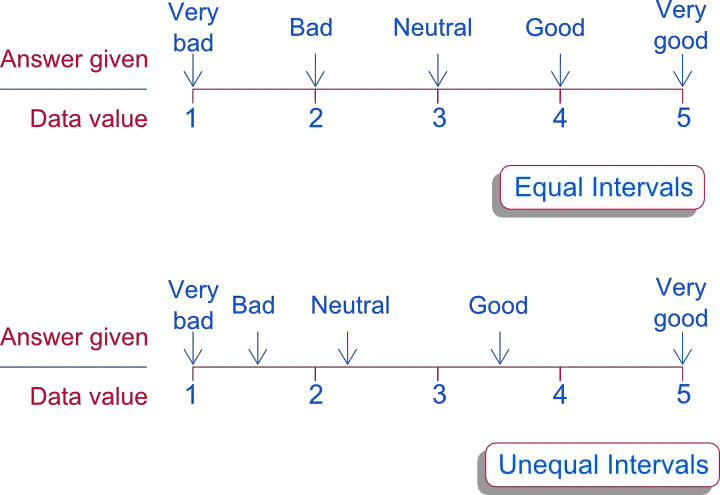
• Very bad (1)
• Bad (2)
• Neutral (3)
• Good (4)
• Very good (5)

Now we have two male respondents scoring 2 and 4 and two female respondents scoring 3 and 3. Now a marketeer wants to know whether men are more or less satisfied than women. But the answer is that we don't know. This is because we don't know the difference between "2: Bad" and "3: Neutral" (or any other answers) in the respondents' perception. 'Perception' does not have any fixed unit of measurement. (Since the order of the answer categories is undisputable, we consider it an ordinal variable.)

Assuming Equal Intervals

If it is assumed that intervals between answers are equal, an ordinal variable is treated as a metric variable. Now we may simply calculate that men scored (2 + 4) / 3 = 3 on average and women as well (3 + 3) / 2 = 3. This answers the 'unanswerable' question from our marketeer. Everybody happy. Or not?

What if the Assumtion Doesn't Hold?

Assumption of Equal Intervals

But what if the intervals are unequal in the respondents' perception? Say the latter is realistically reflected by the following values (see illustration)

• Very bad (1)
• Bad (1.5)
• Neutral (2.25)
• Good (3.5)
• Very good (5)

If this holds, men are actually more satisfied (1.5 + 3.5) / 2 = 2.5 than women (2.25 + 2.25) / 2 = 2.25. So the conclusion drawn earlier was misleading.

Conclusion

According to some academic standards, making the assumption of equal intervals is unsound practice and strictly forbidden. However, in real life research (depending on your field) it may be perfectly common. At least be aware of this controversy and keep in mind what you're doing.