A course was evaluated by 183 students. The data are in course_evaluation.sav, part of which is shown below. The teacher wants to know the average age of his students but we only have their date of birth.

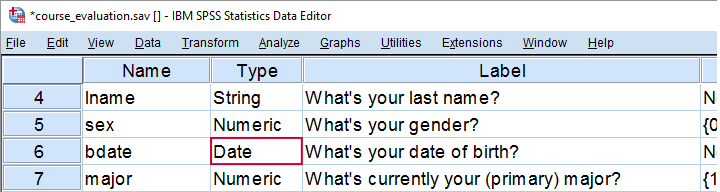
1. Ensure Date of Birth is a Date Variable

The first thing we'll do is check if date of birth is a real date variable. We readily see in variable view that this is the case here. Sometimes dates end up in SPSS as string variables and if so, we first need to convert them to date variables. Some examples for doing so are in Convert String to Date Variable.

2. Choose a Comparison Date

Since (average) age is literally changing every second, we need to answer “age at which point in time?” The most obvious option is age at the moment the data were collected. Such a completion date may be present in your data. If it isn't, we'll make an educated guess.

3. Compute Age with Known Completion Date

Our data hold a variable cdate which contains the completion dates for the questionnaire. We'll now easily compute age with the syntax below and we'll inspect its histogram to make sure the result has a plausible distribution.

Result

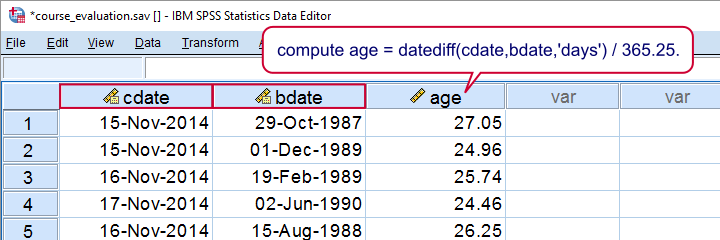
So we basically computed the number of days between date of birth and completion and divided that by 365.25, the average number of days in a year. You may wonder why we don't just use DATEDIFF(cdate,bdate,'years'). We'll get to that in a minute.

4. Compute Age with Unknown Completion Date

If we don't have a completion date in our data, we'll try and make a good guess. Let's say we guess January 1, 2015. We can convert this into an SPSS date value by using date.dmy(1,1,2015) and thus create our guessed completion date as a new variable in our dataset. Alternatively, we may insert this function directly into our age computation formula as shown below.

Days or Years?

So why did we extract days and divide those by 365.25, the average number of days in a year? The simple reason is that SPSS truncates the outcome of DATEDIFF. This means that someone who is 20 years and 364 days old will be assigned an age of 20.00 years, which is almost an entire year off.

Result

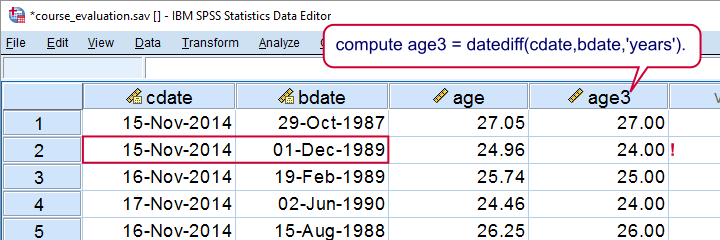
This probably convinces you that extracting years directly is not a good idea: on average, we'll underestimate age by half a year by doing so.For the sake of simplicity, we'll assume that birthdays are uniformly distributed over the year, which I believe roughly holds.

Final Notes

If you don't want to see any decimal places, your best option is probably running formats age (f3). which will display all ages as integers. Alternatively, if you want ages to be integers, you could run compute age = rnd(age). but this obviously introduces some error -bad but not quite as bad as the aforementioned bias.

It guess that's about it. I hope you found this tutorial helpful. Thanks for reading!