• Summary
• Mahalanobis Distances - Basic Reasoning
• Mahalanobis Distances - Formula and Properties
• Finding Mahalanobis Distances in SPSS
• Critical Values Table for Mahalanobis Distances
• Mahalanobis Distances & Missing Values

Summary

In SPSS, you can compute (squared) Mahalanobis distances as a new variable in your data file. For doing so, navigate to Analyze Regression Linear and open the “Save” subdialog as shown below.

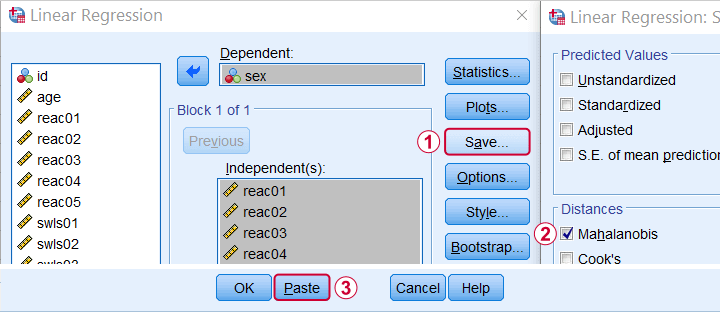
Keep in mind here that Mahalanobis distances are computed only over the independent variables. The dependent variable does not affect them unless it has any missing values. In this case, the situation becomes rather complicated as I'll cover near the end of this article.

Mahalanobis Distances - Basic Reasoning

Before analyzing any data, we first need to know if they're even plausible in the first place. One aspect of doing so is checking for outliers: observations that are substantially different from the other observations. One approach here is to inspect each variable separately and the main options for doing so are

• inspecting histograms;
• inspecting boxplots or
• inspecting z-scores.

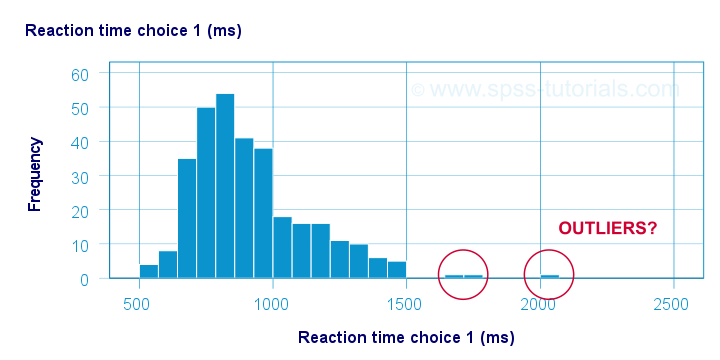
Now, when analyzing multiple variables simultaneously, a better alternative is to check for multivariate outliers: combinations of scores on 2(+) variables that are extreme or unusual. Precisely how extreme or unusual a combination of scores is, is usually quantified by their Mahalanobis distance.

The basic idea here is to add up how much each score differs from the mean while taking into account the (Pearson) correlations among the variables. So why is that a good idea? Well, let's first take a look at the scatterplot below, showing 2 positively correlated variables.

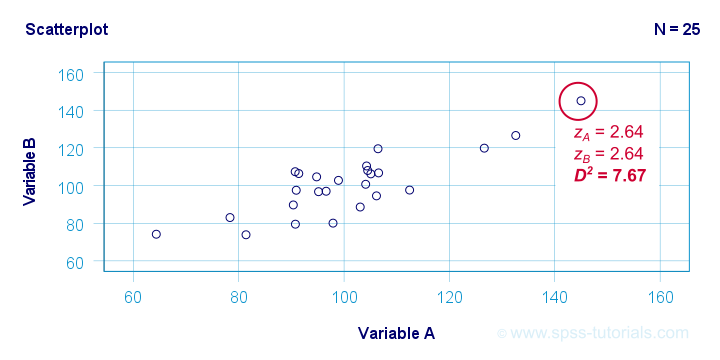
The highlighted observation has rather high z-scores on both variables. However, this makes sense: a positive correlation means that cases scoring high on one variable tend to score high on the other variable too. The (squared) Mahalanobis distance D² = 7.67 and this is well within a normal range.

So let's now compare this to the second scatterplot shown below.

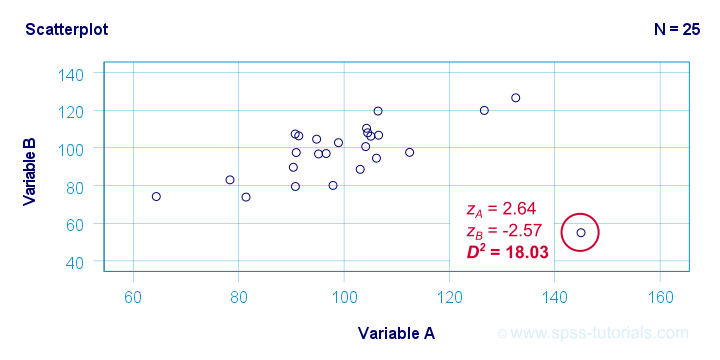
The highlighted observation has a rather high z-score on variable A but a rather low one on variable B. This is highly unusual for variables that are positively correlated. Therefore, this observation is a clear multivariate outlier because its (squared) Mahalanobis distance D² = 18.03, p < .0005. Two final points on these scatterplots are the following:

• the (univariate) z-scores fail to detect that the highlighted observation in the second scatterplot is highly unusual;
• this observation has a huge impact on the correlation between the variables and is thus an influential data point. Again, this is detected by the (squared) Mahalanobis distance but not by z-scores, histograms or even boxplots.

Mahalanobis Distances - Formula and Properties

Software for applied data analysis (including SPSS) usually computes squared Mahalanobis distances as

\(D^2_i = (\mathbf{x_i} - \mathbf{\overline{x}})'\;\mathbf{S}^{-1}\;(\mathbf{x_i} - \overline{\mathbf{x}})\)

where

• \(D^2\) denotes the squared Mahalanobis distance for case \(i\);
• \(\mathbf{x_i}\) denotes the vector of scores for case \(i\);
• \(\mathbf{\overline{x}}\) denotes the vector of means (centroid) over all cases;
• \(S\) denotes the covariance matrix over all variables.

Some basic properties are that

• Mahalanobis distances can (theoretically) range from zero to infinity;
• Mahalanobis distances are standardized: they are scale independent so they are unaffected by any linear transformations to the variables they're computed on;
• Mahalanobis distances for a single variable are equal to z-scores;
• squared Mahalanobis distances computed over k variables follow a χ²-distribution with df = k under the assumption of multivariate normality.

Finding Mahalanobis Distances in SPSS

In SPSS, you can use the linear regression dialogs to compute squared Mahalanobis distances as a new variable in your data file. For doing so, navigate to Analyze Regression Linear and open the “Save” subdialog as shown below.

Again, Mahalanobis distances are computed only over the independent variables. Although this is in line with most text books, it makes more sense to me to include the dependent variable as well. You could do so by

• adding the actual dependent variable to the independent variables and
• temporarily using an alternative dependent variable that is neither a constant, nor has any missing values.

Finally, if you've any missing values on either the dependent or any of the independent variables, things get rather complicated. I'll discuss the details at the end of this article.

Critical Values Table for Mahalanobis Distances

After computing and inspecting (squared) Mahalanobis distances, you may wonder: how large is too large? Sadly, there's no simples rule of thumb here but most text books suggest that (squared) Mahalanobis distances for which p < .001 are suspicious for reasonable sample sizes. Since p also depends on the number of variables involved, we created a handy overview table in this Googlesheet, partly shown below.

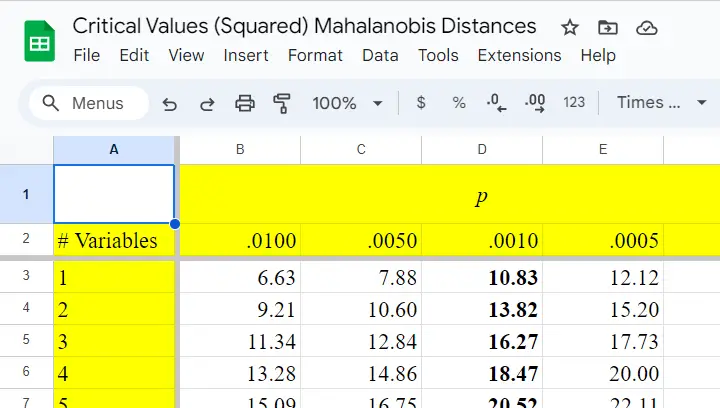
Mahalanobis Distances & Missing Values

Missing values on either the dependent or any of the independent variables may affect Mahalanobis distances. Precisely when and how depends on which option you choose for handling missing values in the linear regression dialogs as shown below.

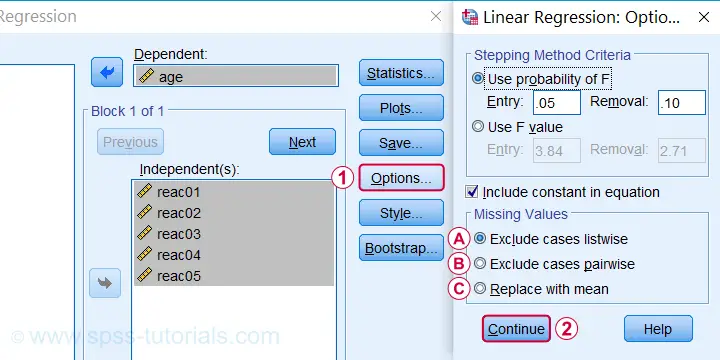
If you select listwise exclusion,

• Mahalanobis distances are computed for all cases that have zero missing values on the independent variables;
• missing values on the dependent variable may affect the Mahalanobis distances. This is because these are based on the listwise complete covariance matrix over the dependent as well as the independent variables.

If you select pairwise exclusion,

• Mahalanobis distances are computed for all cases that have zero missing values on the independent variables;
• missing values on the dependent variable do not affect the Mahalanobis distances in any way.

If you select replace with mean,

• missing values on the dependent and independent variables are replaced with the (variable) means before SPSS proceeds with any further computations;
• Mahalanobis distances are computed for all cases, regardless any missing values;
• \(D^2\) = 0 for cases having missing values on all independent variables. This makes sense because \(\mathbf{x_i} - \mathbf{\overline{x}}\) results in a vector of zeroes after replacing all missing values by means.

References

• Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
• Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.
• Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition). New York: Routledge.
• Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
• Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
• Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.