In SPSS, SUM(v1,v2) is not always equivalent to v1 + v2. This tutorial explains the difference and shows how to make the right choice here.

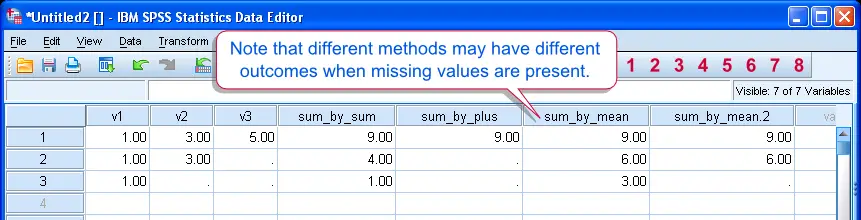Different Ways of Taking Sums have Different Outcomes when Missing Values are Present

Explanation

• In SPSS, v1 + v2 + v3 will result in a system missing value if at least one missing value is present in v1, v2 or v3.
• The first alternative, SUM(v1, v2, v3) implicitly replaces missing values with zeroes.
• The second alternative, MEAN(v1, v2, v3) * 3 implicitly replaces missing values with the mean of the non missing values.
• The third alternative, MEAN.2(v1, v2, v3) * 3 is almost similar to the second. However, by suffixing MEAN by .2, you ensure that a mean is only calculated if at least two non missing values are present in v1, v2 and v3.
• These points are demonstrated by the syntax below.

SPSS Syntax Demonstration

So Which one Is Best?

• This question is rather hard to answer. It may depend on the meaning of the missing values (question skipped? technical problem?). Also, what are the individual questions and the sum supposed to reflect?
• Second, the amount of missing values and sample size may be taken into account. Does it permit excluding some observations with missing values? Will this affect representativity and if so, is that a real problem?
• For one thing, sums calculated by SUM may be biased towards zero. For instance, if v1 through v3 measure components of satisfaction, respondents will be seen as "less satisfied" insofar they have more missing values. That conclusion may be misleading.
• Using the + operator does not induce such bias but may result in many missing values in the sum. This problem becomes larger as more missing values are present in the input variables and a sum is taken over more variables.
• Multiplying the mean by the number of variables, may be a better alternative. However, it will always come up with a sum if there's at least one non missing value. Especially with many input variables, a single value may be jugded insufficient for inferring a summation measure.
• But perhaps none of these options is expected to yield sufficiently accurate results. In this case, one could partly circumvent the problem with a (multiple) imputation of missing values.