For running a binomial test in SPSS, see SPSS Binomial Test.

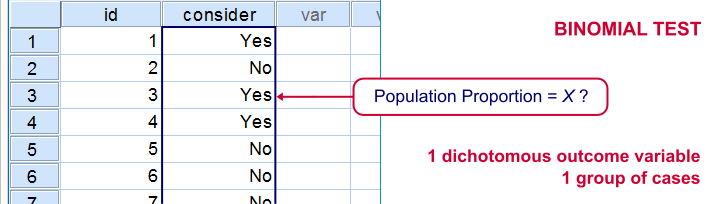
A binomial test examines if some
population proportion is likely to be x. For example, is 50% -a proportion of 0.50- of the entire Dutch population familiar with my brand? We asked a simple random sample of N = 10 people if they are. Only 2 of those -a proportion of 0.2- or 20% know my brand. Does this sample proportion of 0.2 mean that the population proportion is not 0.5? Or is 2 out of 10 a pretty normal outcome if 50% of my population really does know my brand?
The binomial test is the simplest statistical test there is. Understanding how it works is pretty easy and will help you understand other statistical significance tests more easily too. So how does it work?

Binomial Test - Basic Idea

If the population proportion really is 0.5, we can find a sample proportion of 0.2. However, if the population proportion is only 0.1 (only 10% of all Dutch adults know the brand), then we may also find a sample proportion of 0.2. Or 0.9. Or basically any number between 0 and 1. The figure below illustrates the basic problem -I mean challenge- here.

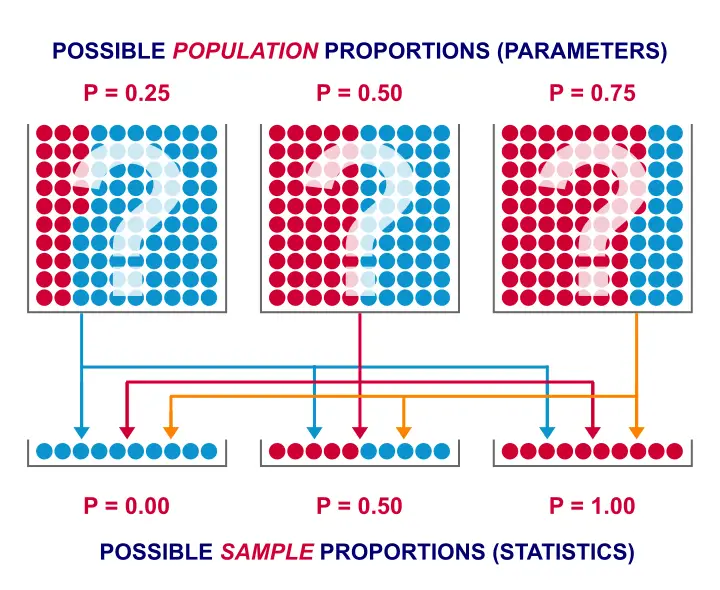Will the real population proportion please stand up now??

So how can we conclude anything at all about our population based on just a sample? Well, we first make an initial guess about the population proportion which we call the null hypothesis: a population proportion of 0.5 knows my brand.
Given this hypothesis, many sample proportions are possible. However, some outcomes are extremely unlikely or almost impossible. If we do find an outcome that's almost impossible given some hypothesis, then the hypothesis was probably wrong: we conclude that the population proportion wasn't x after all.
So that's how we draw population conclusions based on sample outcomes. Basically all statistical tests follow this line of reasoning. The basic question for now is: what's the probability of finding 2 successes in a sample of 10 if the population proportion is 0.5?

Binomial Test Assumptions

First off, we need to assume independent observations. This basically means that the answer given by any respondent must be independent of the answer given by any other respondent. This assumption (required by almost all statistical tests) has been met by our data.

Binomial Distribution - Formula

If 50% of some population knows my brand and I ask 10 people, then my sample could hold anything between 0 and 10 successes. Each of these 11 possible outcomes and their associated probabilities are an example of a binomial distribution, which is defined as $$P(B = k) = \binom{n}{k} p^k (1 - p)^{n - k}$$ where

• \(n\) is the number of trials (sample size);
• \(k\) is the number of successes;
• \(p\) is the probability of success for a single trial or the (hypothesized) population proportion.

Note that \(\binom{n}{k}\) is a shorthand for \(\frac{n!}{k!(n - k)!}\) where \(!\) indicates a factorial.

For practical purposes, we get our probabilities straight from Google Sheets (it uses the aforementioned formula under the hood but it doesn't bother us with it).

Binomial Distribution - Chart

Right, so we got the probabilities for our 11 possible outcomes (0 through 10 successes) and visualized them below.

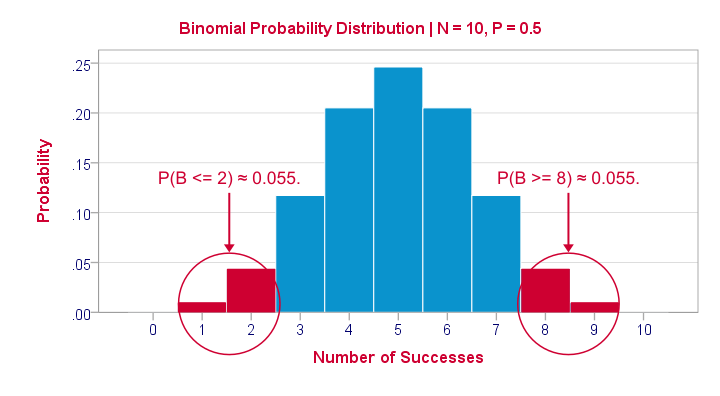
If a population proportion is 0.5 and we sample 10 observations, the most likely outcome is 5 successes: P(B = 5) ≈ 0.24. Either 4 or 6 successes are also likely outcomes (P ≈ 0.2 for each).
The probability of finding 2 or fewer successes -like we did- is 0.055. This is our one-sided p-value.
Now, very low or very high numbers of successes are both unlikely outcomes and should both cast doubt on our null hypothesis. We therefore take into account the p-value for the opposite outcome -8 or more successes- which is another 0.055. Like so, we find a 2-sided p-value of 0.11. If we would draw 1,000 samples instead of just 1, then some 11% of those should result in 2(-) or 8(+) successes when the population proportion is 0.5. Our sample outcome should occur in a reasonable percentage of samples. And since 11% is not very unlikely, our sample does not refute our hypothesis that 50% of our population knows our brand.

Binomial Test - Google Sheets

We ran our example in this simple Google Sheet. It's accessible to anybody so feel free to take a look at it.

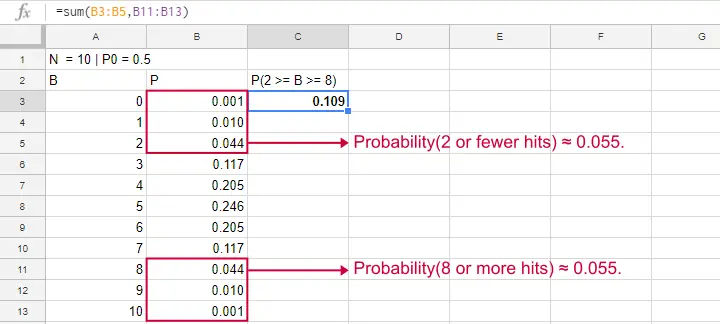
Binomial Test - SPSS

Perhaps the easiest way to run a binomial test is in SPSS - for a nice tutorial, try SPSS Binomial Test. The figure below shows the output for our current example. It obviously returns the same p-value of 0.109 as our Google Sheet.

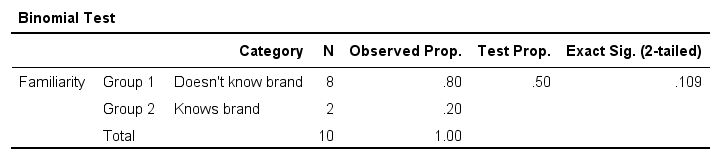
Note that SPSS refers to p as “Exact Sig. (2-tailed)”. Is there a non exact p-value too then? Well, sort of. Let's see how that works.

Binomial Test or Z Test?

Let's take another look at the binomial probability distribution we saw earlier. It kinda resembles a normal distribution. Not convinced? Take a look at the binomial distribution below.

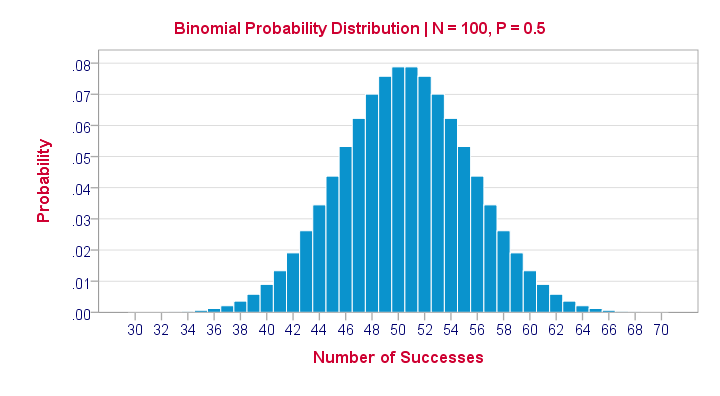
For a sample of N = 100, our binomial distribution is virtually identical to a normal distribution. This is caused by the central limit theorem. A consequence is that -for a larger sample size- a z-test for one proportion (using a standard normal distribution) will yield almost identical p-values as our binomial test (using a binomial distribution).

But why would we prefer a z-test over a binomial test?

• We can always use a 2-sided z-test. However, a binomial test is always 1-sided unless P₀ = 0.5.
• A z-test allows us to compute a confidence interval for our sample proportion.
• We can easily estimate statistical power for a z-test but not for a binomial test.
• A z-test is computationally less heavy, especially for larger sample sizes.I suspect that most software actually reports a z-test as if it were a binomial test for larger sample sizes.

So when can we use a z-test instead of a binomial test? A rule of thumb is that P₀*n and (1 - P₀)*n must both be > 5, where P₀ denotes the hypothesized population proportion and n the sample size.

So that's about it regarding the binomial test. I hope you found this tutorial helpful. Thanks for reading!