The table below presents a quick overview of functions and operators in SPSS, sorted by type (numeric, string, ...). Details and examples for some lesser known functions are covered below the table.
| TYPE | Function | DESCRIPTION | EXAMPLE |
|---|---|---|---|
| Comparison | = (or EQ) | Equal to | if(var01 = 0) var02 = 1. |
| Comparison | <> (or NE) | Not equal to | if(var01 <> 0) var02 = 1. |
| Comparison | < (or LT) | Less than | if(var01 < 0) var02 = 1. |
| Comparison | <= (or LE) | At most | if(var01 <= 0) var02 = 1. |
| Comparison | > (or GT) | Greater than | if(var01 > 0) var02 = 1. |
| Comparison | >= (or GE) | At least | if(var01 >= 0) var02 = 1. |
| Comparison | RANGE | Within range | if(range(score,0,20) grp01 = 1. |
| Comparison | ANY | First value among second, third, ... values? | if(any(nation,1,3,5)) flag01 = 1. |
| Logical | & (or AND) | All arguments true? | if(sex = 0 & score >= 100) grp01 = 1. |
| Logical | | (or OR) | At least 1 argument true? | if(sex = 0 | score <= 90) grp01 = 1. |
| Logical | NOT | Argument not true | select if(not(missing(score))). |
| Numeric | + | Addition | compute sum01 = var01 + var02. |
| Numeric | - | Subtraction | compute dif01 = var01 - var02. |
| Numeric | * | Multiplication | compute revenue = sales * price. |
| Numeric | / | Division | compute avg01 = sum01 / trials. |
| Numeric | ** | Exponentiation | compute square01 = var01**2. |
| Numeric | SQRT | Square root | compute root01 = sqrt(var01). |
| Numeric | RND | Round | compute score = rnd(reactime). |
| Numeric | MOD | Modulo Function | compute cntr = mod(id,4). |
| Numeric | TRUNC | Truncate | compute score = trunc(reactime). |
| Numeric | ABS | Absolute value | compute abs01 = abs(score). |
| Numeric | EXP | Exponential Function | compute escore = exp(score). |
| Numeric | LN | Natural logarithm | compute lnscore = ln(score). |
| Statistical | MIN | Minimum over variables | compute min01 = min(var01 to var10). |
| Statistical | MAX | Maximum over variables | compute max01 = max(var01 to var10). |
| Statistical | SUM | Sum over variables | compute total = sum(var01 to var10). |
| Statistical | MEAN | Mean over variables | compute m01 = mean(var01 to var10). |
| Statistical | MEDIAN | Median over variables | compute me01 = median(var01 to var10). |
| Statistical | VARIANCE | Variance over variables | compute vnc01 = variance(var01 to var10). |
| Statistical | SD | Standard deviation over variables | compute sd01 = sd(var01 to var10). |
| Missing | MISSING | System or user missing | select if(missing(score)). |
| Missing | SYSMIS | System missing | select if(not(sysmis(score))). |
| Missing | NMISS | Count missing values over variables | compute mis01 = nmiss(v01 to v10). |
| Missing | NVALID | Count valid values over variables | compute val01 = nvalid(v01 to v10). |
| String | LOWER | Convert to lowercase | compute sku = lower(sku). |
| String | UPCASE | Convert to uppercase | compute sku = upcase(sku). |
| String | CHAR.LENGTH | Number of characters in string | compute len01 = char.length(firstname). |
| String | CHAR.INDEX | Position of first occurrence of substring | compute pos01 = char.index('banana','a'). |
| String | CHAR.RINDEX | Position of last occurrence of substring | compute pos02 = char.rindex('banana','a'). |
| String | CHAR.SUBSTR | Extract substring | compute firstchar = char.substr(name,1,1). |
| String | CONCAT | Concatenate strings | compute name = concat(fname,' ',lname). |
| String | REPLACE | Replace substring | compute str01 = replace('dog','g','t'). |
| String | RTRIM | Right trim string | compute str02 = rtrim(str02). |
| String | LTRIM | Left trim string | compute str03 = ltrim(str03). |
| Date | DATE.DMY | Convert day, month, year into date | compute mydate = date.dmy(31,1,2024). |
| Date | DATEDIFF | Compute difference between dates in chosen time units | compute age = datediff(datevar02,datevar01,'years'). |
| Date | DATESUM | Add time units to date | compute followup = datesum(datevar01,100,'days'). |
| Date | XDATE | Extract date component from date | compute byear = xdate.year(bdate). |
| Time | TIME.HMS | Convert hours, minutes, seconds into time | compute time01 = time.hms(17,45,12). |
| Distribution | CDF | Cumulative probability distribution or density Function | compute pvalue = cdf.normal(-1.96,0,1). |
| Distribution | IDF | Inverse probability distribution or density Function | compute zvalue95 = idf.normal(.025,0,1). |
| Distribution | Probability distribution or density Function | compute prob = pdf.binom(0,10,.5). | |
| Distribution | RV | Draw (pseudo) random numbers from specified probability distribution or density Function | compute rand01 = rv.uniform(0,1). |
| Other | LAG | Retrieve value from previous case | compute prev = lag(varname). |
| Other | NUMBER | Convert string to number | compute nvar = number(svar,f3). |
| Other | STRING | Convert number to string | compute svar = string(nvar,f3). |
| Other | VALUELABEL | Set value labels as string values | compute svar = valuelabel(nvar). |
SPSS ANY Function Example
In SPSS, ANY evaluates if the first value is among the second, third, ... values. So for example, let's say we want to know if the completion day was a Monday, Wednesday or a Friday? We could use if(cday = 2 or cday = 4 or cday = 6) flag01 = 1. However, a nice shorthand here is if(any(cday,2,4,6)) flag01 = 1. The screenshot below shows the result when run on spss-functions.sav.
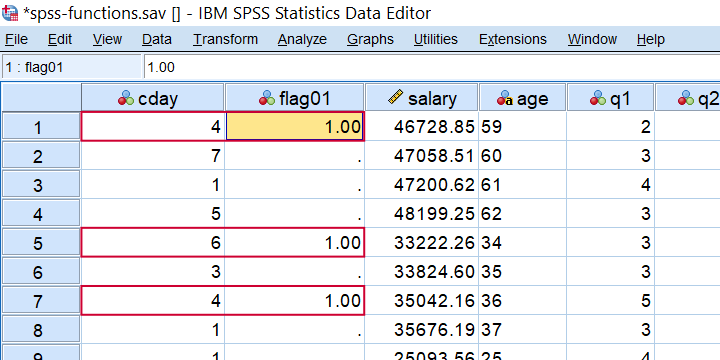 Result of IF(ANY(CDAY,2,4,6)) FLAG01 = 1.
Result of IF(ANY(CDAY,2,4,6)) FLAG01 = 1.
As a second example, let's flag all cases who scored at least one 1 among the last 5 variables. This is often done with COUNT and then RECODE but a shorter option is if(any(1,q1 to q5)) flag02 = 1. which checks if the value 1 is among variables q1 to q5.
SPSS RND Function Example
In SPSS, you can round a value x to some constant c which is 1 by default. Like so,
RND(123456.789) = 123457RND(123456.789,10) = 123460 andRND(123456.789,.1) = 123456.8.
So for rounding salaries to dollars, you could use compute salary = rnd(salary). Alternatively, use compute salary = rnd(salary,.01). for rounding to dollar cents. For rounding salaries to thousands of dollars, use compute salary = rnd(salary,1000). as shown below when run on spss-functions.sav.
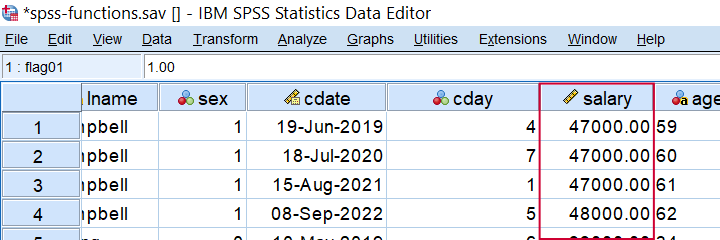 Result of COMPUTE SALARY = RND(SALARY,1000).
Result of COMPUTE SALARY = RND(SALARY,1000).
SPSS MOD Function Example
In SPSS, MOD is short for the modulo function where MOD(X,Y) returns the remainder of X after subtracting Y from it as many times as possible. This comes in handy for creating a trial counter if each respondent has the same number of trials as in compute trial = mod(($casenum - 1),4) + 1. When run on spss-functions.sav, the result is shown below.
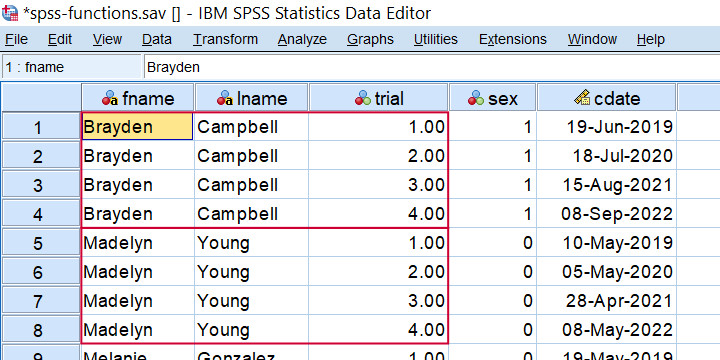 Trial counter created by COMPUTE TRIAL = MOD(($CASENUM - 1),4) + 1.
Trial counter created by COMPUTE TRIAL = MOD(($CASENUM - 1),4) + 1.
SPSS TRUNC Function Example
In SPSS, you can truncate (“round down”) a value x to some constant c which is 1 by default. Like so,
- TRUNC(123456.789) = 123456
- TRUNC(123456.789,10) = 123450 and
- TRUNC(123456.789,.1) = 123456.7.
TRUNC comes in handy for creating a respondent identifier if each respondent has the same number of trials as in compute respid = trunc(($casenum - 1) / 4) + 1. The result is shown below when run on spss-functions.sav.
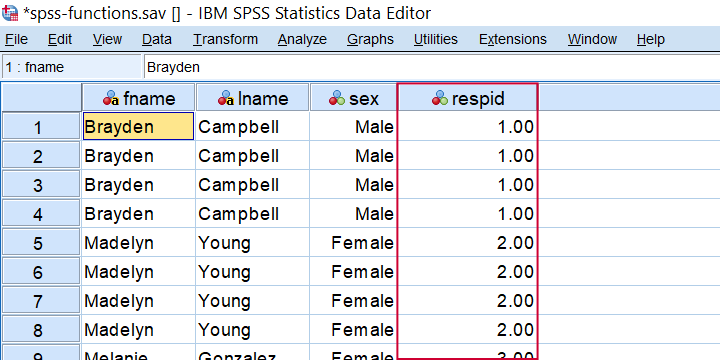 Result from COMPUTE RESPID = TRUNC(($CASENUM - 1) / 4) + 1.
Result from COMPUTE RESPID = TRUNC(($CASENUM - 1) / 4) + 1.
SPSS MEAN Function Example
In SPSS, MEAN is pretty straightforward but there's 2 things you should know: first off, if there's any missing values, then
$$mean = \frac{sum(valid\;values)}{number\;of\;valid\;values}$$
This is important because the number of valid values may differ over respondents.
Second, you can restrict MEAN to a minimal number of valid values, k, by using MEAN.k(...). So for spss-functions.sav, compute m01 = mean.5(q1 to q5). only computes mean scores over cases not having any missing values over these 5 variables as shown below.
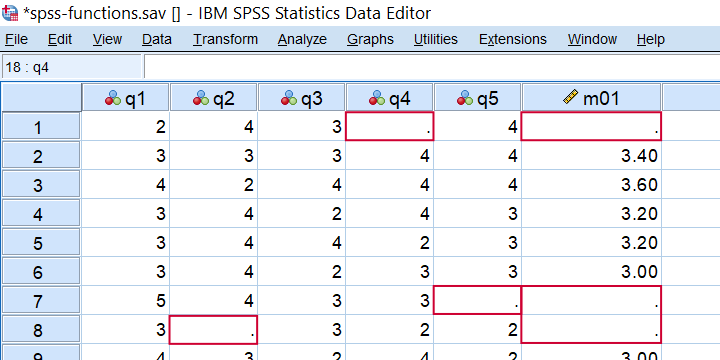 Result from COMPUTE M01 = MEAN.5(Q1 TO Q5).
Result from COMPUTE M01 = MEAN.5(Q1 TO Q5).
SPSS SD Function Example
In SPSS, SD computes the standard deviation over variables. It has the same properties discussed for MEAN. SD comes in handy for detecting “straightliners” (respondents giving the same answer to all or most questions). Like so, compute sd01 = sd(q1 to q5). quickly does the job for spss-functions.sav.
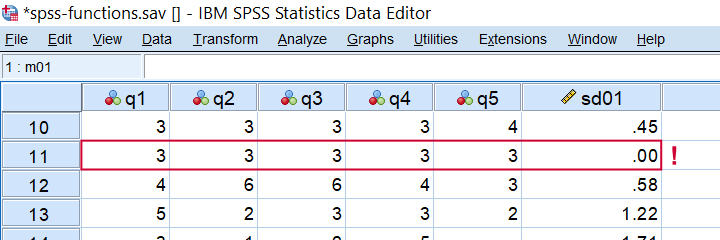 Detecting straightliners with COMPUTE SD01 = SD(Q1 TO Q5).
Detecting straightliners with COMPUTE SD01 = SD(Q1 TO Q5).
SPSS CDF Function Example
CDF is short for cumulative (probability) density (or distribution) function: it returns $$P(X \le x)$$,
given some probability density function. For example, assuming that z follows a standard normal distribution,
what's the 2-tailed p-value for z = -2.0?
We can find this out by running
compute pvalue = 2 * cdf.normal(-2,0,1).
as shown below.
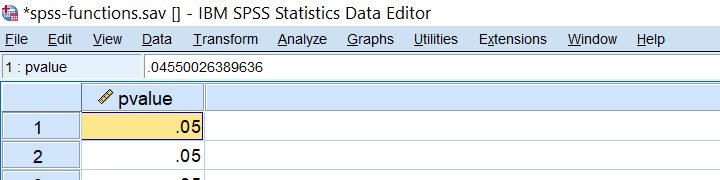
SPSS IDF Function Example
IDF is short for inverse (probability) density (or distribution) function: it returns a critical value for some chosen probability, given a density function. Note that this is exactly what we do when computing confidence intervals. For example: which z-value has a cumulative probability of .025? Well, we can compute this by compute zcrit = idf.normal(.025,0,1). as shown below.
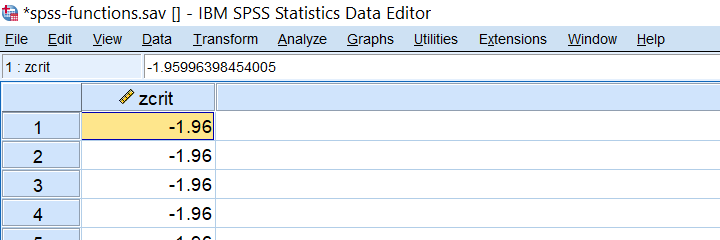
SPSS NUMBER Function Example
In SPSS, NUMBER converts a string variable into a (new) numeric one. With regard to spss-functions.sav, compute nage = number(age,f2). creates a numeric age variable based on the string variable containing age.
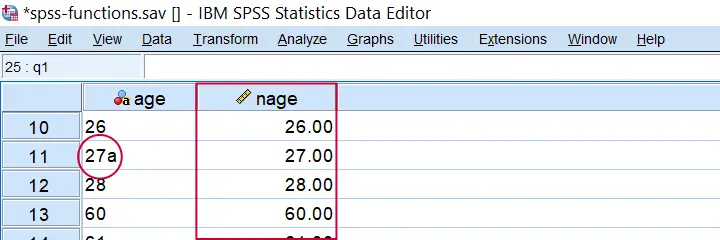 Result from COMPUTE NAGE = NUMBER(AGE,F2). Note the illegal character for case 11.
Result from COMPUTE NAGE = NUMBER(AGE,F2). Note the illegal character for case 11.
Importantly, choosing the f2 format results in SPSS ignoring all but the first 2 characters. If we choose f3 instead as in compute nage = number(age,f3). then SPSS throws the following warning:
>An invalid numeric field has been found. The result has been set to the
>system-missing value.
>Command line: 117 Current case: 11 Current splitfile group: 1
>Field contents: '27a'
This is because the age for case 11 contains an illegal character, resulting in a system missing value. Sadly, when converting this variable with ALTER TYPE,
this value simply disappears from your data
without any warning or error.
In our opinion, this really is a major stupidity in SPSS and very tricky indeed.
SPSS VALUELABEL Function Example
The VALUELABEL function sets the value labels for some variable as the values for some string variable. The syntax below illustrates how it's done for spss-functions.sav.
string sday(a10).
*SET VALUE LABELS FOR CDAY AS VALUES.
compute sday = valuelabel(cday).
execute.
Result
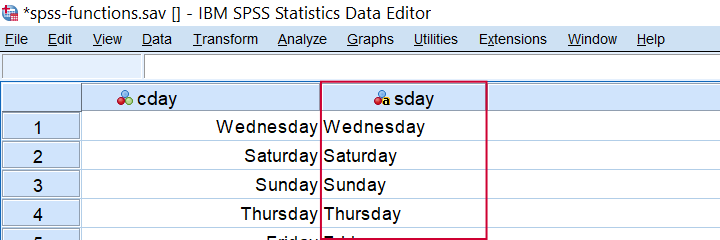 Result from COMPUTE SDAY = VALUELABEL(CDAY).
Result from COMPUTE SDAY = VALUELABEL(CDAY).
Final Notes
Now honestly, our overview of SPSS operators and functions is not 100% comprehensive. I did leave out some examples that are so rare that covering them mostly just clutters up the table without helping anybody.
If you've any questions or remarks, please leave a comment below. And other than that:
thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS