Popular statistical procedures such as ANOVA, a chi-square test or a t-test quietly rely on the assumption that your data are a simple random sample from your population. Violation of this assumption may result in biased or even nonsensical test results and few researchers seem to be aware of this.
Plenty of reasons for a brief discussion of simple random sampling: what exactly is it and why is it so important?

Simple Random Sampling - Definition

Simple random sampling is sampling where each time we sample a unit, the chance of being sampled is the same for each unit in a population. Note that this is a somewhat loose, non technical definition. We'll now use an example to make clear what exactly we mean by this definition.

Simple Random Sampling with Replacement - Example

A textbook example of simple random sampling is sampling a marble from a vase. We record one or more of its properties (perhaps its color, number or weight) and put it back into the vase. We repeat this procedure n times for drawing a sample of size n. The idea is illustrated by the figure below.

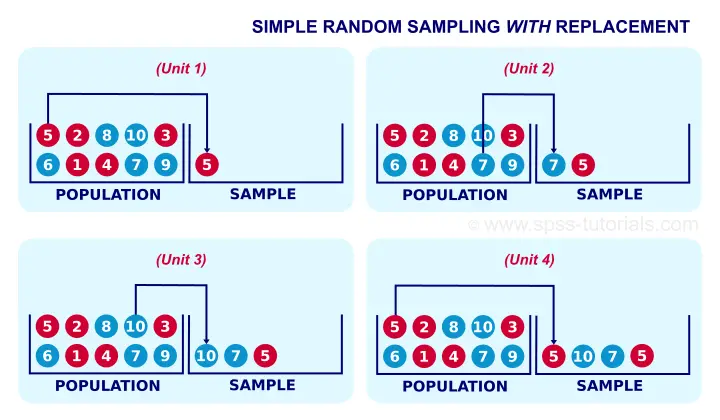
When sampling the first marble, each marble has the same chance of 0.1 of being sampled. When sampling the second marble, each marble still has a 0.1 chance of being sampled. This generalizes to all subsequent marbles being sampled. Each time we sample a unit, all units have similar chances of being sampled. This is precisely what we meant with our definition of simple random sampling.

Simple Random Sampling without Replacement

If you took a good look at the figure, it may surprise you that marble 5 occurs twice in our sample. This may happen because we need to replace each marble we sampled.
Not replacing the marbles we sampled results in simple random sampling without replacement, often abbreviated to SRSWOR. SRSWOR violates simple random sampling. Let's see how that works.

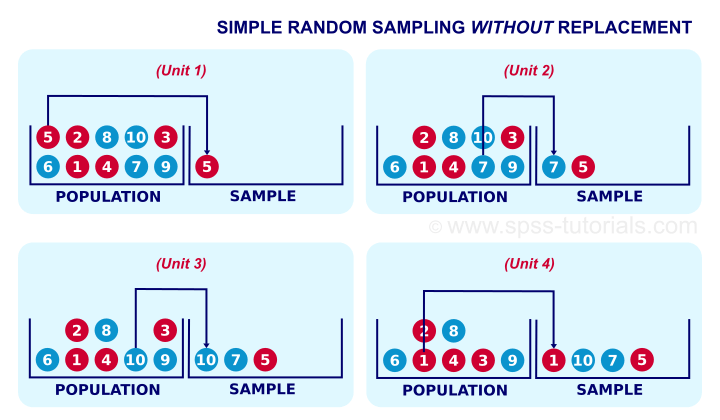
Right, for the first marble we sample, each marble has a 0.1 chance of being sampled. So far, so good. If we don't replace it before sampling a second unit, however, the first unit we sampled has a zero chance of being sampled. The other 9 units each have a chance of 1 in 9 = 0.11 of being sampled as the second unit. This is how SRSWOR violates our definition of simple random sampling. Note that this violation gets worse as we sample more units from a smaller population.

SRSWOR - How Bad Is It?

If you think about the example with the marbles, you'll probably see that it doesn't translate nicely to some real world situations. Most prominently, if we survey a population of people, SRS may result in persons receiving the same questionnaire multiple times. Since this is obviously a bad idea, SRSWOR is usually preferred over simple random sampling here.
SRSWOR is different from simple random sampling necessary for most standard statistical tests. So how serious is this problem? Well, this discussion really deserves a tutorial of its own. Very briefly, however, the problem gets less serious as we sample fewer units from a larger population; when sampling 4 marbles out of 1,000 (instead of 10) marbles, SRSWOR is almost identical to simple random sampling.
A very basic rule of thumb is that bias from using SRSWOR can be neglected when the sample size is less than 10% of the population size. If this doesn't hold, then a finity correction is in place.

Simple Random Sampling - IID Assumption

So far, we discussed what simple random sampling is. But why is it so important? The first reason is that simple random sampling satisfies the IID assumption: independent and identically distributed variables.We're currently working on a tutorial that thoroughly explains the meaning and the importance of this assumption. This assumption -really deserving a tutorial of its own- is the single most important assumption for common statistical procedures.

Simple Random Sampling - Representativity

The second reason why simple random sampling is highly desirable is that it tends to result in samples that are representative for the populations from which they were drawn on all imaginable variables. This very nice feature -driven by the law of large numbers- becomes more apparent with increasing sample sizes.

What if Simple Random Sampling Doesn't Hold?

Good question. Three common sampling procedures that violate simple random sampling are

sampling more than some 10% of a (finite) population;
stratified random sampling;
cluster sampling.

Using (a combination of) these sampling methods results in biased test results. Whether such bias is negligible can't be stated a priori. Formulas are available for correcting for it but actually using them may prove tedious. For SPSS users, these correction formulas have been implemented in SPSS Complex Samples, a somewhat costly add-on module.
Some sampling procedures are not well defined, most notably “convenience sampling”. The amount of bias resulting from such procedures will often remain unknown. This implies that generalizing such results to larger populations is speculative -at best.

Simple Random Sampling - Final Note

Purely statistically, simple random sampling is usually the ideal sampling procedure. Unfortunately, simple random sampling in the social sciences is rare. The reasons for this are discussed in Survey Sampling - How Does It Work?