When it's not feasible to study an entire target population, a simple random sample is the next best option; with sufficient sample size, it satisfies the assumption of independent and identically distributed variables. And perhaps even more important, it will tend to be nicely representative for the population with regard to all variables.

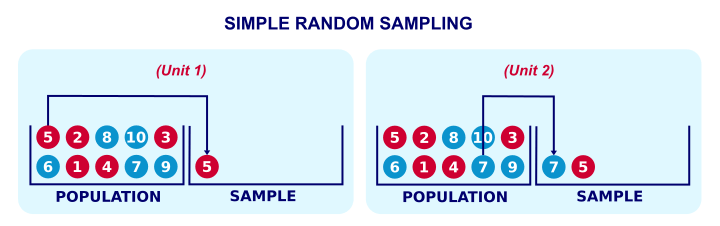
Although simple random sampling nicely satisfies two major statistical assumptions, we rarely see it in practice. This tutorial explains the reasons for this discrepancy. Before discussing the steps in a typical survey sampling procedure, we'll first give a quick overview of the process.

Survey Sampling - Quick Overview

Survey Sampling - The Sampling Frame

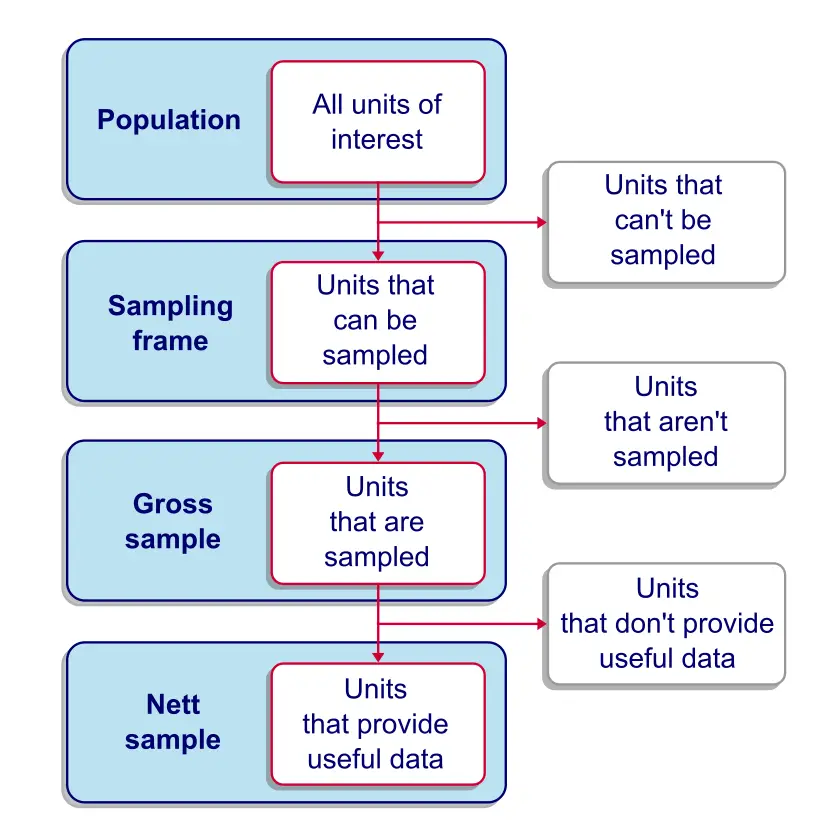
The sampling frame is the collection of units
that are available for our sampling procedure. So what do we mean by that? Well, in many cases a substantial part of our population simply cannot be sampled due to practical reasons. Regarding a target population of people, we rarely have accurate contact information from each single person. If we want to conduct an online survey, then people whose contact information is absent or incorrect have a zero chance of ending up in our sample. For this case, the sampling frame consists of the people in our population whose contact information is available and correct.
A sampling frame we encounter a lot in practice is an (online) panel; commercial research agencies often maintain a database of people who are willing to participate in surveys on a regular basis. When drawing a sample from such a panel, people who don't participate in the panel have a zero chance of ending up in our sample.

Survey Sampling - Coverage

Coverage is the percentage of a target population
that's covered in the sampling frame. For example, the Dutch government has the correct home addresses of almost all Dutch citizens because people are enforced by law to provide this information. If we'd have access to this database, we could draw a random sample from it. In this case, the database would be our sampling frame with a coverage perhaps as high as 99%.
Now, sampling frames with such high coverages will tend to be relatively representative. Sure, the 1% we're missing may have (very) different characteristics than our entire population. However, any bias caused by their exclusion will be limited because they're so small in number.
The opposite reasoning may or may not hold. That is, a sampling frame with a small coverage
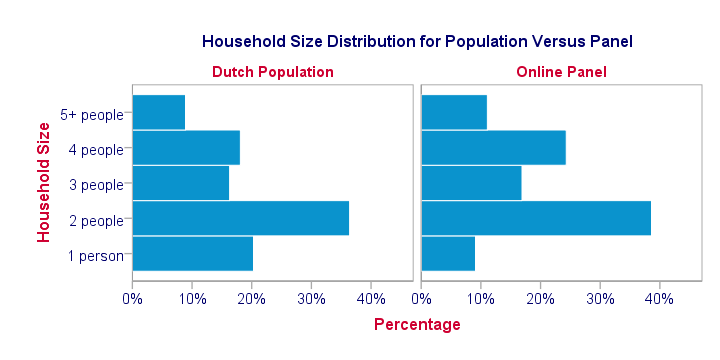
may or may not be representative. For instance, the main panel used by TNS NIPO contains some 213,000 respondents, roughly 1.36% of the Dutch population. However, this sampling frame with a mere 1.36% coverage is remarkably representative for the Dutch population (at least with regard to demographic variables). This is because the demographic makeup of this panel is constantly monitored and panel members are carefully selected from underrepresented groups. The illustration below gives an example.

A remark that's in place here is that a representative sampling frame is not always necessary for drawing a representative sample. In some cases, relevant (demographic) background variables are known for the sampling frame as well as the target population. If so, one can oversample underrepresented groups and undersample overrepresented groups, resulting in a representative gross sample. This procedure is very similar to weighting. But let's first take a look at the gross sample.

Survey Sampling - The Gross Sample

A gross sample is the collection of units that are sampled, regardless whether (usable) data is obtained from them. With regard to surveying people, a gross sample is the group of people who are asked to participate in a survey. In some cases (especially online questionnaires) the gross sample may correspond to the sampling frame; we can simply send out our survey to everyone whose contact details we have.
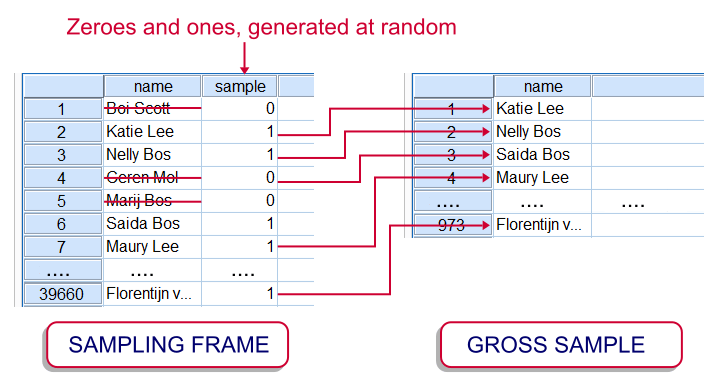
However, some surveys still use face-to-face or phone interviews or paper questionnaires. In case of a huge sampling frame, approaching it entirely may be costly. This is one major reason for sampling from the sampling frame. In practice, the gross sample is often a simple random sample (without replacement) from the sampling frame. The illustration shows how it's typically done in SPSS.

Regarding online panel research, questionnaires are rarely sent out to the entire panel because we don't want to bother the panel members with too many questionnaires. On top of limiting such “respondent burden”, panel members often receive (monetary) incentives for answering questionnaires. This renders it costly to approach an entire (online) panel for a survey.

Survey Sampling - The Nett Sample

A nett sample is the collection of units
from which useful data are obtained. Other than physical objects or animals, people often decline when we try to collect data on them. This phenomenon is aptly named non response. The percentage of a gross sample who do participate in a survey is known as the response rate.
For many studies, response rates typically hover around 20%. This can often be raised by offering incentives or sending out reminders. However, even panel members who clearly stated they're willing to participate in surveys rarely show response rates over some 70%.
After collecting data from the participants, it often turns out that some of them gave nonsensical answers or skipped many questions. We typically remove such respondents altogether from our data. The respondents who do provide us with useful data constitute the nett sample.

Survey Sampling - Selective Non Response

Selective non response is non response that's associated with one or more variables that are relevant for the study. Example: we conduct a customer satisfaction study. In reality, 50% of our customers are satisfied and another 50% are dissatisfied. The same percentages are present in our gross sample. Now, our satisfied customers are willing to help out, resulting in a 70% response rate. Less happy customers may be unwilling to to participate, resulting in a 10% response rate.
In other words: the response rate is associated with customer satisfaction -the single most relevant variable in the entire study. This selective non response results in a nett sample containing 85% satisfied customers. The situation is illustrated by the figure below.

Survey Sampling - Weighting

Weighting is having single observations “count as”
more or less than single observations. For example, a (nett) sample consists of 30 females and 10 males. In this case, we may want to weight this sample: we'll have each female respondent count as only 0.67 respondents and each male respondent as 2 respondents. The figure below shows what this looks like in our data.

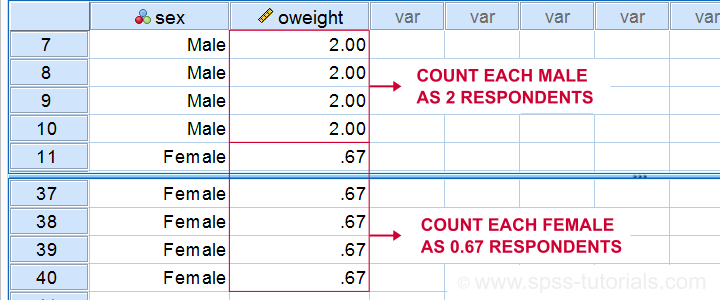A weighted nett sample. Note that the weights are just a variable in our data.

Now 30 females will count as (30 * 0.67 =) 20 respondents and 10 men count as (10 * 2 =) 20 respondents. The weighted sample now consists of 20 males and 20 females.
What the previous example illustrated is that selective non response biases research outcomes. It does so by affecting the representativity of the nett sample.
So how can we prevent bias from selective non response? The most common “fix” to selective non response is weighting the nett sample. A detailed explanation of weighting is beyond the scope of this tutorial.However, see SPSS WEIGHT Command Very briefly, weighting means that underrepresented groups are given more weight in the sample and vice versa for overrepresented groups. The result is a weighted nett sample that may be more representative than its unweighted counterpart.
Importantly, weighting requires that population distributions on relevant background variables are known (or can be reasonably estimated) for the target population. In practice, such frequency distributions are often available only for very general populations (such as all Dutch citizens) on main demographic variables (age, gender). Unfortunately, this information is often insufficient in order to properly weight a sample.
Finally, keep in mind here that weighting violates simple random sampling and therefore biases inferential statistics (such as p-values and confidence intervals) unless special corrections are used.