Most data analysts are familiar with post hoc tests for ANOVA. Oddly, post hoc tests for the chi-square independence test are not widely used. This tutorial walks you through 2 options for obtaining and interpreting them in SPSS.
- Option 1 - CROSSTABS
- CROSSTABS with Pairwise Z-Tests Output
- Option 2 - Custom Tables
- Custom Tables with Pairwise Z-Tests Output
- Can these Z-Tests be Replicated?
Example Data
A sample of N = 300 respondents were asked about their education level and marital status. The data thus obtained are in edu-marit.sav. All examples in this tutorial use this data file.
Chi-Square Independence Test
Right. So let's see if education level and marital status are associated in the first place: we'll run a chi-square independence test with the syntax below. This also creates a contingency table showing both frequencies and column percentages.
crosstabs marit by educ
/cells count column
/statistics chisq.
Let's first take a look at the actual test results shown below.
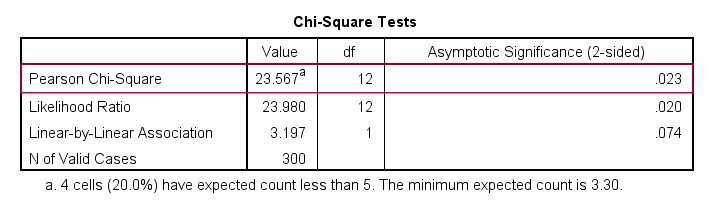
First off, we reject the null hypothesis of independence: education level and marital status are associated, χ2(12) = 23.57, p = 0.023. Note that that SPSS wrongfully reports this 1-tailed significance as a 2-tailed significance. But anyway, what we really want to know is precisely which percentages differ significantly from each other?
Option 1 - CROSSTABS
We'll answer this question by slightly modifying our syntax: adding BPROP (short for “Bonferroni proportions”) to the /CELLS subcommand does the trick.
crosstabs marit by educ
/cells count column bprop. /*bprop = Bonferroni adjusted z-tests for column proportions.
Running this simple syntax results in the table shown below.
CROSSTABS with Pairwise Z-Tests Output
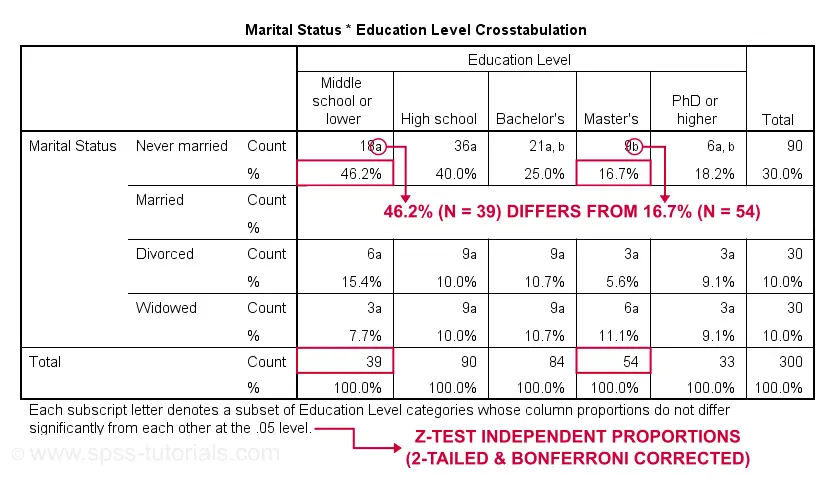
First off, take a close look at the table footnote: “Each subscript letter denotes a subset of Education Level categories whose column proportions do not differ significantly from each other at the .05 level.”
These conclusions are based on z-tests for independent proportions. These also apply to the percentages shown in the table: within each row, each possible pair of percentages is compared using a z-test. If they don't differ, they get a similar subscript. Reversely,
within each row, percentages that don't share a subscript
are significantly different.
For example, the percentage of people with middle school who never married is 46.2% and its frequency of n = 18 is labeled “a”. For those with a Master’s degree, 16.7% never married and its frequency of 9 is not labeled “a”. This means that 46.2% differs significantly from 16.7%.
The frequency of people with a Bachelor’s degree who never married (n = 21 or 25.0%) is labeled both “a” and “b”. It doesn't differ significantly from any cells labeled “a”, “b” or both. Which are all cells in this table row.
Now, a Bonferroni correction is applied for the number of tests within each row. This means that for \(k\) columns,
$$P_{bonf} = P\cdot\frac{k(k - 1)}{2}$$
where
- \(P_{bonf}\) denotes a Bonferroni corrected p-value and
- \(P\) denotes a “normal” (uncorrected) p-value.
Right, now our table has 5 education levels as columns so
$$P_{bonf} = P\cdot\frac{5(5 - 1)}{2} = P \cdot 10$$
which means that each p-value is multiplied by 10 and only then compared to alpha = 0.05. Or -reversely- only z-tests yielding an uncorrected p < 0.005 are labeled “significant”. This holds for all tests reported in this table. I'll verify these claims later on.
Option 2 - Custom Tables
A second option for obtaining “post hoc tests” for chi-square tests are Custom Tables. They're found under

 but only if you have a Custom Tables license. The figure below suggests some basic steps.
but only if you have a Custom Tables license. The figure below suggests some basic steps.
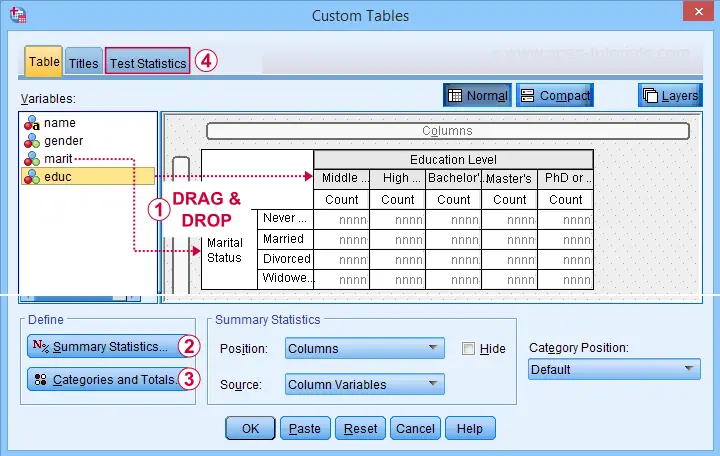
 You probably want to select both frequencies and column percentages for education level.
You probably want to select both frequencies and column percentages for education level.
 We recommend you add totals for education levels as well.
We recommend you add totals for education levels as well.
Next, our z-tests are found in the Test Statistics tab shown below.
Completing these steps results in the syntax below.
CTABLES
/VLABELS VARIABLES=marit educ DISPLAY=DEFAULT
/TABLE marit BY educ [COUNT 'N' F40.0, COLPCT.COUNT '%' PCT40.1]
/CATEGORIES VARIABLES=marit ORDER=A KEY=VALUE EMPTY=INCLUDE TOTAL=YES POSITION=AFTER
/CATEGORIES VARIABLES=educ ORDER=A KEY=VALUE EMPTY=INCLUDE
/CRITERIA CILEVEL=95
/COMPARETEST TYPE=PROP ALPHA=0.05 ADJUST=BONFERRONI ORIGIN=COLUMN INCLUDEMRSETS=YES
CATEGORIES=ALLVISIBLE MERGE=YES STYLE=SIMPLE SHOWSIG=NO.
Custom Tables with Pairwise Z-Tests Output
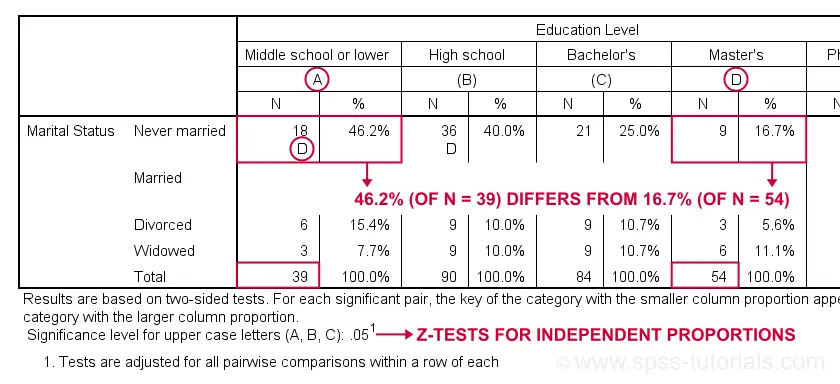
Let's first try and understand what the footnote says: “Results are based on two-sided tests. For each significant pair, the key of the category with the smaller column proportion appears in the category with the larger column proportion. Significance level for upper case letters (A, B, C): .05. Tests are adjusted for all pairwise comparisons within a row of each innermost subtable using the Bonferroni correction.”
Now, for normal 2-way contingency tables, the “innermost subtable” is simply the entire table. Within each row, each possible pair of column proportions is compared using a z-test. If 2 proportions differ significantly, then the higher is flagged with the column letter of the lower. Somewhat confusingly, SPSS flags the frequencies instead of the percentages.
In the first row (never married),
the D in column A indicates that these 2 percentages
differ significantly:
the percentage of people who never married is significantly higher for those who only completed middle school (46.2% from n = 39) than for those who completed a Master’s degree (16.7% from n = 54).
Again, all z-tests use α = 0.05 after Bonferroni correcting their p-values for the number of columns in the table. For our example table with 5 columns, each p-value is multiplied by \(0.5\cdot5(5 - 1) = 10\) before evaluating if it's smaller than the chosen alpha level of 0.05.
Can these Z-Tests be Replicated?
Yes. They can.
Custom Tables has an option to create a table containing the exact p-values for all pairwise z-tests. It's found in the Test Statistics tab. Selecting it results in the syntax below.
CTABLES
/VLABELS VARIABLES=marit educ DISPLAY=DEFAULT
/TABLE marit BY educ [COUNT 'N' F40.0, COLPCT.COUNT '%' PCT40.1]
/CATEGORIES VARIABLES=marit ORDER=A KEY=VALUE EMPTY=INCLUDE TOTAL=YES POSITION=AFTER
/CATEGORIES VARIABLES=educ ORDER=A KEY=VALUE EMPTY=INCLUDE
/CRITERIA CILEVEL=95
/COMPARETEST TYPE=PROP ALPHA=0.05 ADJUST=BONFERRONI ORIGIN=COLUMN INCLUDEMRSETS=YES
CATEGORIES=ALLVISIBLE MERGE=NO STYLE=SIMPLE SHOWSIG=YES.
Exact P-Values for Z-Tests
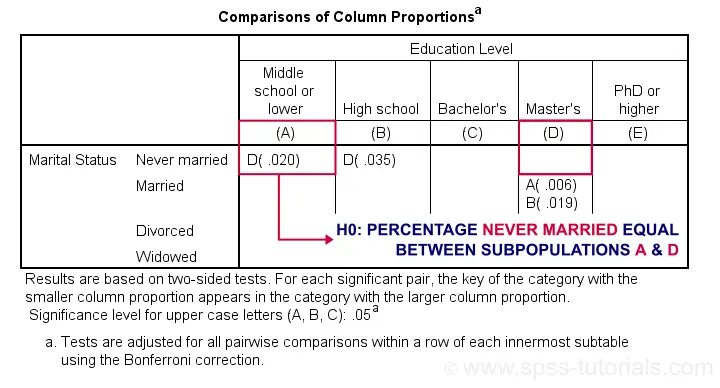
For the first row (never married), SPSS claims that the Bonferroni corrected p-value for comparing column percentages A and D is p = 0.020. For our example table, this implies an uncorrected p-value of p = 0.0020.
We replicated this result with an Excel z-test calculator. Taking the Bonferroni correction into account, it comes up with the exact same p-value as SPSS.
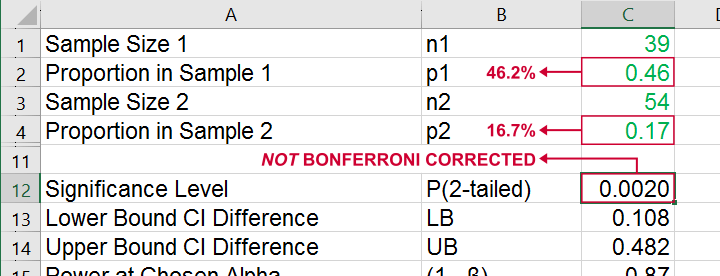
All other p-values reported by SPSS were also exactly replicated by our Excel calculator.
I hope this tutorial has been helpful for obtaining and understanding pairwise z-tests for contingency tables. If you've any questions or feedback, please throw us a comment below.
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 32 COMMENTS:
By Yacoub Hari on October 28th, 2020
Excellent work! Thanks for explaining this!
By Jon Peck on October 28th, 2020
The chi-squared test is generally considered to be a two-tailed test. see
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwiIr7LEoNjsAhWdB50JHSpuCD4QFjASegQIJBAC&url=https%3A%2F%2Fwww.ibm.com%2Fsupport%2Fpages%2Fwhy-does-spss-crosstabs-call-chi-square-tests-2-sided&usg=AOvVaw1M9HiaSMEJyPj6cPsKhg0j
Note that besides Bonferroni, CTABLES offers
The Benjamini-Hochberg correction, which controls the familywise error rate and is somewhat less conservative. With either one, the SPSSINC MODIFY TABLES command can highlight significant cells in the table.
By Muhammed Tahir Muhammed on October 29th, 2020
Thanks so much for this great work.
Sir, can I have a copy of this work?
By Ruben Geert van den Berg on October 29th, 2020
Hi Muhammed!
You can print it as a .pdf file from your web browser. We don't write in WORD or something so we really only have this online version...
Thanks!
SPSS tutorials
By Ruben Geert van den Berg on October 29th, 2020
Hi Jon, thanks for your feedback!
However, I think the IBM document presents a poor justification for a poor decision and is not in line with the standard literature.
I'm not aware of any well-established text book that distinguishes "1-sided" from "1-tailed" significance. If they even mention "1-sided significance" at all, they use it as a synonym for "1-tailed".
Also, for a 4 by 5 table, precisely which are the 2 directions in which the data could deviate from the null hypothesis? I think "directions" doesn't even apply here as there's tons of patterns of observed frequencies which would constitute such a deviation.
Personally, I think it would be better to simply report the significance level as "p" here.