Also see Pearson Correlations - Quick Introduction.
SPSS CORRELATIONS creates tables with Pearson correlations and their underlying N’s and p-values. For Spearman rank correlations and Kendall’s tau, use NONPAR-CORR. Both commands can be pasted from

 .
.
This tutorial quickly walks through the main options. We'll use freelancers.sav throughout and we encourage you to download it and follow along with the examples.
User Missing Values
Before running any correlations, we'll first specify all values of one million dollars or more as user missing values for income_2010 through income_2014.Inspecting their histograms (also see FREQUENCIES) shows that this is necessary indeed; some extreme values are present in these variables and failing to detect them will have a huge impact on our correlations. We'll do so by running the following line of syntax: missing values income_2010 to income_2014 (1e6 thru hi). Note that “1e6” is a shorthand for a 1 with 6 zeroes, hence one million.
SPSS CORRELATIONS - Basic Use
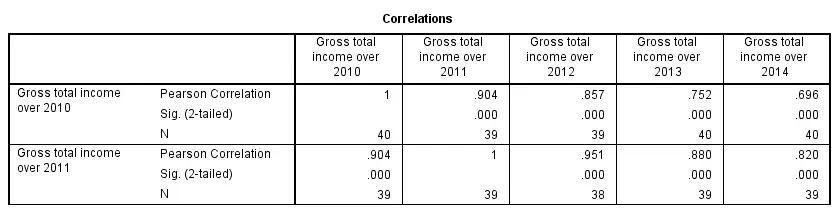
The syntax below shows the simplest way to run a standard correlation matrix. Note that due to the table structure, all correlations between different variables are shown twice.
By default, SPSS uses pairwise deletion of missing values here; each correlation (between two variables) uses all cases having valid values these two variables. This is why N varies from 38 through 40 in the screenshot below.
correlations income_2010 to income_2014.
Keep in mind here that p-values are always shown, regardless of whether their underlying statistical assumptions are met or not. Oddly, SPSS CORRELATIONS doesn't offer any way to suppress them. However, SPSS Correlations in APA Format offers a super easy tool for doing so anyway.
SPSS CORRELATIONS - WITH Keyword
By default, SPSS CORRELATIONS produces full correlation matrices. A little known trick to avoid this is using a WITH clause as demonstrated below. The resulting table is shown in the following screenshot.
correlations income_2010 with income_2011 to income_2014.

SPSS CORRELATIONS - MISSING Subcommand
Instead of the aforementioned pairwise deletion of missing values, listwise deletion is accomplished by specifying it in a MISSING subcommand.An alternative here is identifying cases with missing values by using NMISS. Next, use FILTER to exclude them from the analysis. Listwise deletion doesn't actually delete anything but excludes from analysis all cases having one or more missing values on any of the variables involved.
Keep in mind that listwise deletion may seriously reduce your sample size if many variables and missing values are involved. Note in the next screenshot that the table structure is slightly altered when listwise deletion is used.
correlations income_2010 to income_2014
/missing listwise.

SPSS CORRELATIONS - PRINT Subcommand
By default, SPSS CORRELATIONS shows two-sided p-values. Although frowned upon by many statisticians, one-sided p-values are obtained by specifying ONETAIL on a PRINT subcommand as shown below.
Statistically significant correlations are flagged by specifying NOSIG (no, not SIG) on a PRINT subcommand.
correlations income_2010 with income_2011 to income_2014
/print nosig onetail.
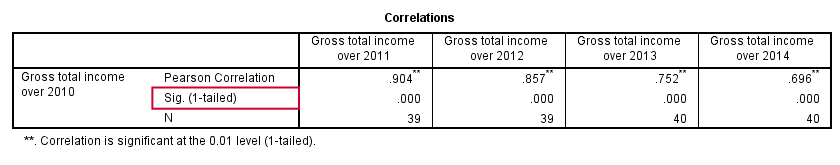
SPSS CORRELATIONS - Notes
More options for SPSS CORRELATIONS are described in the command syntax reference. This tutorial deliberately skipped some of them such as inclusion of user missing values and capturing correlation matrices with the MATRIX subcommand. We did so due to doubts regarding their usefulness.
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 7 COMMENTS:
By Antonije on January 30th, 2017
A nead complitly excercise for scatter matrix
Thenks
Antonije Đukić
By lateef on March 5th, 2017
thanks for the tutorial, but i will like to know your conclusion on the output.
1)I am confuse how you conclude when the sig. is .000
2) what is the null hypothesis that we are rejecting
thanks.
By Ruben Geert van den Berg on March 6th, 2017
Hi Lateef!
The null hypothesis is that the population (Pearson) correlation is precisely zero.
If this is true, we may find a non zero correlation in our sample but it'll probably be close to zero. Sig. (same a "p-value" or just "p") is the probability of finding some correlation in a sample when it is zero in the population. So p is smaller is the correlation differs more from zero. Right? If p = 0.000, it means we've a close to zero probability of finding our sample correlation if the population correlation is zero. So we conclude that the latter probably is not zero after all.
Hope that helps!
By saba on November 7th, 2018
Thank you Ruben for providing such a wonderful guide.
I have one question concerning one-sided p-values in SPSS.
As you know, there are two types of one-sided statistical hypothesis. i. H_0: ϱ = 0 v.s. H_1: ϱ > 0 and ii. H_0: ϱ = 0 v.s. H_1:ϱ < 0. So, SPSS provides one-sided p-value for which type of statistical hypothesis? Thanks
By Ruben Geert van den Berg on November 7th, 2018
Hi Saba!
It depends on the sign of the sample correlation: if r < 0, SPSS tests for ϱ < 0. If r > 0, SPSS tests for ϱ > 0.
But I think you should use 2-tailed p-values whenever possible as I argued in Statistical Significance - What Does It Really Mean?