Contents

• Example Data File
• Prerequisites and Installation
• Example I - Create All Unique Scatterplots
• Example II - Linearity Checks for Predictors

Visualizing your data is the single best thing you can do with it. Doing so may take little effort: a single line FREQUENCIES command in SPSS can create many histograms or bar charts in one go.

Sadly, the situation for scatterplots is different: each of them requires a separate command. We therefore built a tool for creating one, many or all scatterplots among a set of variables, optionally with (non)linear fit lines and regression tables.

Example Data File

We'll use health-costs.sav (partly shown below) throughout this tutorial.

We encourage you to download and open this file and replicate the examples we'll present in a minute.

Prerequisites and Installation

Our tool requires SPSS version 24 or higher. Also, the SPSS Python 3 essentials must be installed (usually the case with recent SPSS versions).

Clicking SPSS_TUTORIALS_SCATTERS.spe downloads our scatterplots tool. You can install it through Extensions Install local extension bundle as shown below.

In the dialog that opens, navigate to the downloaded .spe file and install it. SPSS will then confirm that the extension was successfully installed under Graphs SPSS tutorials - Create All Scatterplots

Example I - Create All Unique Scatterplots

Let's now inspect all unique scatterplots among health costs, alcohol and cigarette consumption and exercise. We'll navigate to Graphs SPSS tutorials - Create All Scatterplots and fill out the dialog as shown below.

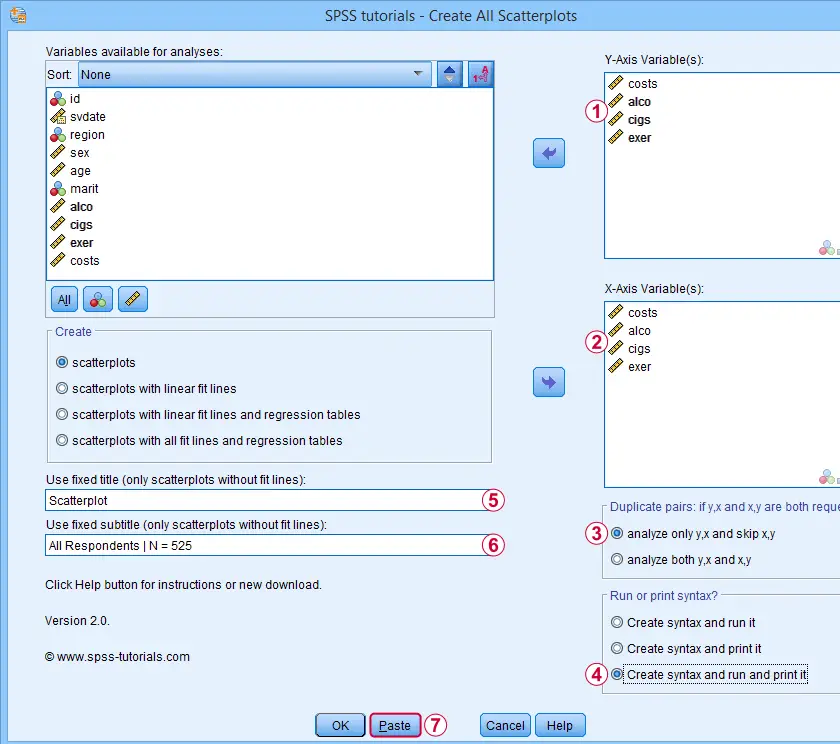
We enter all relevant variables as y-axis variables. We recommend you always first enter the dependent variable (if any).

We enter these same variables as x-axis variables.

This combination of y-axis and x-axis variables results in duplicate chart. For instance, costs by alco is similar alco by costs transposed. Such duplicates are skipped if “analyze only y,x and skip x,y” is selected.

Besides creating scatterplots, we'll also take a quick look at the SPSS syntax that's generated.

If no title is entered, our tool applies automatic titles. For this example, the automatic titles were rather lengthy. We therefore override them with a fixed title (“Scatterplot”) for all charts. The only way to have no titles at all is suppressing them with a chart template.

Clicking Paste results in the syntax below. Let's run it.

SPSS Scatterplots Tool - Syntax I

Results

First off, note that the GRAPH commands that were run by our tool have also been printed in the output window (shown below). You could copy, paste, edit and run these on any SPSS installation, even if it doesn't have our tool installed.

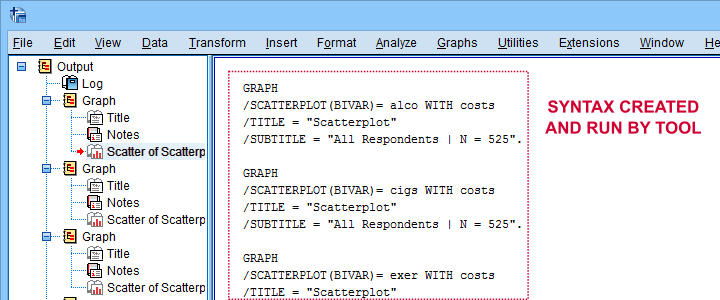
Beneath this syntax, we find all 6 unique scatterplots. Most of them show substantive correlations and all of them look plausible. However, do note that some plots -especially the first one- hint at some curvilinearity. We'll thoroughly investigate this in our second example.

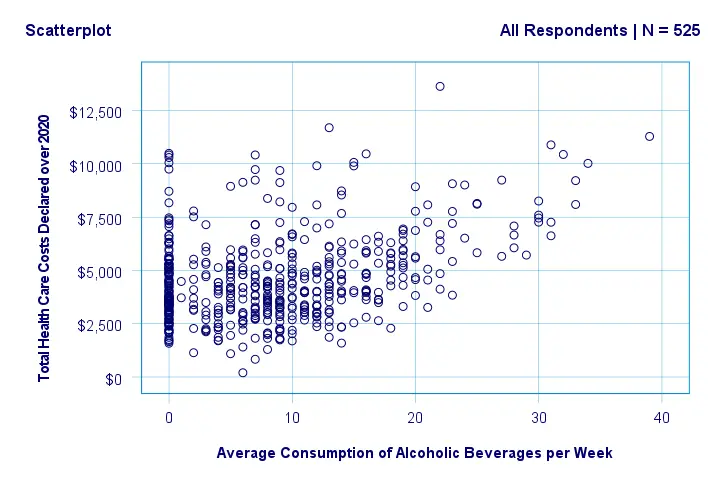
In any case, we feel that a quick look at such scatterplots should always precede an SPSS correlation analysis.

Example II - Linearity Checks for Predictors

I'd now like to run a multiple regression analysis for predicting health costs from several predictors. But before doing so, let's see if each predictor relates linearly to our dependent variable. Again, we navigate to Graphs SPSS tutorials - Create All Scatterplots and fill out the dialog as shown below.

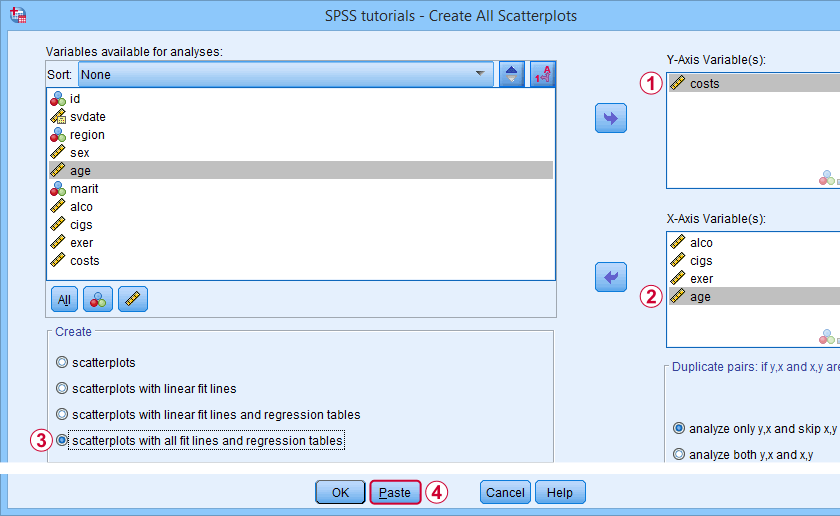
Our dependent variable is our y-axis variable.

All independent variables are x-axis variables.

We'll create scatterplots with all fit lines and regression tables.

We'll run the syntax below after clicking the Paste button.

SPSS Scatterplots Tool - Syntax II

Note that running this syntax triggers some warnings about zero values in some variables. These can safely be ignored for these examples.

Results

In our first scatterplot with regression lines, some curves deviate substantially from linearity as shown below.

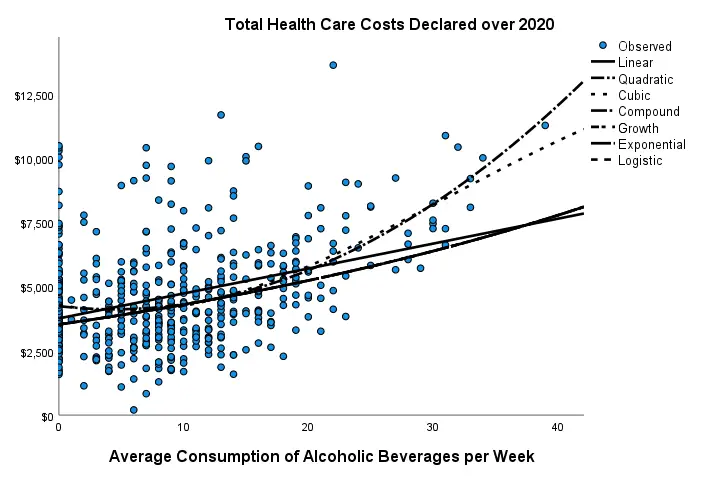
Sadly, this chart's legend doesn't quite help to identify which curve visualizes which transformation function. So let's look at the regression table shown below.

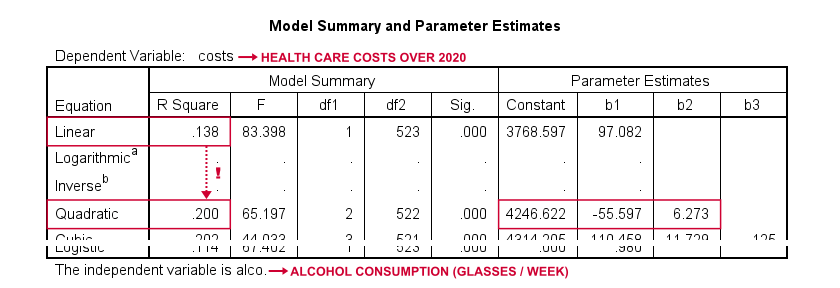
Very interestingly, r-square skyrockets from 0.138 to 0.200 when we add the squared predictor to our model. The b-coefficients tell us that the regression equation for this model is Costs’ = 4,246.22 - 55.597 * alco + 6.273 * alco² Unfortunately, this table doesn't include significance levels or confidence intervals for these b-coefficients. However, these are easily obtained from a regression analysis after adding the squared predictor to our data. The syntax below does just that.

Result

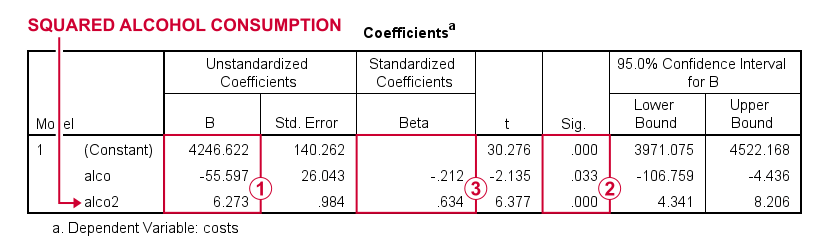
First note that we replicated the exact b-coefficients we saw earlier.

Surprisingly, our squared predictor is more statistically significant than its original, non squared counterpart.

The beta coefficients suggest that the relative strength of the squared predictor is roughly 3 times that of the original predictor.

In short, these results suggest substantial non linearity for at least one predictor. Interestingly, this is not detected by using the standard linearity check: inspecting a scatterplot of standardized residuals versus predicted values after running multiple regression.

But anyway, I just wanted to share the tool I built for these analyses and illustrate it with some typical examples. Hope you found it helpful!

If you've any feedback, we always appreciate if you throw us a comment below.

Thanks for reading!