• Method A - Legacy Dialogs
• Method B - Chart Builder
• Method C - CURVEFIT
• Method D - Regression Variable Plots
• Method E - All Scatterplots Tool

Summary & Example Data

This tutorial walks you through different options for drawing (non)linear regression lines for either all cases or subgroups. All examples use bank-clean.sav, partly shown below.

Method A - Legacy Dialogs

A simple option for drawing linear regression lines is found under Graphs Legacy Dialogs Scatter/Dot as illustrated by the screenshots below.

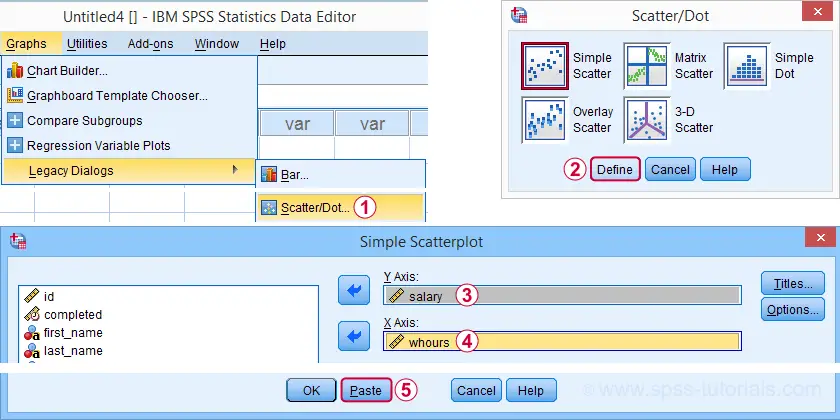
Completing these steps results in the SPSS syntax below. Running it creates a scatterplot to which we can easily add our regression line in the next step.

For adding a regression line, first double click the chart to open it in a Chart Editor window. Next, click the “Add Fit Line at Total” icon as shown below.

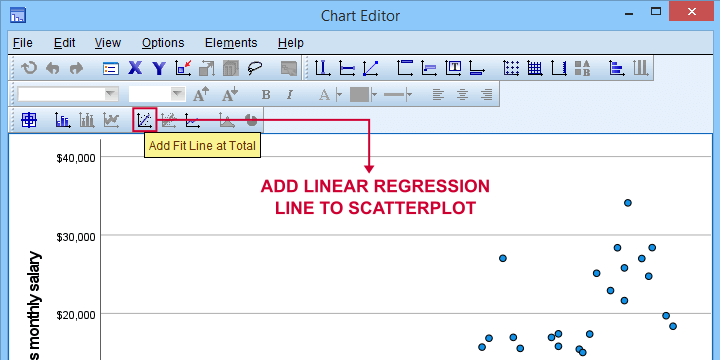
You can now simply close the fit line dialog and Chart Editor.

Result

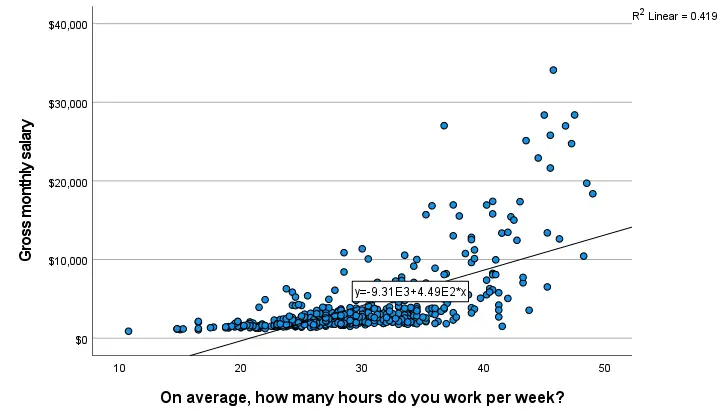
The linear regression equation is shown in the label on our line: y = 9.31E3 + 4.49E2*x which means that

$$Salary' = 9,310 + 449 \cdot Hours$$

Note that 9.31E3 is scientific notation for 9.31 · 10³ = 9,310 (with some rounding).

You can verify this result and obtain more detailed output by running a simple linear regression from the syntax below.

When doing so, you'll also have significance levels and/or confidence intervals. Finally, note that a linear relation seems a very poor fit for these variables. So let's explore some more interesting options.

Method B - Chart Builder

For SPSS versions 25 and higher, you can obtain scatterplots with fit lines from the chart builder. Let's do so for job type groups separately: simply navigate to Graphs Chart Builder and fill out the dialogs as shown below.

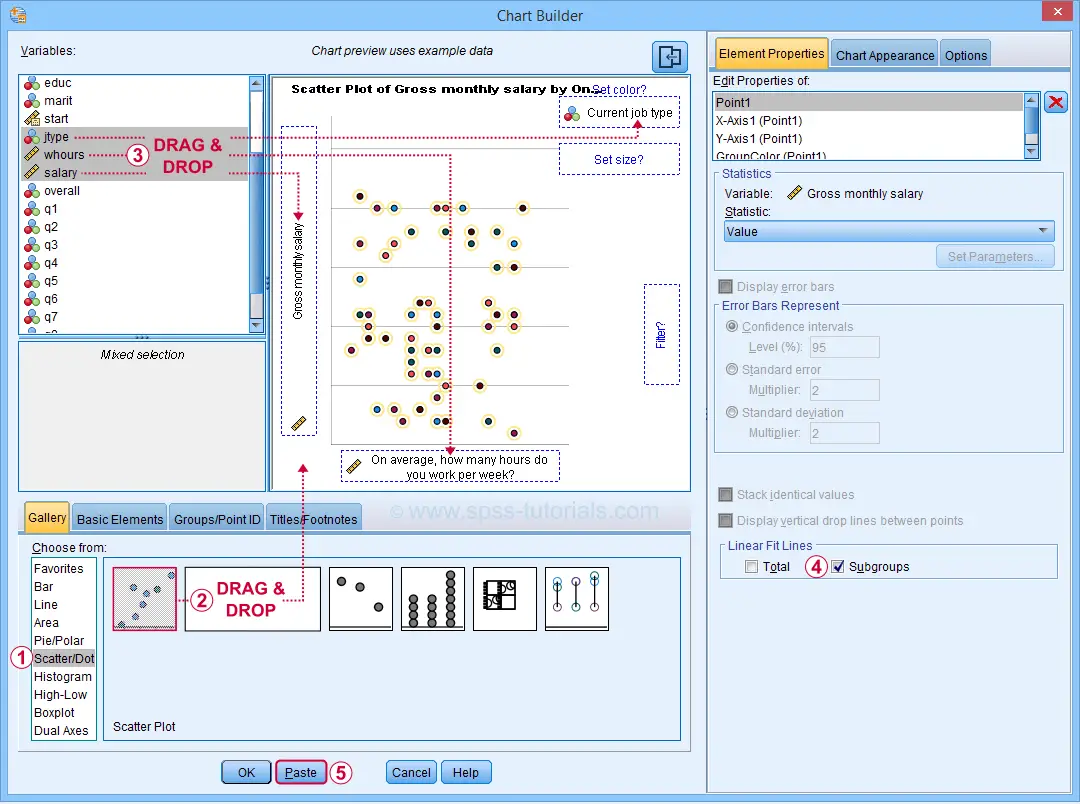
This results in the syntax below. Let's run it.

Result

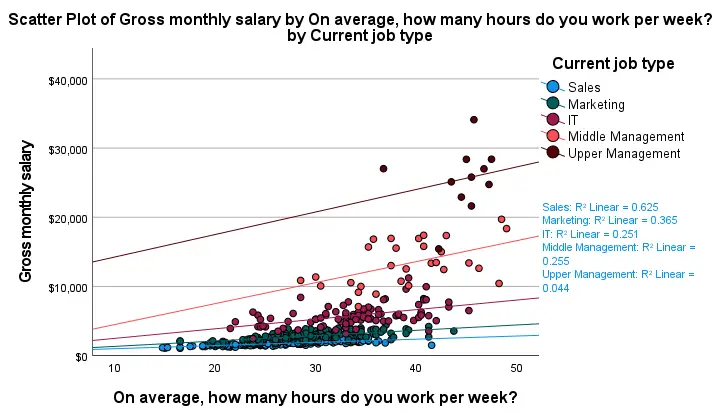
First off, this chart is mostly used for

• inspecting homogeneity of regression slopes in ANCOVA and
• simple slopes analysis in moderation regression.

Sadly, the styling for this chart is awful but we could have fixed this with a chart template if we hadn't been so damn lazy.

Anyway, note that R-square -a common effect size measure for regression- is between good and excellent for all groups except upper management. This handful of cases may be the main reason for the curvilinearity we see if we ignore the existence of subgroups.

Running the syntax below verifies the results shown in this plot and results in more detailed output.

Method C - CURVEFIT

Scatterplots with (non)linear fit lines and basic regression tables are very easily obtained from CURVEFIT. Jus navigate to Analyze Regression Curve Estimation and fill out the dialog as shown below.

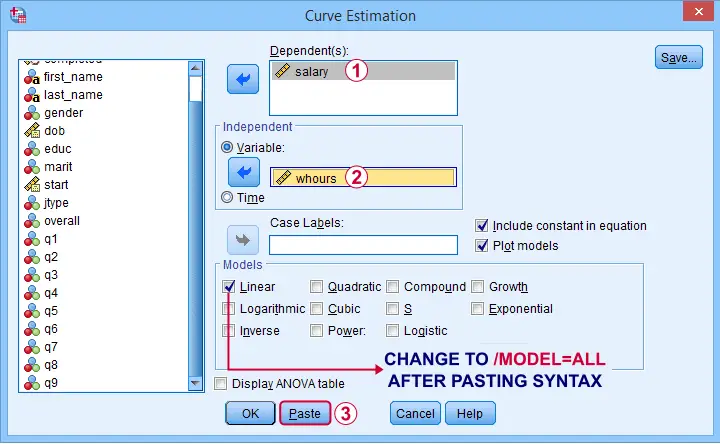
If you'd like to see all models, change /MODEL=LINEAR to /MODEL=ALL after pasting the syntax.

Result

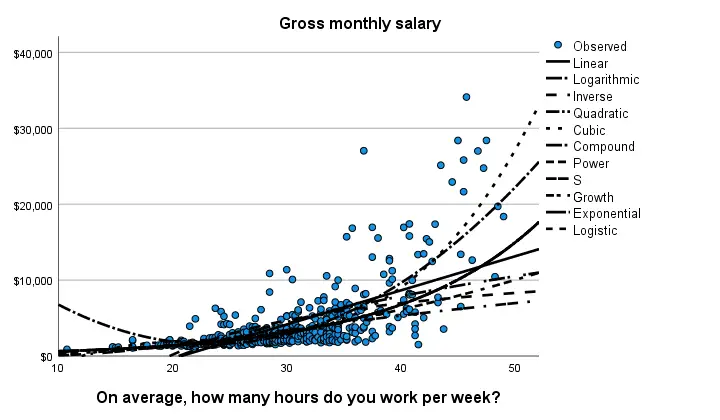
Despite the poor styling of this chart, most curves seem to fit these data better than a linear relation. This can somewhat be verified from the basic regression table shown below.

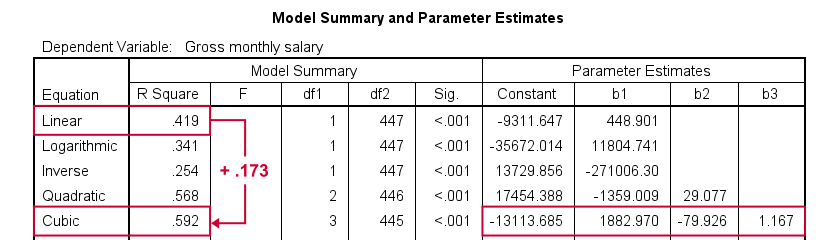
Especially the cubic model seems to fit nicely. Its equation is

$$Salary' = -13114 + 1883 \cdot hours - 80 \cdot hours^2 + 1.17 \cdot hours^3$$

Sadly, this output is rather limited: do all predictors in the cubic model seriously contribute to r-squared? The syntax below results in more detailed output and verifies our initial results.

Method D - Regression Variable Plots

Regression Variable Plots is an SPSS extension that's mostly useful for

• creating several scatterplots and/or fit lines in one go;
• plotting nonlinear fit lines for separate groups;
• adding elements to and customizing these charts.

I believe this extension is preinstalled with SPSS version 26 onwards. If not, it's supposedly available from STATS_REGRESS_PLOT but I used to have some trouble installing it on older SPSS versions.

Anyway: if installed, navigating to Graphs Regression Variable Plots should open the dialog shown below.

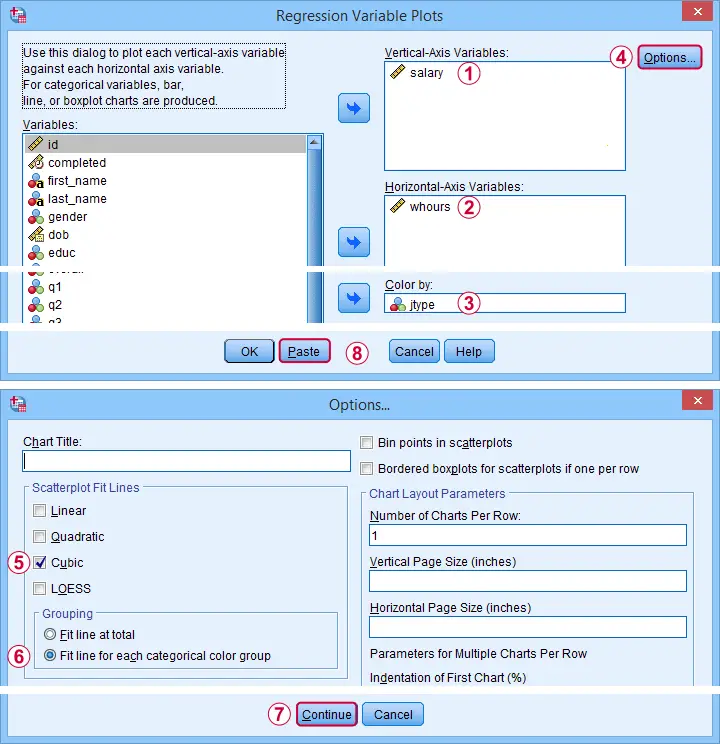
Completing these steps results in the syntax below. Let's run it.

Result

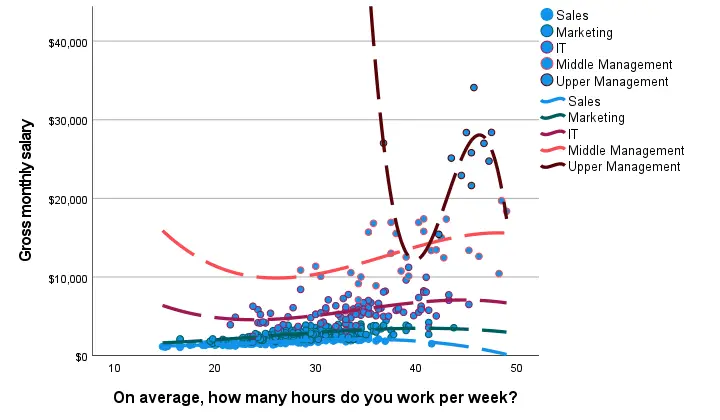
Most groups don't show strong deviations from linearity. The main exception is upper management which shows a rather bizarre curve.

However, keep in mind that these are only a handful of observations; the curve is the result of overfitting. It (probably) won't replicate in other samples and can't be taken seriously.

Method E - All Scatterplots Tool

Most methods we discussed so far are pretty good for creating a single scatterplot with a fit line. However, we often want to check several such plots for things like outliers, homoscedasticity and linearity. This is especially relevant for

• multiple regression analysis and
• correlation analysis.

A very simple tool for precisely these purposes is downloadable from and discussed in SPSS - Create All Scatterplots Tool.

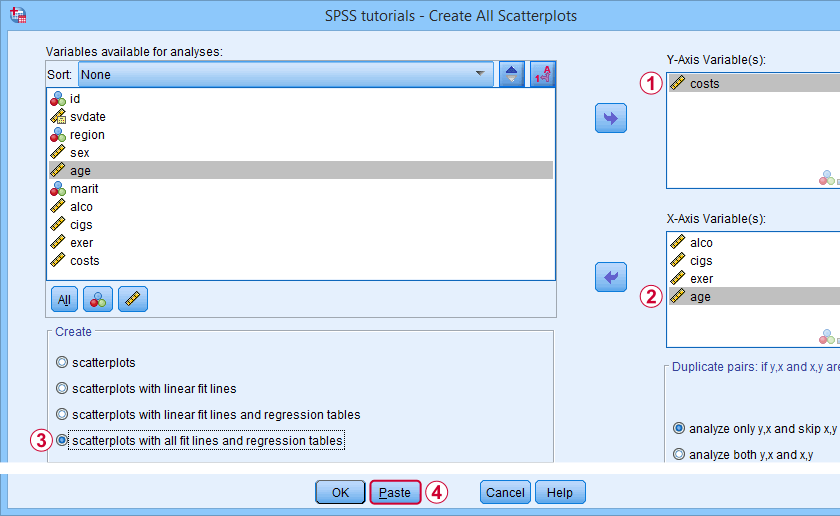
Final Notes

Right, so those are the main options for obtaining scatterplots with fit lines in SPSS. I hope you enjoyed this quick tutorial as much as I have.

If you've any remarks, please throw me a comment below. And last but not least:

thanks for reading!