Kendall’s Concordance Coefficient W is a number between 0 and 1
that indicates interrater agreement.
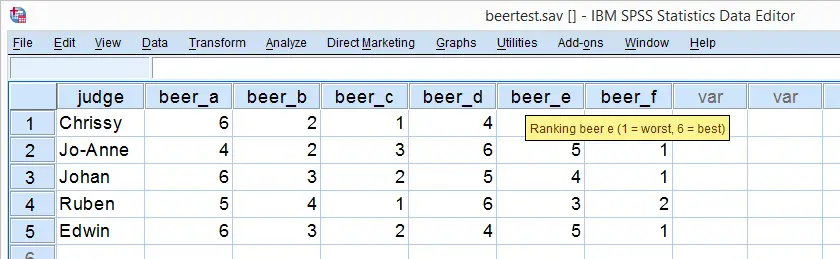
So let's say we had 5 people rank 6 different beers as shown below. We obviously want to know which beer is best, right? But could we also quantify how much these raters agree with each other? Kendall’s W does just that.
Kendall’s W - Example
So let's take a really good look at our beer test results. The data -shown above- are in beertest.sav. For answering which beer was rated best, a Friedman test would be appropriate because our rankings are ordinal variables. A second question, however, is to what extent do all 5 judges agree on their beer rankings? If our judges don't agree at all which beers were best, then we can't possibly take their conclusions very seriously. Now, we could say that “our judges agreed to a large extent” but we'd like to be more precise and express the level of agreement in a single number. This number is known as Kendall’s Coefficient of Concordance W.2,3
Kendall’s W - Basic Idea
Let's consider the 2 hypothetical situations depicted below: perfect agreement and perfect disagreement among our raters. I invite you to stare at it and think for a minute.
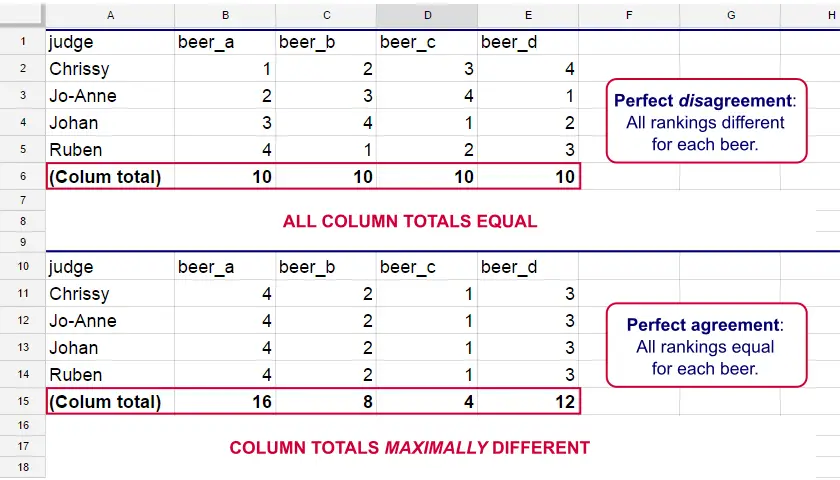
As we see, the extent to which raters agree is indicated by the extent to which the column totals differ. We can express the extent to which numbers differ as a number: the variance or standard deviation.
Kendall’s W is defined as
$$W = \frac{Variance\,over\,column\,totals}{Maximum\,possible\,variance\,over\,column\,totals}$$
As a result, Kendall’s W is always between 0 and 1. For instance, our perfect disagreement example has W = 0; because all column totals are equal, their variance is zero.
Our perfect agreement example has W = 1 because the variance among column totals is equal to the maximal possible variance. No matter how you rearrange the rankings, you can't possibly increase this variance any further. Don't believe me? Give it a go then.
So what about our actual beer data? We'll quickly find out with SPSS.
Kendall’s W in SPSS
We'll get Kendall’s W from SPSS’ menu. The screenshots below walk you through.
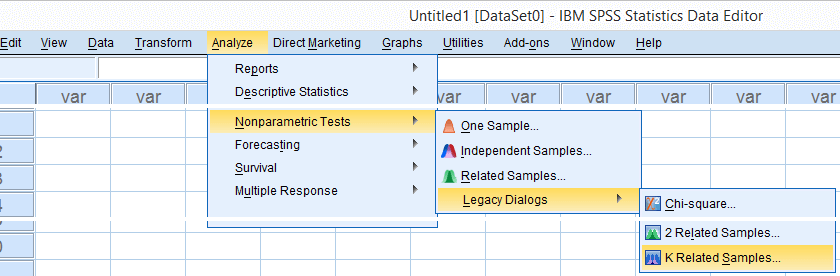
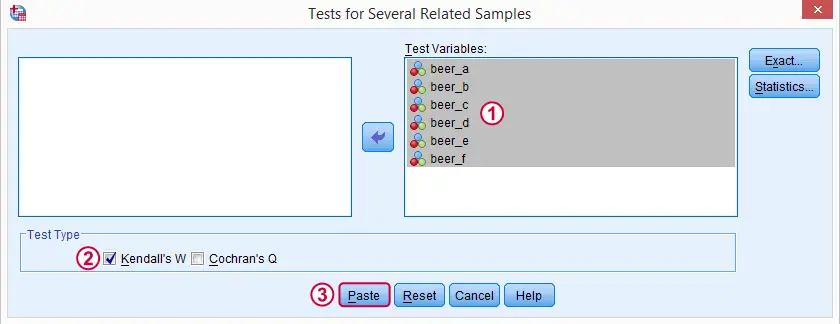
Note: SPSS thinks our rankings are nominal variables. This is because they contain few distinct values. Fortunately, this won't interfere with the current analysis. Completing these steps results in the syntax below.
Kendall’s W - Basic Syntax
NPAR TESTS
/KENDALL=beer_a beer_b beer_c beer_d beer_e beer_f
/MISSING LISTWISE.
Kendall’s W - Output

And there we have it: Kendall’s W = 0.78. Our beer judges agree with each other to a reasonable but not super high extent. Note that we also get a table with the (column) mean ranks that tells us which beer was rated most favorably.
Average Spearman Correlation over Judges
Another measure of concordance is the average over all possible Spearman correlations among all judges.1 It can be calculated from Kendall’s W with the following formula
$$\overline{R}_s = {kW - 1 \over k - 1}$$
where \(\overline{R}_s\) denotes the average Spearman correlation and \(k\) the number of judges.
For our example, this comes down to
$$\overline{R}_s = {5(0.781) - 1 \over 5 - 1} = 0.726$$
We'll verify this by running and averaging all possible Spearman correlations in SPSS. We'll leave that for a next tutorial, however, as doing so properly requires some highly unusual -but interesting- syntax.
Thank you for reading!
References
- Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
- Slotboom, A. (1987). Statistiek in woorden [Statistics in words]. Groningen: Wolters-Noordhoff.
- Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [Statistics, part 3]. Amsterdam: Boom.
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 27 COMMENTS:
By Rev on May 9th, 2023
Thank you for your quick response.
I have another question. While reporting Kendall's W coefficient, do we need to report the p-value as well? What I understand is for intermediate values between 0-1, the interpretation is intermediate agreement, and higher the W
By Rev on May 9th, 2023
(Some technical glitch happened while posting my question, continuing it here)
So, what I understand is higher the W value greater agreement. So is it like if the p value is significant, its only then we go for the interpretation?