SPSS one-sample chi-square test is used to test whether a single categorical variable follows a hypothesized population distribution.

SPSS One-Sample Chi-Square Test Example

A marketeer believes that 4 smartphone brands are equally attractive. He asks 43 people which brand they prefer, resulting in brands.sav. If the brands are really equally attractive, each brand should be chosen by roughly the same number of respondents. In other words, the expected frequencies under the null hypothesis are (43 cases / 4 brands =) 10.75 cases for each brand. The more the observed frequencies differ from these expected frequencies, the less likely it is that the brands really are equally attractive.

1. Quick Data Check

Before running any statistical tests, we always want to have an idea what our data basically look like. In this case we'll inspect a histogram of the preferred brand by running FREQUENCIES. We'll open the data file and create our histogram by running the syntax below. Since it's very simple, we won't bother about clicking through the menu here.

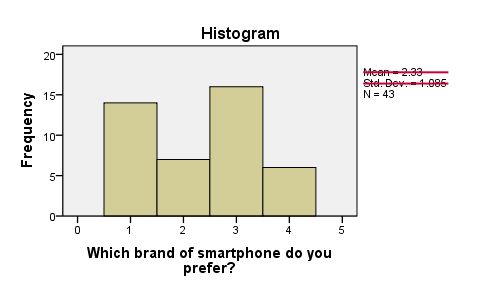
First, N = 43 means that the histogram is based on 43 cases. Since this is our sample size, we conclude that no missing values are present. SPSS also calculates a mean and standard deviation but these are not meaningful for nominal variables so we'll just ignore them. Second, the preferred brands have rather unequal frequencies, casting some doubt upon the null hypothesis of those being equal in the population.

Assumptions One-Sample Chi-Square Test

1. independent and identically distributed variables (or “independent observations”);
2. none of the expected frequencies are < 5;

The first assumption is beyond the scope of this tutorial. We'll presume it's been met by our data. Whether the assumption 2 holds is reported by SPSS whenever we run a one-sample chi-square test. However, we already saw that all expected frequencies are 10.75 for our data.

3. Run SPSS One Sample Chi-Square Test

Expected Values refers to the expected frequencies, the aforementioned 10.75 cases for each brand. We could enter these values but selecting All categories equal is a faster option and yields identical results.
Clicking Paste results in the syntax below.

4. SPSS One-Sample Chi-Square Test Output

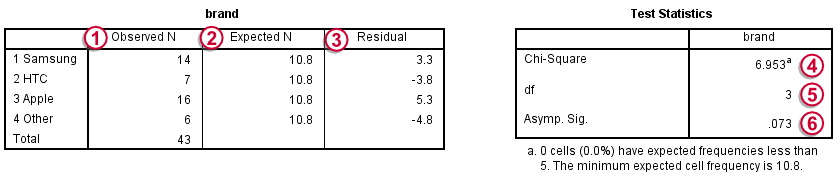
Under Observed N we find the observed frequencies that we saw previously;
under Expected N we find the theoretically expected frequencies;They're shown as 10.8 instead of 10.75 due to rounding. All reported decimals can be seen by double-clicking the value.
for each frequency the Residual is the difference between the observed and the expected frequency and thus expresses a deviation from the null hypothesis;
the Chi-Square test statistic sort of summarizes the residuals and hence indicates the overall difference between the data and the hypothesis. The larger the chi-square value, the less the data “fit” the null hypothesis;
degrees of freedom (df) specifies which chi-square distribution applies;
Asymp. Sig. refers to the p value and is .073 in this case. If the brands are exactly equally attractive in the population, there's a 7.3% chance of finding our observed frequencies or a larger deviation from the null hypothesis. We usually reject the null hypothesis if p < .05. Since this is not the case, we conclude that the brands are equally attractive in the population.

Reporting a One-Sample Chi-Square Test

When reporting a one-sample chi-square test, we always report the observed frequencies. The expected frequencies usually follow readily from the null hypothesis so reporting them is optional. Regarding the significance test, we usually write something like “we could not demonstrate that the four brands are not equally attractive; χ²(3) = 6.95, p = .073.”