Kendall’s Tau is a number between -1 and +1
that indicates to what extent 2 variables are monotonously related.
- Kendall’s Tau - Formulas
- Kendall’s Tau - Exact Significance
- Kendall’s Tau - Confidence Intervals
- Kendall’s Tau versus Spearman Correlation
- Kendall’s Tau - Interpretation
Kendall’s Tau - What is It?
Kendall’s Tau is a correlation suitable for quantitative and ordinal variables. It indicates how strongly 2 variables are monotonously related:
to which extent are high values on variable x are associated with
either high or low values on variable y?
Like so, Kendall’s Tau serves the exact same purpose as the Spearman rank correlation. The reasoning behind the 2 measures, however, is different. Let's take a look at the example data shown below.
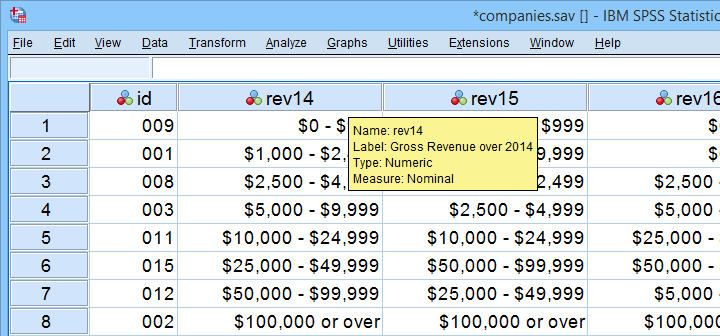
These data show yearly revenues over the years 2014 through 2018 for several companies. We'd like to know to what extent companies that did well in 2014 also did well in 2015. Note that we only have revenue categories and these are ordinal variables: we can rank them but we can't compute means, standard deviations or correlations over them.
Kendall’s Tau - Intersections Method
If we rank both years, we can inspect to what extent these ranks are different. A first step is to connect the 2014 and the 2015 ranks with lines as shown below.
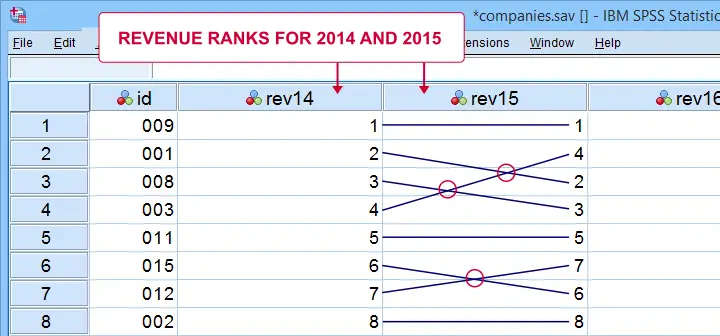
Our connection lines show 3 intersections. These are caused by the 2014 and 2015 rankings being slightly different. Note that the more the ranks differ, the more intersections we see:
- if 2 rankings are identical, we have zero intersections and
- if 2 rankings are exactly opposite, the number of intersections is
$$0.5\cdot n(n - 1)$$
This is the maximum number of intersections for \(n\) observations. Dividing the actual number of intersections by the maximum number of intersections is the basis for Kendall’s tau, denoted by \(\tau\) below.
$$\tau = 1 - \frac{2\cdot I}{0.5\cdot n(n - 1)}$$
where \(I\) is the number of intersections. For our example data with 3 intersections and 8 observations, this results in
$$\tau = 1 - \frac{2\cdot 3}{0.5\cdot 8(8 - 1)} =$$
$$\tau = 1 - \frac{6}{28} \approx 0.786$$
Since \(\tau\) runs from -1 to +1, \(\tau\) = 0.786 indicates a strong positive relation: higher revenue ranks in 2014 are associated with higher ranks in 2015.
Kendall’s Tau - Concordance Method
A second method to find Kendall’s Tau is to inspect all unique pairs of observations. We did so in this Googlesheet shown below.
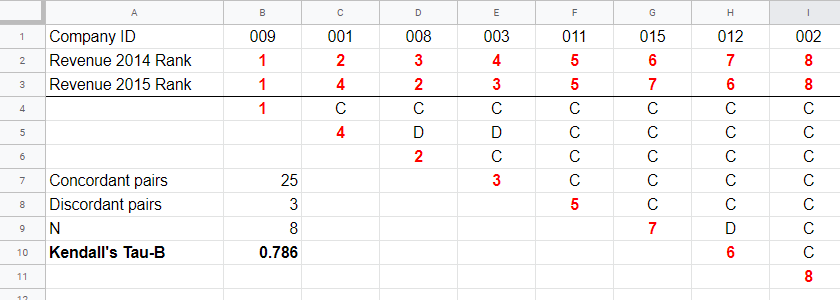
Starting at row 4, each 2015 rank is compared to all 2014 ranks to its right. If these are higher, we have concordant pairs of observations denoted by C. These indicate a positive relation.
However, 2015 ranks having larger 2014 ranks to their right indicate discordant pairs denoted by D. For instance, cell D5 is discordant because the 2014 rank (3) is smaller than the 2015 rank of 4. Discordant pairs indicate a negative relation.
Finally, Kendall’s Tau can be computed from the numbers of concordant and discordant pairs with
$$\tau = \frac{n_c - n_d}{0.5\cdot n(n - 1)}$$
for our example with 3 discordant and 25 concordant pairs in 8 observations, this results in
$$\tau = \frac{25 - 3}{0.5\cdot 8(8 - 1)} = $$
$$\tau = \frac{22}{28} \approx 0.786.$$
Note that C and D add up to the number of unique pairs of observations, \(0.5\cdot n(n - 1)\) which results 28 in our example. Keeping this in mind, you may see that
- \(\tau\) = -1 if all pairs are discordant;
- \(\tau\) = 0 if the numbers of concordant and discordant pairs are equal and
- \(\tau\) = 1 if all pairs are concordant.
Kendall’s Tau-B & Tau-C
Our first method for computing Kendall’s Tau only works if each company falls into a different revenue category. This holds for the 2014 and 2015 data. For 2017 and 2018, however, some companies fall into the same revenue categories. These variables are said to contain ties. Two modified formulas are used for this scenario:
- Kendall’s tau-b corrects for ties and
- Kendall’s tau-c ignores ties.
Simply “Kendall’s Tau” usually refers Kendall’s Tau-b. We won't discuss Kendall’s Tau-c as it's not often used anymore. In the absence of ties, both formulas yield identical results.
Kendall’s Tau - Formulas
So how could we deal with ties? First off, mean ranks are assigned to tied observations as in this Googlesheet shown below: companies 009 and 001 share the two lowest 2016 ranks so they are both ranked the mean of ranks 1 and 2, resulting in 1.5.
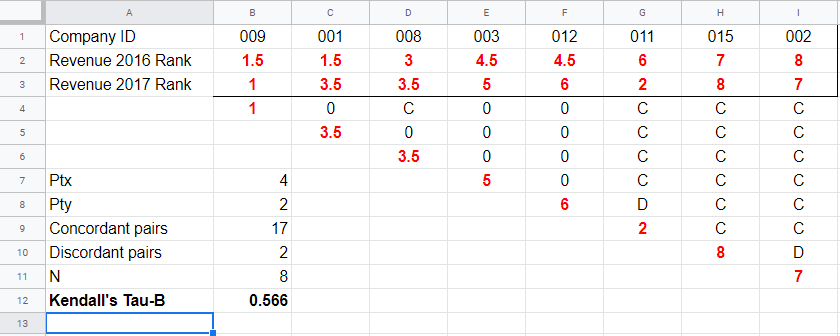
Second, pairs associated with tied 2016 observations are neither concordant nor discordant. Such pairs (columns B,C and E,F) receive a 0 rather than a C or a D. Third, 2017 ranks that have a 2017 tie to their right are also assigned 0. Like so, the 28 pairs in the example above result in
- 17 concordant pairs (C),
- 2 discordant pairs (D) and
- 9 inconclusive pairs (0).
For computing \(\tau_b\), ties on either variable result in a penalty computed as
$$Pt = \Sigma{(t_i^2 - t_i)}$$
where \(t_i\) denotes the length of the \(i\)th tie for either variable. The 2016 ranks have 2 ties -both of length 2- resulting in
$$Pt_{2016} = (2^2 - 2) + (2^2 - 2) = 4$$
Similarly,
$$Pt_{2017} = (2^2 - 2) = 2$$
Finally, \(\tau_b\) is computed with
$$\tau_b = \frac{2\cdot (C - D)}{\sqrt{n(n - 1) - Pt_x}\sqrt{n(n - 1) - Pt_y}}$$
For our example, this results in
$$\tau_b = \frac{2\cdot (17 - 2)}{\sqrt{8(8 - 1) - 4}\sqrt{8(8 - 1) - 2}} =$$
$$\tau_b = \frac{30}{\sqrt{52}\sqrt{54}} \approx 0.566$$
Kendall’s Tau - Exact Significance
For small sample sizes of N ≤ 10, the exact significance level for \(\tau_b\) can be computed with a permutation test. The table below gives critical values for α = 0.05 and α = 0.01.
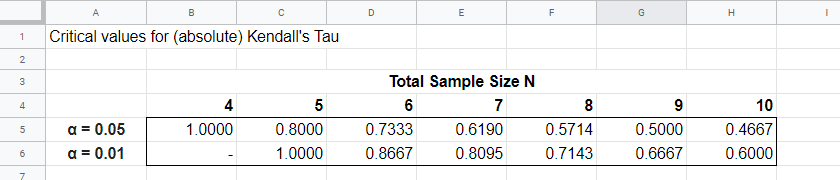
Our example calculation without ties resulted in \(\tau_b\) = 0.786 for 8 observations. Since \(|\tau_b|\) > 0.7143, p < 0.01: we reject the null hypothesis that \(\tau_b\) = 0 in the entire population. Basic conclusion: revenues over 2014 and 2015 are likely to have a positive monotonous relation in the entire population of companies.
The second example (with ties) resulted in \(\tau_b\) = 0.566 for 8 observations. Since \(|\tau_b|\) < 0.5714, p > 0.05. We retain the null hypothesis: our sample outcome is not unlikely if revenues over 2016 and 2017 are not monotonously related in the entire population.
Kendall’s Tau-B - Asymptotic Significance
For sample sizes of N > 10,
$$z = \frac{3\tau_b\sqrt{n(n - 1)}}{\sqrt{2(2n + 5)}}$$
roughly follows a standard normal distribution. For example, if \(\tau_b\) = 0.500 based on N = 12 observations,
$$z = \frac{3\cdot 0.500 \sqrt{12(11)}}{\sqrt{2(24 + 5)}} \approx 2.263$$
We can easily look up that \(p(|z| \gt 2.263) \approx 0.024\): we reject the null hypothesis that \(\tau_b\) = 0 in the population at α = 0.05 but not at α = 0.01.
Kendall’s Tau - Confidence Intervals
Confidence intervals for \(\tau_b\) are easily obtained from JASP. The screenshot below shows an output example.

We presume that these confidence intervals require sample sizes of N > 10 but we couldn't find any reference on this.
Kendall’s Tau versus Spearman Correlation
Kendall’s Tau serves the exact same purpose as the Spearman rank correlation: both indicate to which extent 2 ordinal or quantitative variables are monotonously related. So which is better? Some general guidelines are that
- the statistical properties -sampling distribution and standard error- are better known for Kendall’s Tau than for Spearman-correlations. Kendall’s Tau also converges to a normal distribution faster (that is, for smaller sample sizes). The consequence is that significance levels and confidence intervals for Kendall’s Tau tend to be more reliable than for Spearman correlations.
- absolute values for Kendall’s Tau tend to be smaller than for Spearman correlations: when both are calculated on the same data, we typically see something like \(|\tau_b| \approx 0.7\cdot |R_s|\).
- Kendall’s Tau typically has smaller standard errors than Spearman correlations. Combined with the previous point, the significance levels for Kendall’s Tau tend to be roughly equal to those for Spearman correlations.
In order to illustrate point 2, we computed Kendall’s Tau and Spearman correlations on 8 simulated variables, v1 through v8. The colors shown below are linearly related to the absolute values.
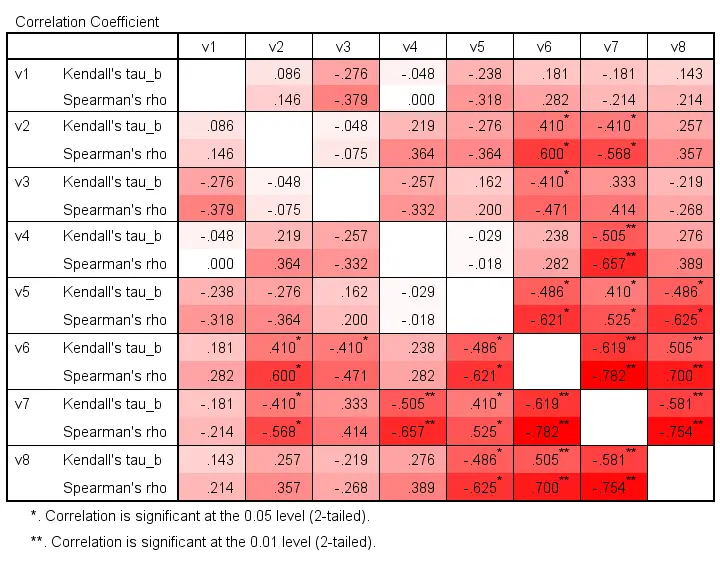
For basically all cells, the second line (Spearman correlation) is darker, indicating a larger absolute value. Also, \(|\tau_b| \approx 0.7\cdot |R_s|\) seems a rough but reasonable rule of thumb for most cells.
The significance levels for the same variables are shown below.
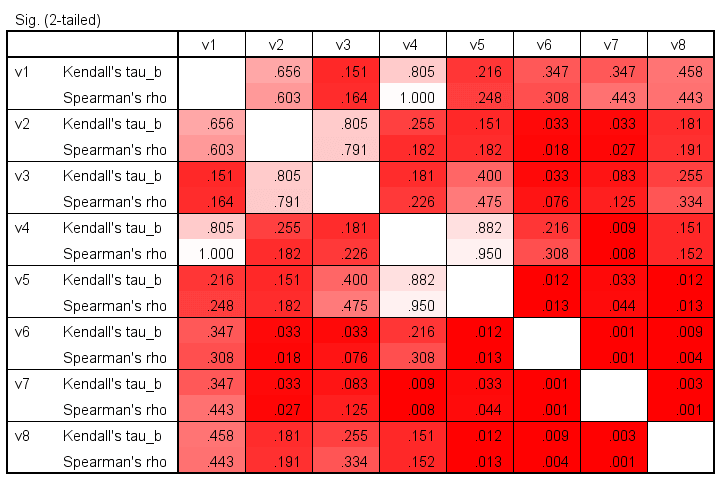
These colors show no clear pattern: sometimes Kendall’s Tau is “more significant” than Spearman’s rho and sometimes the reverse is true. Also note that the significance levels tend to be more similar than the actual correlations. Sadly, the positive skewness of these p-values results in limited dispersion among the colors.
Kendall’s Tau - Interpretation
- \(\tau_b\) = -1 indicates a perfect negative monotonous relation among 2 variables: a lower score on variable A is always associated with a higher score on variable B;
- \(\tau_b\) = 0 indicates no monotonous relation at all;
- \(\tau_b\) = 1 indicates a perfect positive monotonous relation: a lower score on variable A is always associated with a lower score on variable B.
The values of -1 and +1 can only be attained if both variables have equal numbers of distinct ranks, resulting in a square contingency table.
Furthermore, if 2 variables are independent, \(\tau_b\) = 0 but the reverse does not always hold: a curvilinear or other non monotonous relation may still exist.
We didn't find any rules of thumb for interpreting \(\tau_b\) as an effect size so we'll propose some:
- \(|\tau_b|\) = 0.07 indicates a weak association;
- \(|\tau_b|\) = 0.21 indicates a medium association;
- \(|\tau_b|\) = 0.35 indicates a strong association.
Kendall’s Tau-B in SPSS
The simplest option for obtaining Kendall’s Tau from SPSS is from the correlations dialog as shown below.
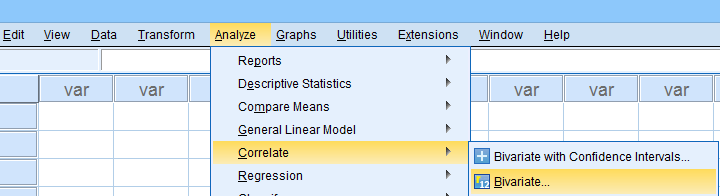
Alternatively (and faster), use simplified syntax such as
nonpar corr rev14 to rev18
/print kendall nosig.
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 17 COMMENTS:
By Jorge Ortiz Pinilla on June 13th, 2020
Hi, I have this question asked by an SPSS user:
"I'm running a correlation analysis between a set of variables in SPSS. In a first analysis, I ran a crosstab analysis entering variables as rows and columns and performed both Spearman, Kendall's Tau-b, and Tau-c correlation tests and annotated the results. In a second moment, I performed the same analysis, but going trough the bivariate correlation option in SPSS to obtain a correlation matrix and to facilitate the view of significant correlations. It turned out that for Kendall's correlation, the p-values were different between analyses, despite the correlation coefficient and the number of valid samples being identical.
E.g.: For a given correlation I've got Tau-b = 0.175; p = 0.032; N = 75 in the first analysis, but obtained Tau-b = 175; p = 0.067; N = 75. For the Spearman's correlation the results were consistent between analyses, Rho = 0.213; p = 0.067; N = 75.
Can somebody grasp why this occurs? There are differences in p-value estimations when running correlation analyses in these two ways or it is probably an error?
in both cases the analyses were two-tailed."
Thank you for your answer
Jorge Ortiz
By Ruben Geert van den Berg on June 17th, 2020
Hi Jorge!
For some statistics, SPSS can compute the exact p-value but this requires a lot of processing time for larger sample sizes.
In order to avoid that, SPSS often computes an approximate p-value (using different formulas). For large sample sizes, the approximate p-values are basically identical to the exact p-values.
However, they may be quite different for small sample sizes. Therefore, SPSS should compute exact p-values here but it doesn't always do so.
Whether an exact or approximate p-value is computed may even depend on which SPSS dialog you use to compute it.
I can confirm that this holds for the Kolmogorov-Smirnov test as well as Spearman rank correlations. I think it also goes for Kendall's tau but I can't say for sure.
Hope that helps!
SPSS tutorials
By Jorge Ortiz Pinilla on June 20th, 2020
Ruben Geert van den Berg, thank you very much for your answer. I'd like to be sure this difference reported is not due to a bug in SPSS programming. A 0.032 p.value should lead to rejecting the null hypothesis with the 0.05 significance level, but not if p.value = 0.067.
Which result can we trust?
Thank you again
Jorge Ortiz
By Ruben Geert van den Berg on June 21st, 2020
Hi Jorge!
I believe the NONPAR CORR p-value is the correct one. The issue is discussed in Kendall’s Tau in SPSS – 2 Easy Options but I don't have the time to read up on it.
Also, it's a good idea to download and install JASP (free and no spam). Whenever in doubt, double-check your results. You may find some surprises (like we did).
Hope that helps!
SPSS tutorials
By Kevin on July 28th, 2020
Hi Ruben,
Thank you for providing an online resource about Kendall’s Tau-B in SPSS:
My research includes seven continuous variables. I am trying to understand if each variable correlates with another variable at the neighborhood level---for example, a positive correlation between outdoor temperature and percentage of low-income individuals. We are not trying to predict a dependent variable from independent variables, but rather interested in the correlation (for the aforementioned example, this positive correlation would be a health inequity). I have a couple questions for you, if you don’t mind:
1. For performing the 21 separate bivariate correlations for the seven continuous variables, is it best practice to only use one type of correlation (i.e., Pearson, Spearman, Kendall) for all bivariate correlations, or should I be potentially using a mix of the three types, based on variable type, linearity, and normality? I ask, because most, but not all, of the data and relationships are non-normal, non-linear, and non-monotonic. Right now, I’m thinking of using Kendall’s Tau-B for all 21 bivariate correlations.
2. In your tutorial, you presented levels of strength of associations for Kendall’s Tau-B (0.07, 0.21, 0.35). Do you have any published resources that reference these levels of strength of associations? I hope to publish my research, and therefore require a source to cite. For Pearson Correlations, I see that Cohen (2008) has identified an absolute value of 0.1 as small, an absolute value of 0.3 as medium, and of 0.5 as large.
Cohen, J. (1988) Statistical Power Analysis for the Behavioral Sciences, 2nd ed. Hillsdale, NJ: Erlbaum.