• Example Data File
• Kendall’s Tau-B from Correlations Menu
• Kendall’s Tau-B & Tau-C from Crosstabs
• Wrong Significance Levels for Small Samples

Example Data File

A survey among company owners included the question “what was your yearly revenue?” for several years. The data -partly shown below- are in companies.sav.

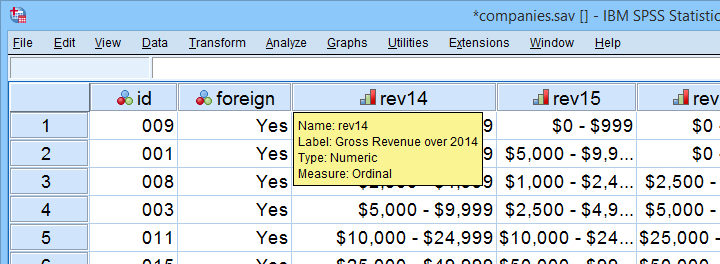
Our main research question for today is to what extent are yearly revenues interrelated? Are the best performing companies in 2014 the same as in 2015 and other years? Or do we have entirely different “winners” from year to year?
If we had the exact yearly revenues, we could have gone for Pearson correlation among years and perhaps proceed with some regression analyses.
However, our data contain only revenue categories and these are ordinal variables. This leaves us with 2 options: we can inspect either

• Spearman rank correlations or
• Kendall’s tau.

Although both statistics are appropriate, we'll go for Kendall’s tau: its standard error and sampling distribution are better known and the latter converges to a normal distribution faster.

Filtering Out Domestic Companies.

We'll restrict our analyses to foreign companies by using a FILTER. Since this variable only contains 1 (foreign) and 0 (domestic), a single line of syntax is all we need.

Kendall’s Tau-B from Correlations Menu

The easiest option for Kendalls tau-b is the correlations menu as shown below.

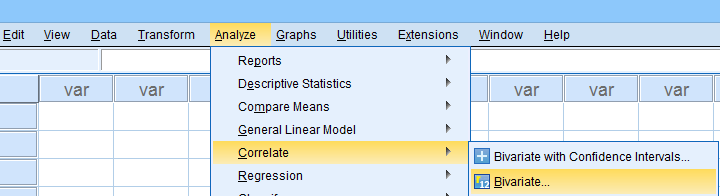
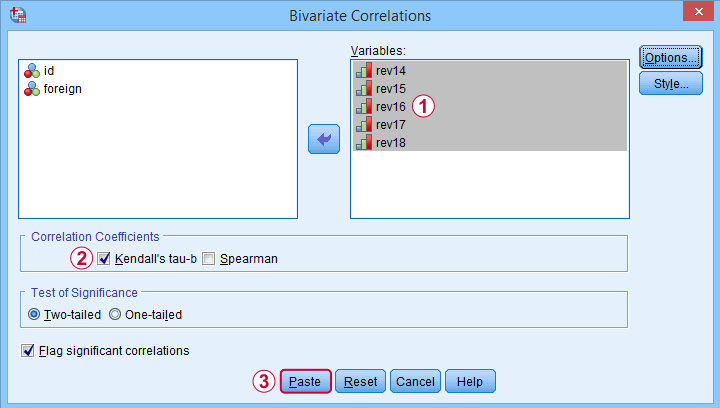
Move all relevant variables into the variables box,
select Kendall’s tau-b and
clicking Paste results in the syntax below. Let's run it.

Result

SPSS creates a full correlation matrix, part of which is shown below.

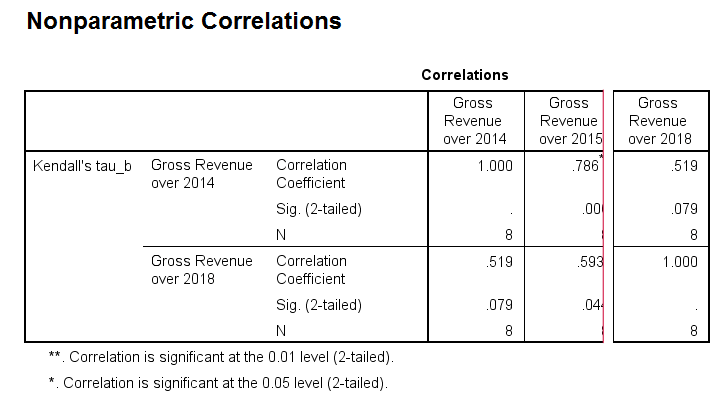
Note that most Kendall correlations are (very) high. This means that companies that perform well in one year
typically perform well in other years too. Despite our minimal sample size, many Kendall correlations are statistically significant. The p-values are identical to those obtained from rerunning the analysis in JASP.

Kendall’s Tau-B and Tau-C from Crosstabs

An alternative method for obtaining Kendalls tau from SPSS is from CROSSTABS. We only recommend this if

• you're going to run CROSSTABS anyway -probably for obtaining chi-square tests;
• you need Kendall’s tau-c instead of tau-b;

In such cases, you could access the Crosstabs dialog as shown below.

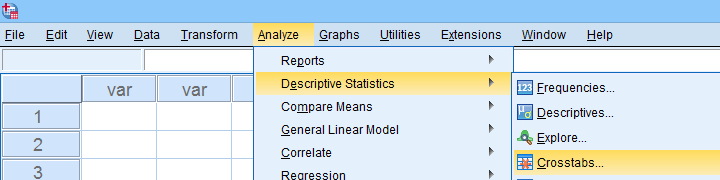
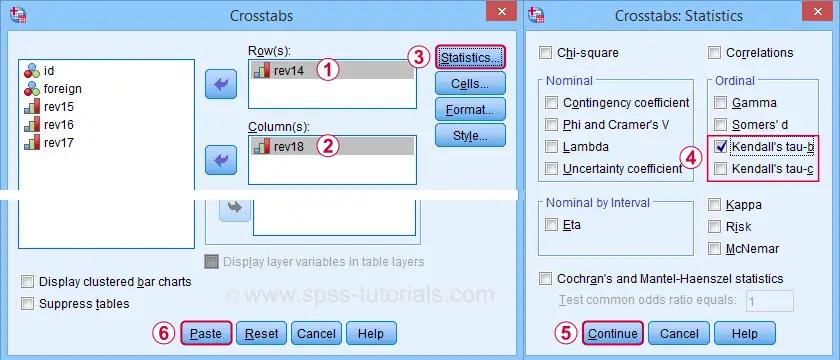
A lot of useful association measures -including Cramér’s V and eta squared- are found under Statistics.
Select either Kendall’s tau-b and/or tau-c -although the latter is rarely reported.
Clicking Paste results in the syntax below.

Wrong Significance Levels for Small Samples

Although Kendall’s tau obtained from CROSSTABS is correct, some of the other results are awkward at best.

Kendall’s tau-b is identical to that obtained from the correlations dialog;
The Approximate T is a z-value rather than a t-value: it's approximately normally distributed but only for reasonable sample sizes. It cannot be used for the small sample size used in this example.
As a result, the Approximate Significance is wildly off: SPSS comes up with p = 0.079 for the exact same data when using the correlations dialog. This is the exact p-value that should be used for small sample sizes.

“Officially”, the approximate significance may be used for N > 10 but perhaps it's better avoided if N < 20 or so. In such cases, it may be wiser to run Kendall’s tau from the Correlations dialog than from Crosstabs.

Thanks for reading.