A sampling distribution is the frequency distribution of a statistic over many random samples from a single population. Sampling distributions are at the very core of inferential statistics but poorly explained by most standard textbooks. The reasoning may take a minute to sink in but when it does, you'll truly understand common statistical procedures such as ANOVA or a chi-square test.
Sampling Distribution - Example
There's an island with 976 inhabitants. Its government has data on this entire population, including the number of times people marry. The screenshot below shows part of these data.

Population Distribution Marriages
Many inhabitants never married (yet), in which case marriages is zero. Other inhabitants married, divorced and remarried, sometimes multiple times. The histogram below shows the distribution of marriages over our 976 inhabitants.
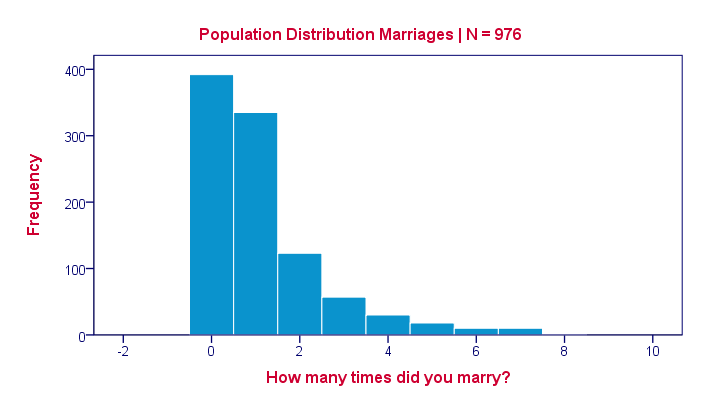
Note that the population distribution is strongly skewed (asymmetrical) which makes sense for these data. On average, people married some 1.1 times as shown by some descriptive statistics below.

These descriptives reemphasize the high skewness of the population distribution; the skewness is around 1.8 whereas a symmetrical distribution has zero skewness.
Sampling Distribution - What and Why
The government has these exact population figures. However, a social scientist doesn't have access to these data. So although the government knows, our scientist is clueless how often the island inhabitants marry. In theory, he could ask all 976 people and thus find the exact population distribution of marriages. Since this is too time consuming, he decides to draw a simple random sample of n = 10 people.
On average, the 10 respondents married 1.1 times. So what does this say about the entire population of 976 people? We can't conclude that they marry 1.1 times on average because a second sample of n = 10 will probably come up with a (slightly) different mean number of marriages.
This is basically the fundamental problem in inferential statistics: sample statistics vary over (hypothetical) samples. The solution to the problem is to figure out how much they vary. Like so, we can at least estimate a likely range -known as a confidence interval- for a population parameter such as an average number of marriages.
Sampling Distribution - Simulation Study
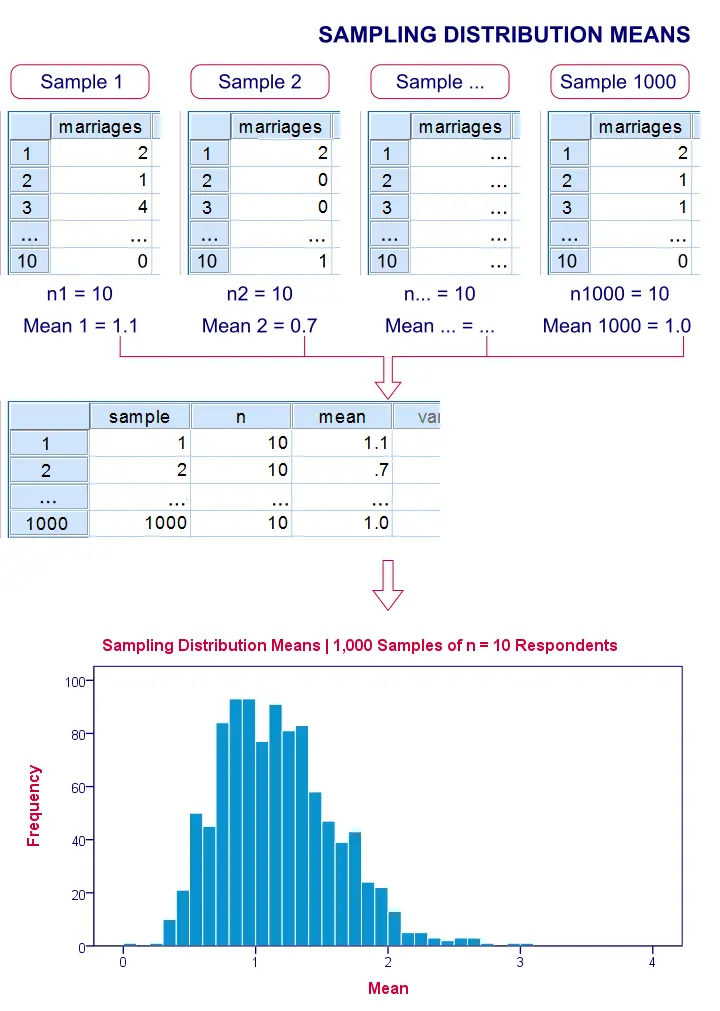
If we draw repeated samples of 10 respondents from our island population, then how much will the average number of marriages vary over such samples? One approach here is a computer simulation (the one below was done with SPSS).
We actually drew 1,000 samples of n = 10 respondents from our population data of 976 inhabitants. We then computed the average number of marriages in each of these samples. A histogram of the outcomes visualizes the sampling distribution: the distribution of a sample statistic over many repeated samples.
Sampling Distribution - Central Limit Theorem
The outcome of our simulation shows a very interesting phenomenon: the sampling distribution of sample means is very different from the population distribution of marriages over 976 inhabitants: the sampling distribution is much less skewed (or more symmetrical) and smoother.
In fact, means and sums are always normally distributed (approximately) for reasonable sample sizes, say n > 30. This doesn't depend on whatever population distribution the data values may or may not follow.It does, however, require independent and identically distributed variables, which is a common assumption for most applied statistics. This phenomenon is known as the central limit theorem.
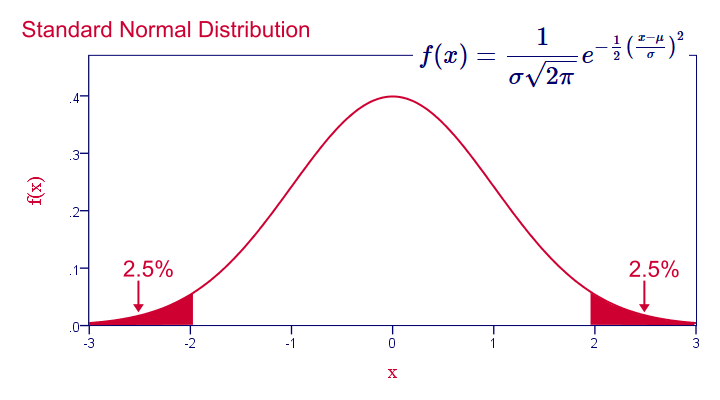
Note that even for 1,000 samples of n = 10, our sampling distribution of means is already looking somewhat similar to the normal distribution shown below.
Standard Normal Distribution
Common Sampling Distributions
The sampling distributions you'll encounter most in practice all derive from the normal distribution implied by the central limit theorem. This holds for
- the normal distribution for sample means, sums, percentages and proportions;
- the t distribution for sample means in a t-test and beta coefficients in regression analysis;
- the chi-square distribution for variances;
- the F-distribution for variance ratios in ANOVA.
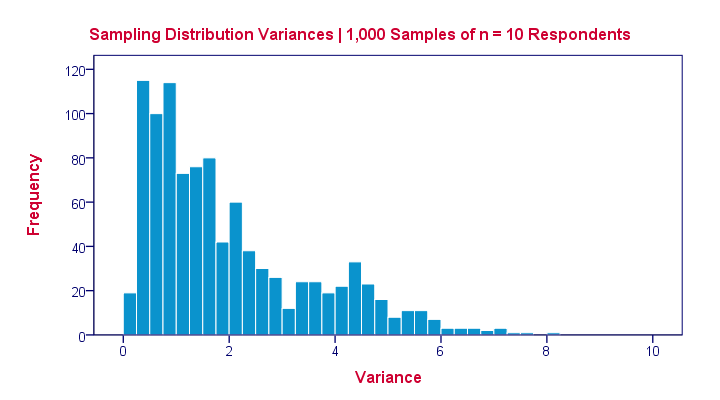 The sampling distribution for a variance approximates a chi-square distribution rather than a normal distribution.
The sampling distribution for a variance approximates a chi-square distribution rather than a normal distribution.
Sampling Distribution - Importance
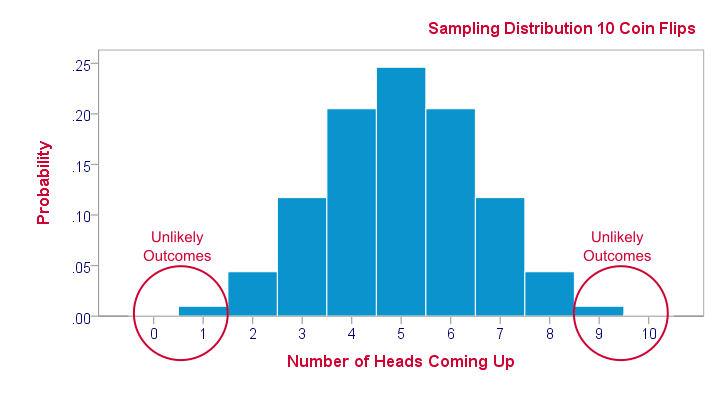
Sampling distributions tell us which outcomes are likely, given our research hypotheses. So perhaps our hypothesis is that a coin is balanced: both heads and tails have a 50% chance of landing up after a flip. This hypothesis implies the sampling distribution shown below for the number of heads resulting from 10 coin flips.

This tells us that from 1,000 such random samples of 10 coin flips, roughly 10 samples (1%) should result in 0 or 1 heads landing up. We therefore consider 0 or 1 heads an unlikely outcome. If such an outcome occurs anyway, then perhaps the coin wasn't balanced after all. We reject our hypothesis of equal chances for heads and tails and conclude that heads has a lower than 50% chance of landing up.
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 11 COMMENTS:
By Saleh on December 10th, 2018
I need book in sampling distribution.
By Ruben Geert van den Berg on December 11th, 2018
Hi Saleh!
What do you mean? A reference? More information? Please tell us what exactly you're looking for and we may come up with some suggestions.
Hope that helps!
SPSS tutorials
By Ramdani on December 14th, 2018
Good!
By liat on September 6th, 2022
Hi
Such a vivid explanation, but statistics are no walk in the park. I hope you can clarify my confusion.
In light of the fact that all statistics are based on the central limit theorem and that the population is not always normally distributed, and that only averages and sums of many samples converge to a normal distribution, so that conclusions can be drawn about the population- so why is there a difference between parametric and non-parametric testing?
According to the argument, parametric tests are chosen since the sample or population is assumed to have a non-normal distribution. The argument is essentially the same as that made in the previous paragraph regarding non-parametric tests, is it not?
Is the reason for choosing parametric tests solely based on the type of dependent variables ( ordinal or higher) and the size of the sample?
Do all statistical tests (parametric and non-parametric) provide significant (or not) results about the population?
In the Chi-square test, when comparing the expected probability (which is calculated from the sample) with the sample measure, why does it suffice to draw conclusions about the population rather than just the sample?
I have one last question. In your opinion, if someone performed a Kruskal Wallis for five groups with a binary gender dependent variable (binary) or another categorical variable with more than two values, and compared the group distributions, would he receive nonsense results because the dependent variable is not of order type or higher?
I would appreciate any assistance you can provide.
By Ruben Geert van den Berg on September 7th, 2022
I totally understand your confusion.
First off, "nonparametric tests" usually misrefer to distribution free tests -something completely different.
A distribution free test is a test that does not require distributional assumptions such as population normality or equal population variances. Distribution free tests do -however- involve sampling distributions (normal/chi-square/...) for arriving at p-values.
You should really use distribution free tests if
-outcome variables are ordinal and/or
-sample sizes are small (each n < 25 or so) If neither condition holds, the central limit theorem renders most tests robust against even severe violations of normality. Sadly, even most instructors don't understand this and that's the main reason why people use (pretty worthless) normality tests such as -the Kolmogorov-Smirnov test and
-the Shapiro-Wilk test.
Regarding your last question, Kruskal Wallis seems a poor choice because gender will be full of ties (only 2 values). Just use a chi-square independence test if the groups are nominal.
If the groups are ordinal, consider a Spearman rank correlation.
Hope that helps!
SPSS tutorials
P.s. one of the few books that gets these things right is Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.