Also see Binomial Test - Simple Tutorial for a quick explanation of how this test works.
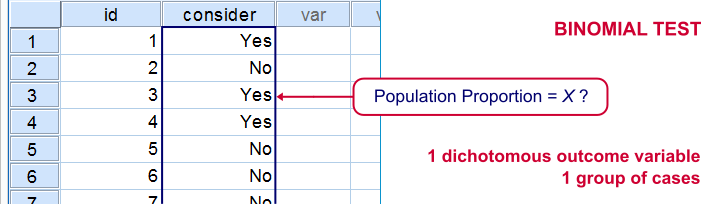
SPSS binomial test is used for testing whether a proportion from a single dichotomous variable is equal to a presumed population value. The figure illustrates the basic idea.
SPSS Binomial Test Example
A biologist claims that 75% of a population of spiders consist of female spiders. With a lot of effort he collects 15 spiders, 7 of which are female. These data are in spiders.sav, part of which are shown below.
1. Quick Data Check
Let's first take a quick look at the FREQUENCIES
for gender. Like so, we can inspect whether there are any missing values and whether the variable is really dichotomous. We'll run some FREQUENCIES. The syntax is so simple that we'll just type it instead of clicking through the menu.
frequencies gender.

The output tells us that there are no missing values and the variable is indeed dichotomous. We can proceed our analysis with confidence.
2. Assumptions Binomial Test
The results from any statistical test can only be taken seriously insofar as its assumptions have been met. For the binomial test we need just one:
- independent observations (or, more precisely, independent and identically distributed variables);
This assumption is beyond the scope of this tutorial. We presume it's been met by the data at hand.
3. Run SPSS Binomial Test
We'd like to test whether the proportion of female spiders differs from .75 (our test proportion). Now SPSS Binomial Test has a very odd feature: the test proportion we enter applies to the category that's first encountered in the data. So the hypothesis that's tested depends on the order of the cases. Because our test proportion applies to female (rather than male) spiders, we need to move our female spiders to the top of the data file. We'll do so by running the syntax below. Next, we'll run the actual binomial test.
sort cases by gender.
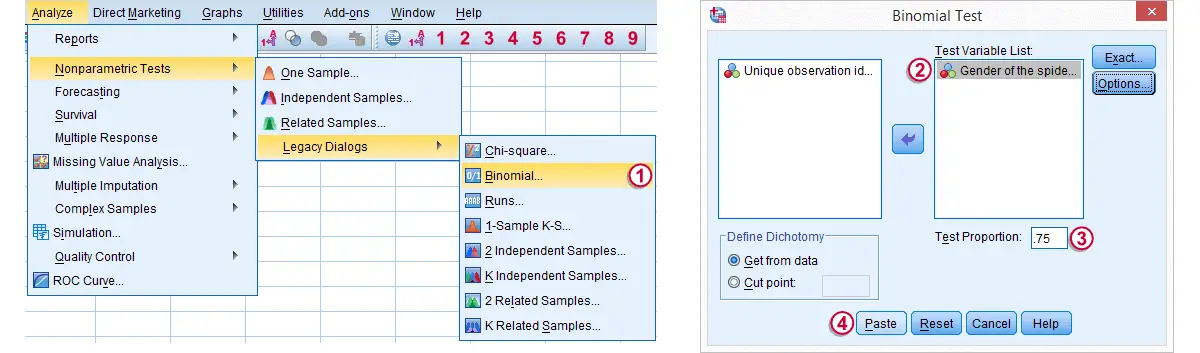
 Clicking results in the syntax below. We'll run it and move on the output.
Clicking results in the syntax below. We'll run it and move on the output.
NPAR TESTS
/BINOMIAL (.75)=gender
/MISSING ANALYSIS.
4. SPSS Binomial Test Output

 Since we have 7 female spiders out of 15 observations, the observed proportion is (7 / 15 =) .47.
Since we have 7 female spiders out of 15 observations, the observed proportion is (7 / 15 =) .47.
 Our null hypothesis states that this proportion is .75 for the entire population.
Our null hypothesis states that this proportion is .75 for the entire population.
 The p value, denoted by Exact Sig. (1-tailed) is .017. If the proportion of female spiders is exactly .75 in the entire population, then there's only a 1.7% chance of finding 7 or fewer female spiders in a sample of N = 15. We often reject the null hypothesis if this chance is smaller than 5% (p < .05). We conclude that the proportion of female spiders is not .75 in the population but probably (much) lower.
The p value, denoted by Exact Sig. (1-tailed) is .017. If the proportion of female spiders is exactly .75 in the entire population, then there's only a 1.7% chance of finding 7 or fewer female spiders in a sample of N = 15. We often reject the null hypothesis if this chance is smaller than 5% (p < .05). We conclude that the proportion of female spiders is not .75 in the population but probably (much) lower.
Note that the p value is the chance of finding the observed proportion or a “more extreme” outcome. If the observed proportion is smaller than the test proportion, then a more extreme outcome is an even smaller proportion than the one we observe.The reasoning is entirely reversed when the observed proportion is larger than the expected proportion. We ignore the fact that finding very large proportions would also contradict our null hypothesis. This is what's meant by (1-tailed).A 2-tailed binomial test is only be applied when the test proportion is exactly .5. The (rather technical) reason for this is that the binomial sampling distribution for the observed proportion is only symmetrical in the latter case.
5. Reporting a Binomial Test
When reporting test results, we always report some descriptive statistics as well. In this case, a frequency table will do. Regarding the significance test, we'll write something like “a binomial test indicated that the proportion of female spiders of .47 was lower than the expected .75, p = .017 (1-sided)”.
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 36 COMMENTS:
By Sergej on May 12th, 2017
Section 4: The significance value from SPSS is NOT the p-value in the common sense. It is *half* the p-value (statement "1-tailed" explicitly points to this). So in the given example, we should compare the significance level 0.05 with 2*0.017=0.034.
By Ruben Geert van den Berg on May 12th, 2017
Hi Sergej!
First off, a p-value and "Significance" in SPSS are the very same thing. In fact, if I'd own SPSS, I'd replace all instances of "Significance" by "p". Unfortunately, I don't own SPSS -not yet, anyway.
Now, many statistical tests provide a 1-tailed and a 2-tailed p-value but the one to be reported is often open to discussion. I agree with you that 2-tailed p-values are always preferable over their 1-tailed counterparts but you'll find both in the literature.
Not sure you saw it but the second hidden note in this section says
"A 2-tailed binomial test is only applied when the test proportion is exactly .5. The (rather technical) reason for this is that the binomial sampling distribution for the observed proportion is only symmetrical in the latter case."
Since our test proportion is not 0.5 here, there's no such thing as a "2-sided p-value" for this test. It's undefined. You cannot simply multiply the p-value by 2 here as you do with a t-test.
Hope that helps!
Ruben
By oscar romero on July 2nd, 2018
The explanation of how the binomial test works is very good. Very good example Thank you
By carl on September 19th, 2018
When there is just 6 spiders in our sample, and in a special situation we expect that all of them should be females. Is it possible to use Binomial Test or the Exact Binomial Test by choosing test proportion of 0.999 ?
By Ruben Geert van den Berg on September 20th, 2018
This wouldn't make sense. If we expect that all spiders are female, then we must reject this null hypothesis whenever we find at least 1 male spider. If we find at least one male spider, p = 0.000. There's a zero chance of finding a male spider if they're all female. We don't even need any statistical significance test for this conclusion.