For reading up on some basics, see Chi-Square Independence Test - Quick Introduction.
Null Hypothesis for the Chi-Square Independence Test

A chi-square independence test evaluates if two categorical variables are associated in some population. We'll therefore try to refute the null hypothesis that
two categorical variables are (perfectly) independent in some population.
If this is true and we draw a sample from this population, then we may see some association between these variables in our sample. This is because samples tend to differ somewhat from the populations from which they're drawn.
However, a strong association between variables is unlikely to occur in a sample if the variables are independent in the entire population. If we do observe this anyway, we'll conclude that the variables probably aren't independent in our population after all. That is, we'll reject the null hypothesis of independence.
Example
A sample of 183 students evaluated some course. Apart from their evaluations, we also have their genders and study majors. The data are in course_evaluation.sav, part of which is shown below.
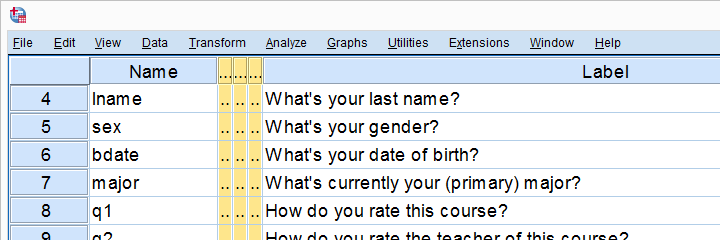
We'd now like to know: is study major associated with gender? And -if so- how? Since study major and gender are nominal variables, we'll run a chi-square test to find out.
Assumptions Chi-Square Independence Test
Conclusions from a chi-square independence test can be trusted if two assumptions are met:
- independent observations. This usually -not always- holds if each case in SPSS holds a unique person or other statistical unit. Since this is that case for our data, we'll assume this has been met.
- For a 2 by 2 table, all expected frequencies > 5.If you've no idea what that means, you may consult Chi-Square Independence Test - Quick Introduction. For a larger table, no more than 20% of all cells may have an expected frequency < 5 and all expected frequencies > 1.
SPSS will test this assumption for us when we'll run our test. We'll get to it later.
Chi-Square Independence Test in SPSS
In SPSS, the chi-square independence test is part of the CROSSTABS procedure which we can run as shown below.
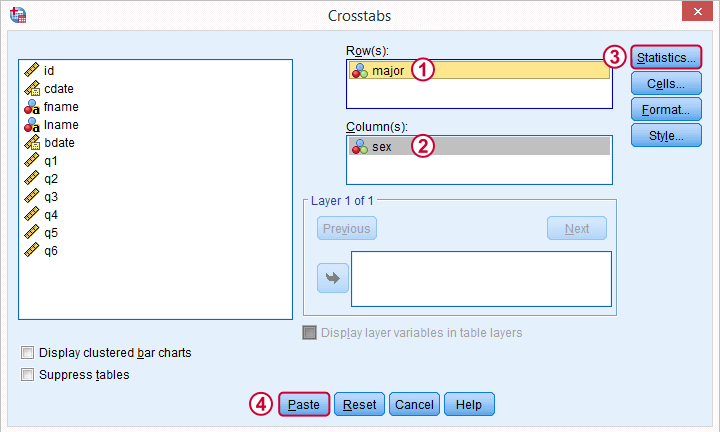
In the main dialog, we'll enter one variable into the box and the other into . Since sex has only 2 categories (male or female), using it as our column variable results in a table that's rather narrow and high. It will fit more easily into our final report than a wider table resulting from using major as our column variable. Anyway, both options yield identical test results.
 Under we'll just select . Clicking results in the syntax below.
Under we'll just select . Clicking results in the syntax below.
SPSS Chi-Square Independence Test Syntax
CROSSTABS
/TABLES=major BY sex
/FORMAT=AVALUE TABLES
/STATISTICS=CHISQ
/CELLS=COUNT
/COUNT ROUND CELL.
You can use this syntax if you like but I personally prefer a shorter version shown below. I simply type it into the Syntax Editor window, which for me is much faster than clicking through the menu. Both versions yield identical results.
crosstabs major by sex
/statistics chisq.
Output Chi-Square Independence Test

First off, we take a quick look at the Case Processing Summary to see if any cases have been excluded due to missing values. That's not the case here. With other data, if many cases are excluded, we'd like to know why and if it makes sense.
Contingency Table

Next, we inspect our contingency table. Note that its marginal frequencies -the frequencies reported in the margins of our table- show the frequency distributions of either variable separately.
Both distributions look plausible and since there's no “no answer” categories, there's no need to specify any user missing values.
Significance Test

 First off, our data meet the assumption of all expected frequencies > 5 that we mentioned earlier. Since this holds, we can rely on our significance test for which we use Pearson Chi-Square.
First off, our data meet the assumption of all expected frequencies > 5 that we mentioned earlier. Since this holds, we can rely on our significance test for which we use Pearson Chi-Square.
Right, we usually say that the association between two variables is statistically significant if Asymptotic Significance (2-sided) < 0.05 which is clearly the case here.
Significance is often referred to as “p”, short for probability; it is the probability of observing our sample outcome if our variables are independent in the entire population. This probability is 0.000 in our case. Conclusion: we reject the null hypothesis that our variables are independent in the entire population.
Understanding the Association Between Variables
We conclude that our variables are associated but what does this association look like? Well, one way to find out is inspecting either column or row percentages. I'll compute them by adding a line to my syntax as shown below.
set tvars labels tnumbers labels.
*Crosstabs with frequencies and row percentages.
crosstabs major by sex
/cells count row
/statistics chisq.
Adjusting Our Table
Since I'm not too happy with the format of my newly run table, I'll right-click it and select

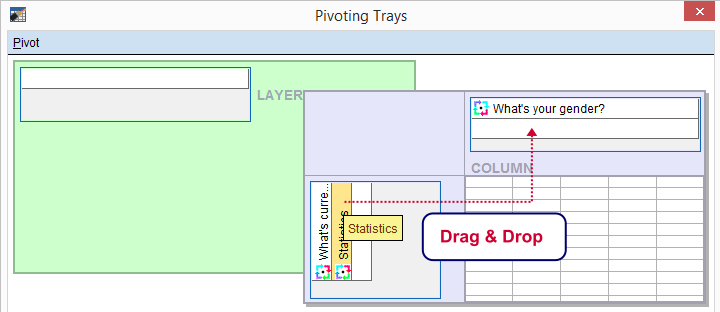
We select and then drag and drop right underneath “What's your gender?”. We'll close the pivot table editor.
Result

Roughly half of our sample if female. Within psychology, however, a whopping 87% is female. That is, females are highly overrepresented among psychology students. Like so, study major “says something” about gender: if I know somebody studies psychology, I know she's probably female.
The opposite pattern holds for economy students: some 80% of them are male. In short, our row percenages describe the association we established with our chi-square test.
We could quantify the strength of the association by adding Cramér’s V to our test but we'll leave that for another day.
Reporting a Chi-Square Independence Test
We report the significance test with something like “an association between gender and study major was observed, χ2(4) = 54.50, p = 0.000. Further, I suggest including our final contingency table (with frequencies and row percentages) in the report as well as it gives a lot of insight into the nature of the association.
So that's about it for now. Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 72 COMMENTS:
By Martin F. Sherman on November 8th, 2014
You indicate that the probability of the chi squared test is equal to .000 which you then state "that there's a 0% change to find the observed (or large) degree of association between the variables." This is not exactly correct. The reason the p value is equal .000 is that spss only carried the p value to three decimal places. If you up actually carried the p value out further you would discover that the p value is not equal to .000. It is impossible for the p value to be exactly equal to .000. All of statistically testing is based on probability and theoretical distributions that are asymptomatic to the X axis. Hence, no such thing as a p value equal .000 and that there's 0% chance.
By Ruben Geert van den Berg on November 10th, 2014
Thank you for you feedback. You're correct that non zero decimals may be present in the p value presented as .000. Perhaps "a close to 0% chance" would have been better here. Then again, you could argue that -scientifically speaking- "0%" could mean anything between -.5% and .5%. Note that I didn't write "exactly 0%". I'm aiming at being as brief as possible in these tutorials and I'm actually working on some more detailed ones in which I'll go into theoretical detail a bit more.
With regard to your last remark: note that some statistical tests (such as the binomial test) use a probability distribution rather than a density function. There's nothing asymptotic about a binomial distribution.
By Ounsa on March 16th, 2015
What variables shall I put in the raws and what variables shall I put in the colums
By Ruben Geert van den Berg on March 16th, 2015
The chi-square test results are not affected by swapping rows and columns. You can choose the option here that's most conventient for you, which may depend on the number of categories in either variable and the question you're aiming to answer.
By Paul-Anthony Kweku somiah on August 5th, 2015
It is very tactful tutorial and that it continues for more researcher to benefit from especially student researchers.