• Method I - Histograms
• Excluding Outliers from Data
• Method II - Boxplots
• Method III - Z-Scores (with Reporting)
• Method III - Z-Scores (without Reporting)

Summary

Outliers are basically values that fall outside of a normal range for some variable. But what's a “normal range”? This is subjective and may depend on substantive knowledge and prior research. Alternatively, there's some rules of thumb as well. These are less subjective but don't always result in better decisions as we're about to see.

In any case: we usually want to exclude outliers from data analysis. So how to do so in SPSS? We'll walk you through 3 methods, using life-choices.sav, partly shown below.

In this tutorial, we'll find outliers for these reaction time variables.

During this tutorial, we'll focus exclusively on reac01 to reac05, the reaction times in milliseconds for 5 choice trials offered to the respondents.

Method I - Histograms

Let's first try to identify outliers by running some quick histograms over our 5 reaction time variables. Doing so from SPSS’ menu is discussed in Creating Histograms in SPSS. A faster option, though, is running the syntax below.

Result

Let's take a good look at the first of our 5 histograms shown below.

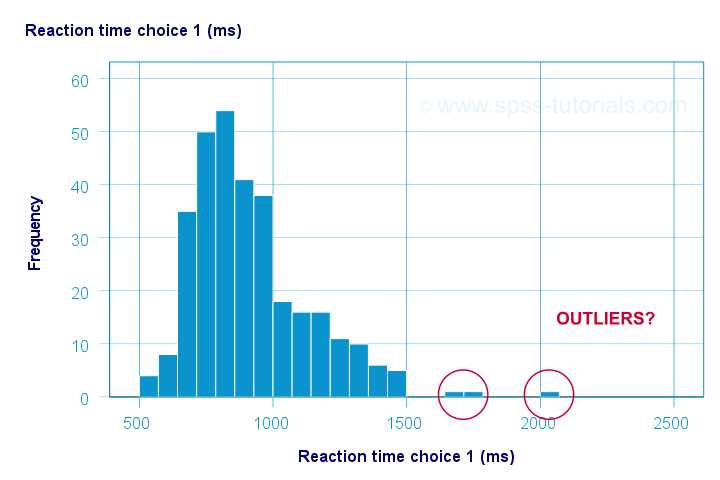
The “normal range” for this variable seems to run from 500 through 1500 ms. It seems that 3 scores lie outside this range. So are these outliers? Honestly, different analysts will make different decisions here. Personally, I'd settle for only excluding the score ≥ 2000 ms. So what's the right way to do so? And what about the other variables?

Excluding Outliers from Data

The right way to exclude outliers from data analysis is to specify them as user missing values. So for reaction time 1 (reac01), running missing values reac01 (2000 thru hi). excludes reaction times of 2000 ms and higher from all data analyses and editing. So what about the other 4 variables?

The histograms for reac02 and reac03 don't show any outliers.

For reac04, we see some low outliers as well as a high outlier. We can find which values these are in the bottom and top of its frequency distribution as shown below.

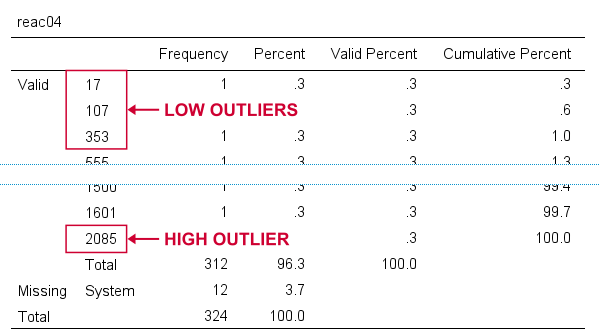If we see any outliers in a histogram, we may look up the exact values in the corresponding frequency table.

We can exclude all of these outliers in one go by running missing values reac04 (lo thru 400,2085). By the way: “lo thru 400” means the lowest value in this variable (its minimum) through 400 ms.

For reac05, we see several low and high outliers. The obvious thing to do seems to run something like missing values reac05 (lo thru 400,2000 thru hi). But sadly, this only triggers the following error:

The problem here is that you can't specify a low and a high
range of missing values in SPSS. Since this is what you typically need to do, this is one of the biggest stupidities still found in SPSS today. A workaround for this problem is to

• RECODE the entire low range into some huge value such as 999999999;
• add the original values to a value label for this value;
• specify only a high range of missing values that includes 999999999.

The syntax below does just that and reruns our histograms to check if all outliers have indeed been correctly excluded.

Result

First off, note that none of our 5 histograms show any outliers anymore; they're now excluded from all data analysis and editing. Also note the bottom of the frequency table for reac05 shown below.

Low outliers after recoding and labelling are listed under Missing.

Even though we had to recode some values, we can still report precisely which outliers we excluded for this variable due to our value label.

Before proceeding to boxplots, I'd like to mention 2 worst practices for excluding outliers:

• removing outliers by changing them into system missing values. After doing so, we no longer know which outliers we excluded. Also, we're clueless why values are system missing as they don't have any value labels.
• removing entire cases -often respondents- because they have 1(+) outliers. Such cases typically have mostly “normal” data values that we can use just fine for analyzing other (sets of) variables.

Sadly, supervisors sometimes force their students to take this road anyway. If so, SELECT IF permanently removes entire cases from your data.

Method II - Boxplots

If you ran the previous examples, you need to close and reopen life-choices.sav before proceeding with our second method.

We'll create a boxplot as discussed in Creating Boxplots in SPSS - Quick Guide: we first navigate to Analyze Descriptive Statistics Explore as shown below.

Next, we'll fill in the dialogs as shown below.

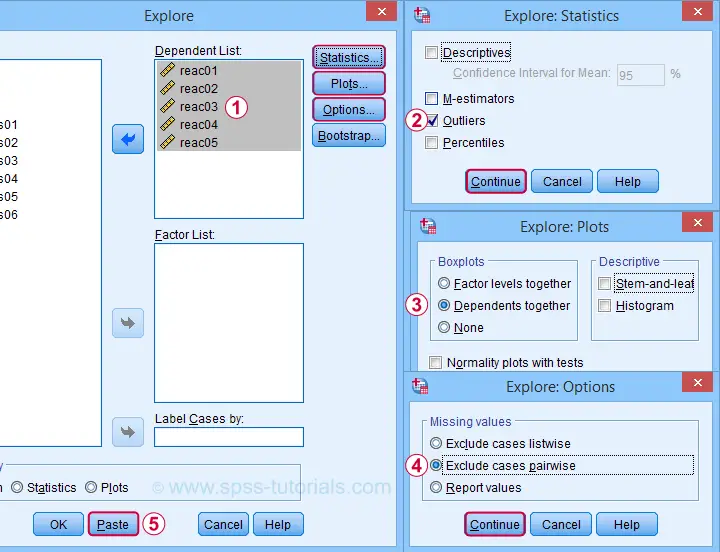
Completing these steps results in the syntax below. Let's run it.

Result

Quick note: if you're not sure about interpreting boxplots, read up on Boxplots - Beginners Tutorial first.

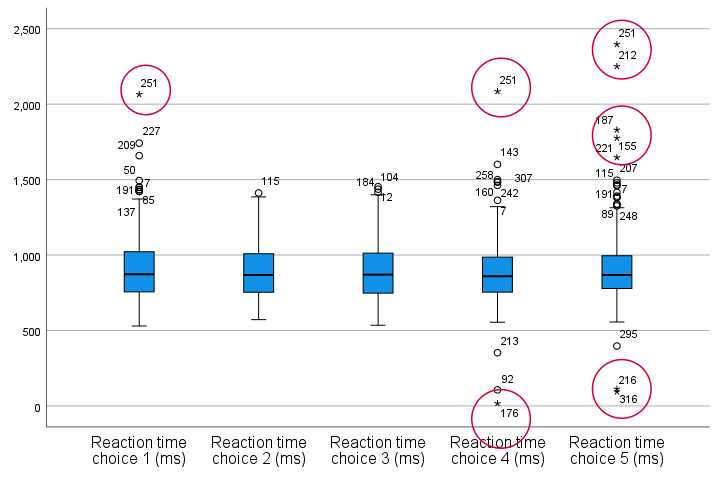
Our boxplot indicates some potential outliers for all 5 variables. But let's just ignore these and exclude only the extreme values that are observed for reac01, reac04 and reac05.

So, precisely which values should we exclude? We find them in the Extreme Values table. I like to copy-paste this into Excel. Now we can easily boldface all values that are extreme values according to our boxplot.

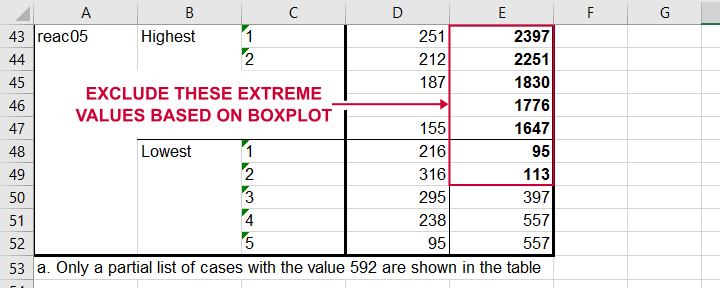Copy-pasting the Extreme Values table into Excel allows you to easily boldface the exact outliers that we'll exclude.

Finally, we set these extreme values as user missing values with the syntax below. For a step-by-step explanation of this routine, look up Excluding Outliers from Data.

Method III - Z-Scores (with Reporting)

A common approach to excluding outliers is to look up which values correspond to high z-scores. Again, there's different rules of thumb which z-scores should be considered outliers. Today, we settle for |z| ≥ 3.29 indicates an outlier. The basic idea here is that if a variable is perfectly normally distributed, then only 0.1% of its values will fall outside this range.

So what's the best way to do this in SPSS? Well, the first 2 steps are super simple:

• we add z-scores for all relevant variables to our data and
• see if their minima or maxima meet |z| ≥ 3.29.

Funnily, both steps are best done with a simple DESCRIPTIVES command as shown below.

Result

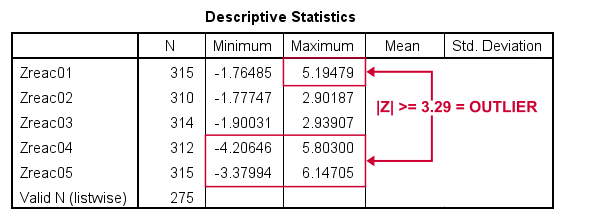Minima and maxima for our newly computed z-scores.

Basic conclusions from this table are that

• reac01 has at least 1 high outlier;
• reac02 and reac03 don't have any outliers;
• reac04 and reac05 both have at least 1 low and 1 high outlier.

But which original values correspond to these high absolute z-scores? For each variable, we can run 2 simple steps:

• FILTER away cases having |z| < 3.29 (all non outliers);
• run a frequency table -now containing only outliers- on the original variable.

The syntax below does just that but uses TEMPORARY and SELECT IF for filtering out non outliers.

Result

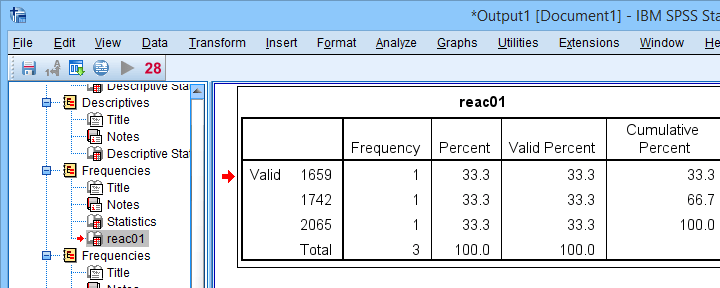Finding outliers by filtering out all non outliers based on their z-scores.

Note that each frequency table only contains a handful of outliers for which |z| ≥ 3.29. We'll now exclude these values from all data analyses and editing with the syntax below. For a detailed explanation of these steps, see Excluding Outliers from Data.

Method III - Z-Scores (without Reporting)

We can greatly speed up the z-score approach we just discussed but this comes at a price: we won't be able to report precisely which outliers we excluded. If that's ok with you, the syntax below almost fully automates the job.

Result

The frequency table below tells us that 4 outliers having |z| ≥ 3.29 were excluded for reac04.

Under Missing we see the number of excluded outliers but not the exact values.

Sadly, we're no longer able to tell precisely which original values these correspond to.

Final Notes

Thus far, I deliberately avoided the discussion precisely which values should be considered outliers for our data. I feel that simply making a decision and being fully explicit about it is more constructive than endless debate.

I therefore blindly followed some rules of thumb for the boxplot and z-score approaches. As I warned earlier, these don't always result in good decisions: for the data at hand, reaction times below some 500 ms can't be taken seriously. However, the rules of thumb don't always exclude these.

As for most of data analysis, using common sense is usually a better idea...

Thanks for reading!