A boxplot is a chart showing quartiles, outliers and
the minimum and maximum scores for 1+ variables.

• Quartiles
• Interquartile Range - IQR
• Potential Outliers
• Extreme Values
• Boxplots or Histograms?

Example

A sample of N = 233 people completed a speedtask. The chart below shows a boxplot of their reaction times.

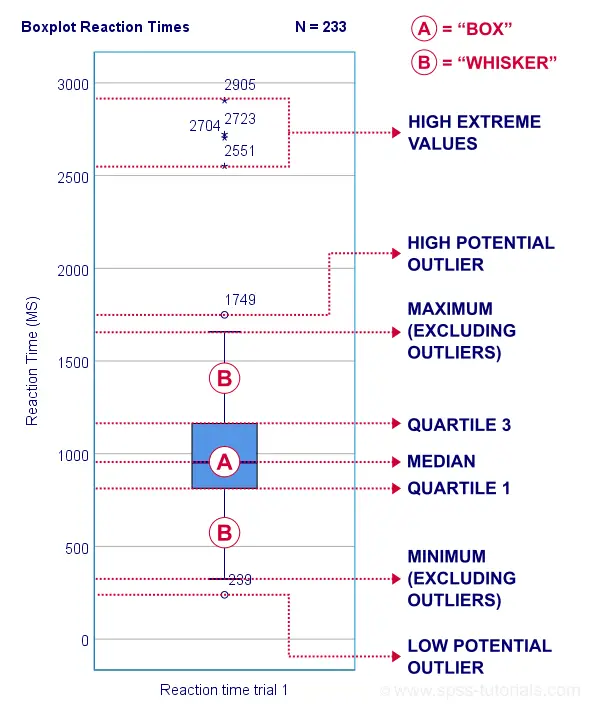
Some rough conclusions from this chart are that

• all 233 reaction times lie between 0 and 3,000 milliseconds;
• 4 scores are high extreme values. These are reaction times between 2,551 and 2,905 milliseconds;
• there's 1 high potential outlier of 1,749 milliseconds;
• the maximum reaction time (excluding potential outliers and extreme values) is around 1,650 milliseconds;
• 75% of all respondents score lower than some 1,150 milliseconds. This is the 75th percentile or quartile 3;
• 50% of all respondents score lower than some 975 milliseconds. This is the 50th percentile (the median) or quartile 2;
• 25% of all respondents score lower than some 800 milliseconds. This is the 25th percentile or quartile 1;
• the minimum reaction time (excluding potential outliers and extreme values) is around 350 milliseconds;
• there's 1 low potential outlier of 239 milliseconds;
• there aren't any low extreme values.

So what are quartiles? And how to obtain them? And how are potential outliers and extreme values defined?

We'll show you all you need to know in this Googlesheet, part of which is shown below.

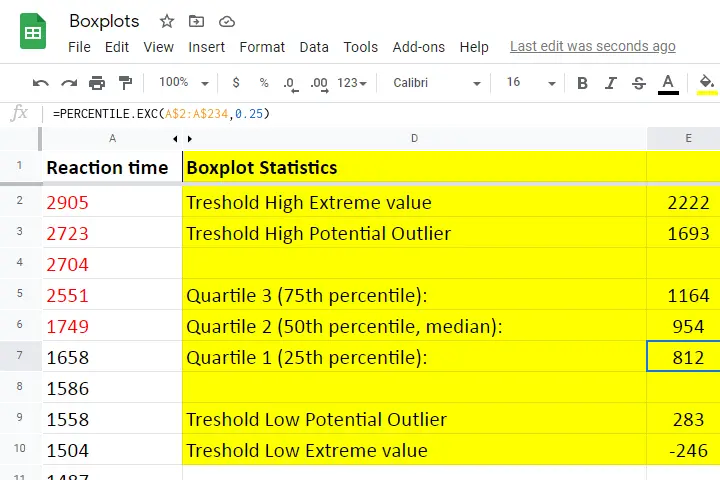
Quartile 1

Quartile 1 is the 25th percentile: it is the score that separates the lowest 25% from the highest 75% of scores. In Googlesheets and Excel, =PERCENTILE.EXC(A2:A234,0.25) returns quartile 1 for the scores in cells A2 through A234 (our 233 reaction times). The result is 811.5. This means that 25% of our scores are lower than 811.5 milliseconds. Or -reversely- 75% are higher.

A minor complication here is that 25% of N = 233 scores results in 58.25 scores. As there's no such thing as “0.25 scores”, we can't precisely separate the lowest 25% from the highest 75%.
There's no real solution to this problem but a technique known as linear interpolation probably comes closest. This is how Excel, Googlesheets and SPSS all come up with 811.5 as quartile 1 for our 233 scores.

Quartile 2

Quartile 2 -also known as the median- is the 50th percentile: the score that separates the lowest 50% from the highest 50% of scores. In Googlesheets, =PERCENTILE.EXC(A2:A234,0.50) returns quartile 2 for the scores in cells A2 through A234. For these data, that'll be 954 milliseconds.

This median is a measure of central tendency: it tells us that people typically had a reaction time of 954 milliseconds. Common measures of central tendency are

• the mean;
• the median;
• the mode.

Percentiles, quartiles and measures of central tendency can be obtained from SPSS’ Frequencies dialog.

Quartile 3

Quartile 3 is the 75th percentile: the score that separates the lowest 75% from the highest 25% of scores. In Googlesheets, =PERCENTILE.EXC(A2:A234,0.75) returns quartile 3 for the scores in cells A2 through A234. For our 233 reaction times, that'll be 1,164 milliseconds.

The screenshot below shows that SPSS comes up with the exact same quartiles as Excel and Googlesheets. We'll now use quartiles 1 and 3 (811.5 and 1,164 milliseconds) for computing the interquartile range or IQR.

SPSS comes up with identical quartiles for our N = 233 reaction times

Interquartile Range - IQR

The interquartile range or IQR is computed as

$$IQR = quartile\;3 - quartile\;1$$

so for our data, that'll be

$$IQR = 1,164 - 811.5 = 352.5$$

The IQR is a measure of dispersion: it tells how far data points typically lie apart. Common measures of dispersion are

• the standard deviation
• the variance;
• the IQR;
• the range.

Measures of dispersion in SPSS’ Frequencies dialog.

Potential Outliers

In boxplots, potential outliers are defined as follows:

• low potential outlier: score is more than 1.5 IQR but at most 3 IQR below quartile 1;
• high potential outlier: score is more than 1.5 IQR but at most 3 IQR above quartile 3.

For our data at hand, quartile 1 = 811.5 and the IQR = 352.5. Therefore, the thresholds for low potential outliers are

• upper bound: 811.5 - 1.5 * 352.5 = 282.8;
• lower bound: 811.5 - 3 * 352.5 = -246.0.

Scores that are smaller than this lower bound are considered low extreme values: these are scores even more than 3 IQR below quartile 1.

Thresholds for high potential outliers are computed in a similar fashion, using quartile 3 and the IQR. To sum things up: for our data at hand, thresholds for potential outliers are

• low potential outlier: -246 ≤ reaction time < 282.8 (milliseconds);
• high potential outlier: 1,692.8 < reaction time ≤ 2,221.5 (milliseconds).

As shown in our boxplot example, potential outliers are typically shown as circles. These either lie below the minimum or above the maximum (both excluding outliers).

A final note here is that these definitions apply only to boxplots. In other contexts, z-scores are often used to define outliers.

Extreme Values

For boxplots, extreme values are defined as follows:

• low extreme value: score is more than 3 IQR below quartile 1;
• high extreme value: score is more than 3 IQR above quartile 3.

For our 233 reaction times, this implies

• low extreme value: reaction time < -246 (milliseconds);
• high extreme value: reaction time > 2,221.5 (milliseconds).

In boxplots, extreme values are usually indicated by asterisks (*). Note that our example boxplot shows 4 high extreme values but no low extreme values.

Boxplots - Purposes

Basic purposes of boxplots are

• quick and simple data screening, especially for outliers and extreme values;
• comparing 2+ variables for 1 sample (within-subjects test);
• comparing 2+ samples on 1 variable (between-subjects test).

The figure below shows a quick boxplot comparison among 3 samples (age groups) on 1 variable (reaction time trial 3).

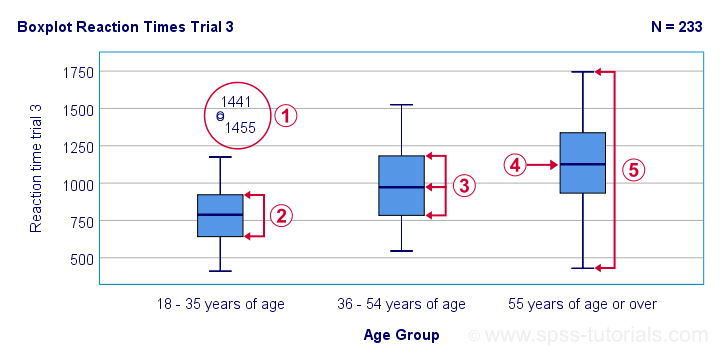
The youngest age group has 2 potential outliers. However, they don't look too bad as they'd fall in the normal range for the other age groups.
The young age group has the lowest “box”. This indicates that these respondents have the smallest IQR. Since the IQR ignores the bottom and top 25% of scores, this group does not necessarily have the smallest standard deviation too.
The median lies roughly midway between quartiles 1 and 3. This suggests a roughly symmetrical frequency distribution.
The oldest age group has the highest median reaction time and reversely. Respondents thus seem to get slower with increasing age.
Reaction time for the oldest respondents have the largest range: the scores seem to lie further apart insofar as respondents are older.

Boxplots or Histograms?

Histograms.

The figure below illustrates why I always prefer histograms over boxplots. It's based on the exact same data as our last boxplot example.

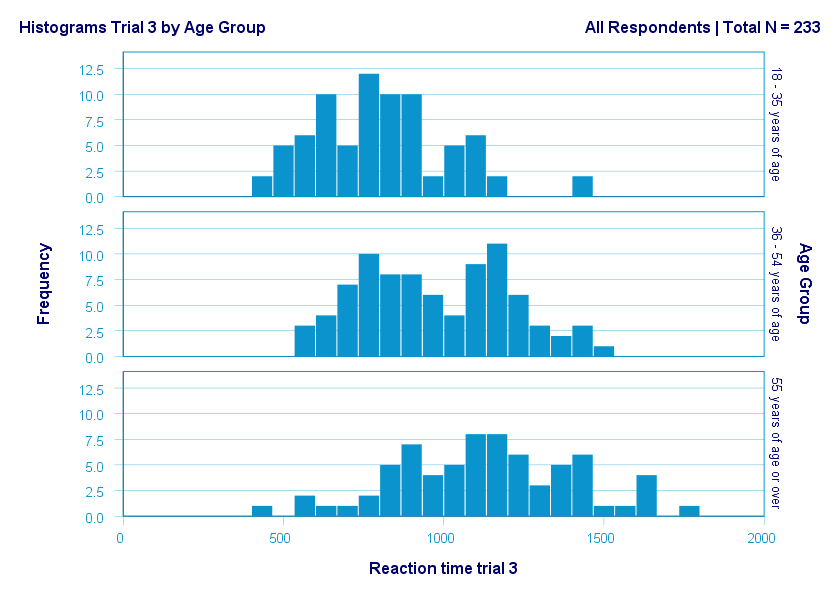
So what did the boxplot tell us that this histogram doesn't? Well, nothing really. Does it? Reversely, however, the histogram tells us that

• reaction times seem to follow a bimodal distribution for the intermediate age group;
• this distribution is therefore flattened (platykurtic) relative to a normal distribution. To some extent, this also holds for the other 2 age groups;
• means as well as standard deviations seem to increase with increasing age.

Our histograms make these points much clearer than our boxplot: in boxplots, we can't see how scores are distributed within the “box” or between the “whiskers”.
A histogram, however, allows us to roughly reconstruct our original data values. A chart simply doesn't get any more informative than that.

Agree? Disagree? Throw me a comment below and let me know what you think.

Thanks for reading!