Also see One-Sample T-Test - Quick Tutorial & Example.

SPSS one-sample t-test tests if the mean of a single quantitative variable is equal to some hypothesized population value. The figure illustrates the basic idea.
SPSS One Sample T-Test - Example
A scientist from Greenpeace believes that herrings in the North Sea don't grow as large as they used to. It's well known that - on average - herrings should weigh 400 grams. The scientist catches and weighs 40 herrings, resulting in herrings.sav. Can we conclude from these data that the average herring weighs less than 400 grams? We'll open the data by running the syntax below.
cd 'd:downloaded'. /*or wherever data file is located.
*2. Open data.
get file 'herrings.sav'.
1. Quick Data Check
Before we run any statistical tests, we always first want to have a basic idea of what the data look like. A fast way for doing so is taking a look at the histogram for body_weight. If we generate it by using FREQUENCIES, we'll get some helpful summary statistics in our chart as well.The required syntax is so simple that we won't bother about clicking through the menu here. We added /FORMAT NOTABLE to the command in order to suppress the actual frequency table; right now, we just want a histogram and some summary statistics.
frequencies body_weight
/format notable
/histogram.
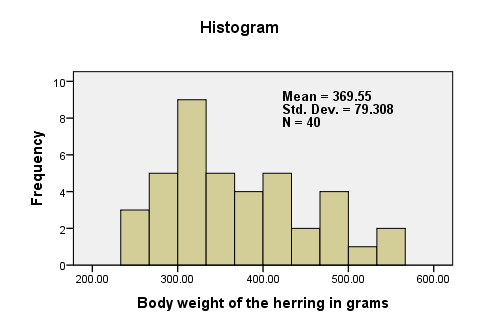
There are no very large or very small values for body_weight. The data thus look plausible. N = 40 means that the histogram is based on 40 cases (our entire sample). This tells us that there are no missing values. The mean weight is around 370 grams, which is 30 grams lower than the hypothesized 400 grams. The question is now: “if the average weight in the population is 400 grams, then what's the chance of finding a mean weight of only 370 grams in a sample of n = 40?”
2. Assumptions One Sample T-Test
Results from statistical procedures can only be taken seriously insofar as relevant assumptions are met. For a one-sample t-test, these are
- independent and identically distributed variables (or, less precisely, “independent observations”);
- normality: the test variable is normally distributed in the population;
Assumption 1 is beyond the scope of this tutorial. We assume it's been met by the data. The normality assumption not holding doesn't really affect the results for reasonable sample sizes (say, N > 30).
3. Run SPSS One-Sample T-Test
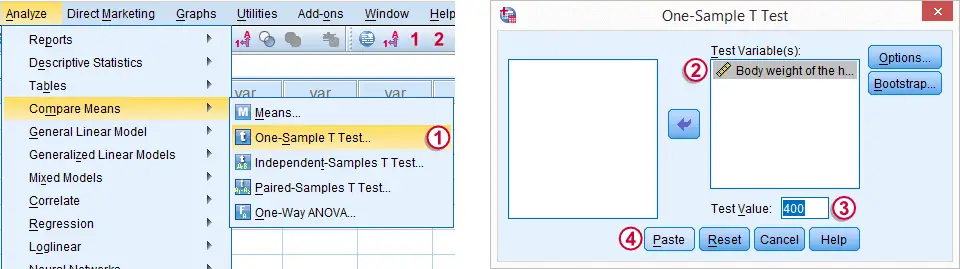
The screenshot walks you through running an SPSS one-sample t-test. Clicking results in the syntax below.
T-TEST
/TESTVAL=400
/MISSING=ANALYSIS
/VARIABLES=body_weight
/CRITERIA=CI(.95).
4. SPSS One-Sample T-Test Output

We'll first turn our attention to the One-Sample Statistics table. We already saw most of these statistics in our histogram but this table comes in a handier format for reporting these results.

The actual t-test results are found in the One-Sample Test table.
 -
-  The t value and its degrees of freedom (df) are not immediately interesting but we'll need them for reporting later on.
The t value and its degrees of freedom (df) are not immediately interesting but we'll need them for reporting later on.
 The p value, denoted by “Sig. (2-tailed)” is .02; if the population mean is exactly 400 grams, then there's only a 2% chance of finding the result we did. We usually reject the null hypothesis if p < .05. We thus conclude that herrings do not weight 400 grams (but probably less than that).
The p value, denoted by “Sig. (2-tailed)” is .02; if the population mean is exactly 400 grams, then there's only a 2% chance of finding the result we did. We usually reject the null hypothesis if p < .05. We thus conclude that herrings do not weight 400 grams (but probably less than that).
It's important to notice that the p value of .02 is 2-tailed. This means that the p value consists of a 1% chance for finding a difference < -30 grams and another 1% chance for finding a difference > 30 grams.
 The Mean Difference is simply the sample mean minus the hypothesized mean (369.55 - 400 = -30.45). We could have calculated it ourselves from previously discussed results.
The Mean Difference is simply the sample mean minus the hypothesized mean (369.55 - 400 = -30.45). We could have calculated it ourselves from previously discussed results.
5. Reporting a One-Sample T-Test
Regarding descriptive statistics, the very least we should report, is the mean, standard deviation and N on which these are based. Since these statistics don't say everything about the data, we personally like to include a histogram as well. We may report the t-test results by writing “we found that, on average, herrings weighed less than 400 grams; t(39) = -2.4, p = .020.”
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 14 COMMENTS:
By shahid Mughal on July 13th, 2015
very useful covering many features
By Linda Martell on July 15th, 2015
Good
By Junaid-ur-Rehman on January 2nd, 2016
Very helpful
By Shahid Mughal on May 26th, 2016
Very valuable procedure and interpretations
By Safia Brohi on June 21st, 2016
Very helpful , Good