Introduction & Practice Data File
Do you think running a two-way ANOVA with an interaction effect is challenging? Then this is the tutorial for you. We'll run the analysis by following a simple flowchart and we'll explain each step in simple language. After reading it, you'll know what to do and you'll understand why.
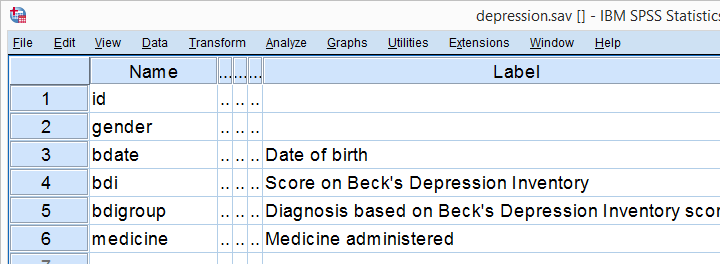
We'll use depression.sav throughout. The screenshot below shows it in variable view.
Research Questions
Very basically, 100 participants suffering from depression were divided into 4 groups of 25 each. Each group was given a different medicine. After 4 weeks, participants filled out the BDI, short for Beck's depression inventory. Our main research question is: did our different medicines result in different mean BDI scores? A secondary question is whether the BDI scores are related to gender in any way. In short we'll try to gain insight into 4 (medicines) x 2 (gender) = 8 mean BDI scores.
Quick Check: Histogram over Scores
Before jumping blindly into statistical tests, let's first see if our BDI scores make any sense in the first place. Before analyzing any metric variable, I always first inspect its histogram. The fastest way to create it is running the syntax below.
frequencies bdi
/format notable
/histogram.
Result
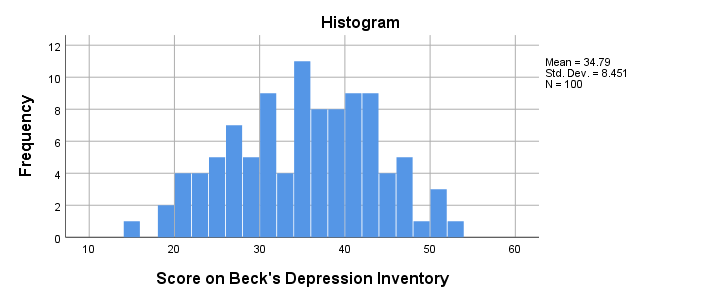
The scores look fine. We've perhaps one outlier who scores only 15 but we'll leave it in the data. The scores are roughly normally distributed and there's no need to specify any missing values.
ANOVA Assumptions
When we compare more than 2 means, we usually do so by ANOVA -short for analysis of variance. Doing so requires our data to meet the following assumptions:
- Independent observations (or independent and identically distributed variables). This often holds if each case contains a distinct person and the participants didn't interact.
- Homogeneity: the population variances are all equal over subpopulations. Violation of this assumption is less serious insofar as sample sizes are equal.
- Normality: the test variable must be normally distributed in each subpopulation. This assumption becomes less important insofar as the sample sizes are larger.
ANOVA Flowchart
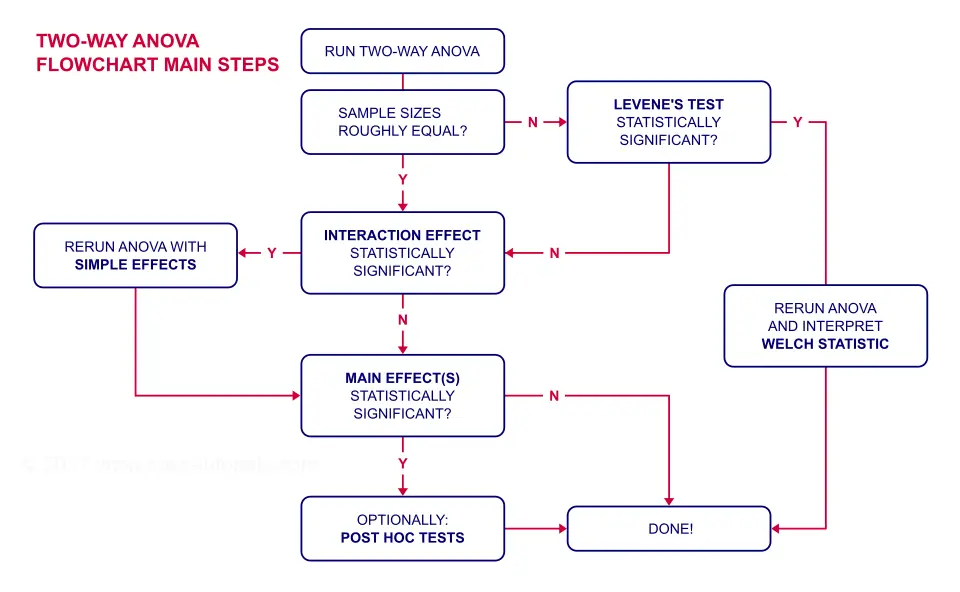
Inspecting Means and Sample Sizes
The first question in our ANOVA flowchart is whether the sample sizes are roughly equal. I like to run a means table for inspecting this because I'm going to need this table anyway for my report. I'll create it with the syntax below.
means bdi by gender by medicine
/cells count mean stddev.
*Note: MEANS allows you to choose exactly which statistics you want.
Result
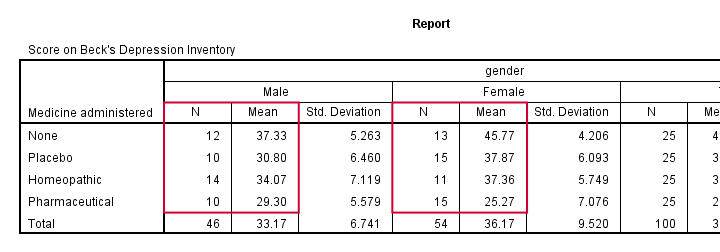
Note that this table shows the 8 means (2 genders * 4 medicines) that our analysis is all about. Each of these 8 means is based on 10 through 15 observations so the sample sizes are roughly equal.
This means that we don't need to bother about the homogeneity assumption. We can therefore skip Levene's test as shown in our flowchart.
Running Two-Way ANOVA in SPSS
We'll now run our two-way ANOVA through

 .
We'll then follow the screenshots below.
.
We'll then follow the screenshots below.
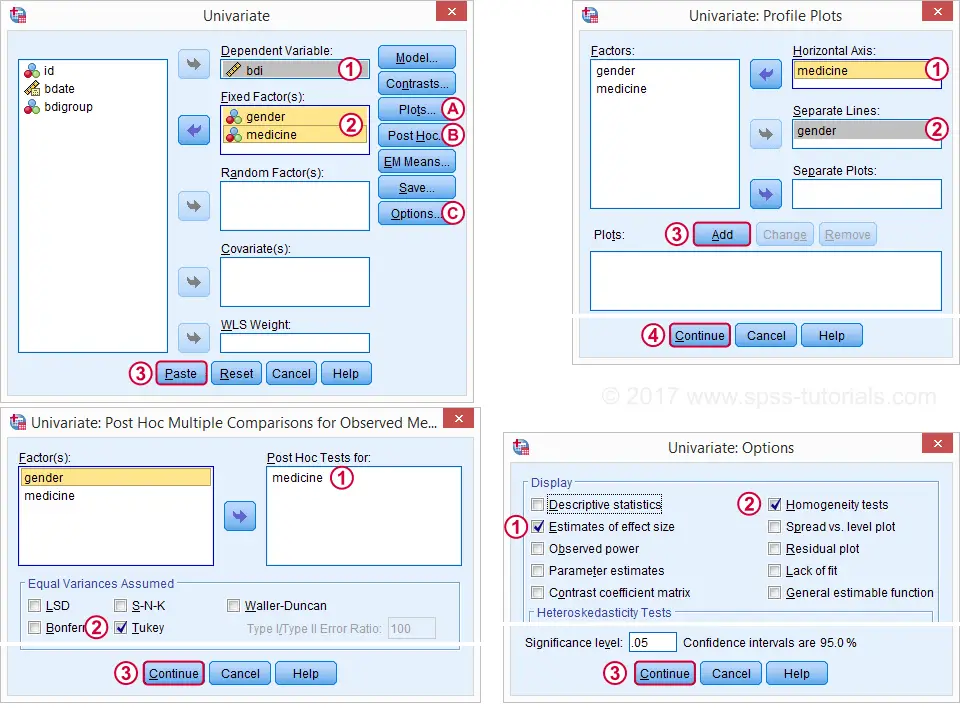
This results in the syntax below. Let's run it and see what happens.
UNIANOVA bdi BY gender medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PLOT=PROFILE(medicine*gender) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=gender medicine gender*medicine.
ANOVA Output - Between Subjects Effects
Following our flowchart, we should now find out if the interaction effect is statistically significant. A -somewhat arbitrary- convention is that an effect is statistically significant if “Sig.” < 0.05. According to the table below, our 2 main effects and our interaction are all statistically significant.
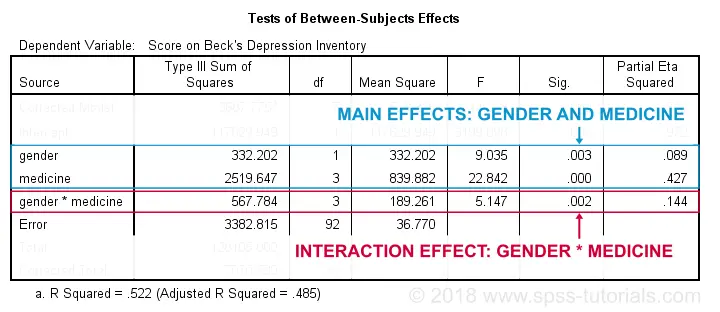
The flowchart says we should now rerun our ANOVA with simple effects. For now, we'll ignore the main effects -even if they're statistically significant. But why?! Well, this will become clear if we understand what our interaction effect really means. So let's inspect our profile plots.
ANOVA Output - Profile Plots
The profile plot shown below basically just shows the 8 means from our means table.If you ran the ANOVA like we just did, the “Estimated Marginal Means” are always the same as the observed means that we saw earlier. Interestingly, it also shows how medicine and gender affect these means.
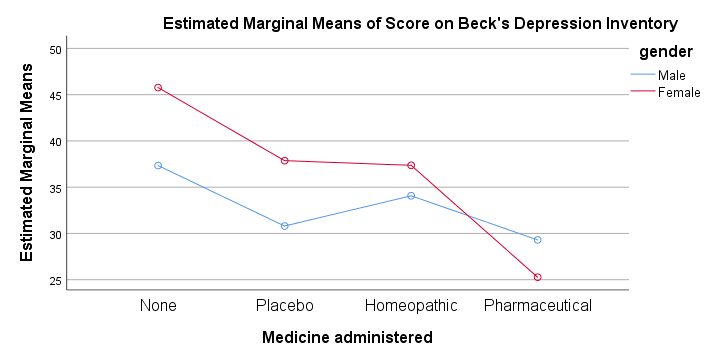
An interaction effect means that the effect of one factor depends on the other factor and it's shown by the lines in our profile plot not running parallel.
In this case, the effect for medicine interacts with gender. That is,
medicine affects females differently than males.
Roughly, we see the red line (females) descent quite steeply from “None” to “Pharmaceutical” whereas the blue line (males) is much more horizontal. Since it depends on gender,
there's no such thing as the effect of medicine.
So that's why we ignore the main effect of medicine -even if it's statistically significant. This main effect “lumps together” the different effects for males and females and this obscures -rather than clarifies- how medicine really affects the BDI scores.
Interaction Effect? Run Simple Effects.
So what should we do? Well, if medicine affects males and females differently, then we'll analyze male and female participants separately: we'll run a one-way ANOVA for just medicine on either group. This is what's meant by “simple effects” in our flowchart.
ANOVA with Simple Effects - Split File
How can we analyze 2 (or more) groups of cases separately? Well, SPSS has a terrific solution for this, known as SPLIT FILE. It requires that we first sort our cases so we'll do so as well.
sort cases by gender.
split file separate by gender.
Minor note: SPLIT FILE does not change your data in any way. It merely affects your output as we'll see in a minute. You can simply undo it by running
SPLIT FILE OFF.
but don't do so yet; we first want to run our one-way ANOVAs for inspecting our simple effects.
ANOVA with Simple Effects in SPSS
Since we switched on our SPLIT FILE, we can now just run one-way ANOVAs. We'll use

 .
The screenshots below guide you through the next steps.
.
The screenshots below guide you through the next steps.
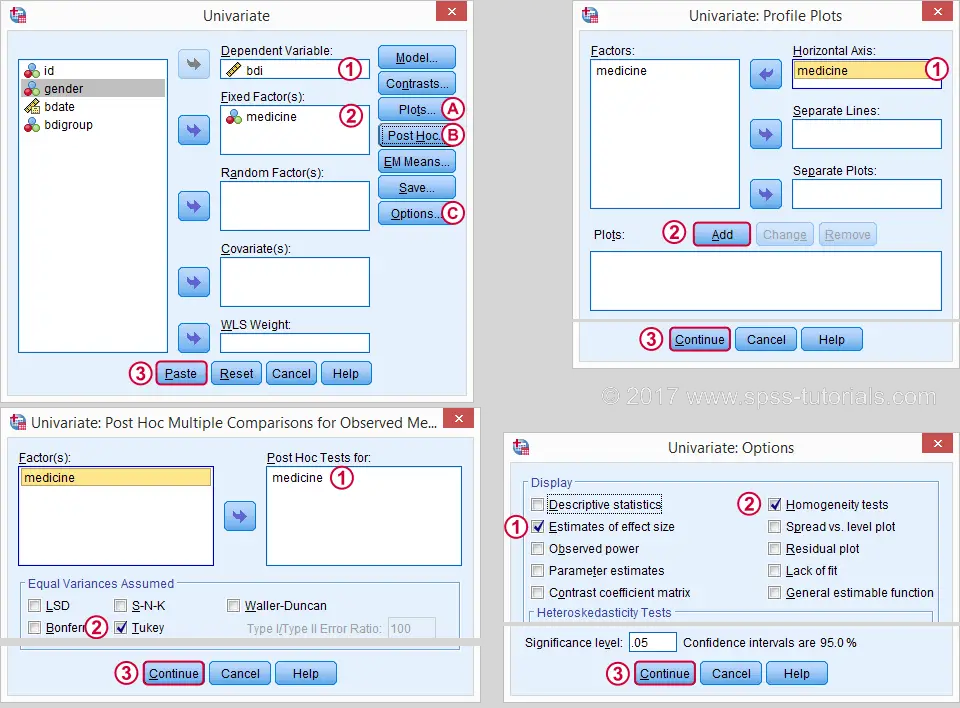
This results in the syntax below. Let's run it.
UNIANOVA bdi BY medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PLOT=PROFILE(medicine) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=medicine.
ANOVA Output - Between Subjects Effects
First off, note that the output window now contains all ANOVA results for male participants and then a similar set of results for females. According to our flowchart we should now inspect the main effect.
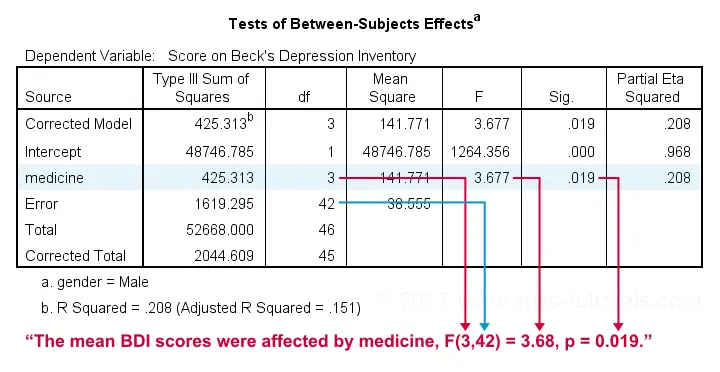
The effect for medicine is statistically significant. However, this just means it's probably not zero. But it's not very strong either as indicated by its partial eta squared of 0.208. This shouldn't come as a surprise. The 4 medicines don't differ much for males as we saw in our profile plots.
ANOVA Output - Post Hoc Tests
Our main effect suggests that our 4 medicines did not all perform similarly. But which one(s) really differ from which other one(s)? This question is addressed by our post hoc tests, in this case Tukey's HSD (“honestly significant differences”) comparisons.

This table compares each medicine with each other medicine (twice). The only comparison yielding p < 0.05 is “None” versus “Pharmaceutical”. Our profile plots show that these are the worst and best performing medicines for male participants. The means for all other medicines are too close to differ statistically significantly.
Female Participants
According to our flowchart, we're now done -at least for males. Interpreting the results for female participants is left as an exercise for the reader. However, I do want to point out the following:
- our profile plots show a much steeper line for females than for males.
- the main effect of medicine has a much higher partial eta squared of 0.63 for females.
- the effect of medicine has p = 0.000 for females and p = 0.019 for males.
- for females, all post hoc comparisons are statistically significant except for “Homeopathic” versus “Placebo” (p = 0.997).
All these findings indicate a much stronger effect of medicine for females than for males; there's a substantial interaction effect between medicine and gender on BDI scores. And this -again- is the reason why we need to analyze these groups separately and rerun our ANOVA with simple effects -like we just did.
Final Notes
Do you still think running a two-way ANOVA with an interaction effect is challenging? I hope this tutorial helped you understand the main line of thinking. And -hopefully!- things start to sink in for you -perhaps after a second reading.
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 51 COMMENTS:
By Lazarus Nweke on April 25th, 2023
ANOVA is useful in research work