SPSS TUTORIALS
- Z-Test - Assumptions
- SPSS Z-Tests Dialogs
- SPSS Z-Test Output
- SPSS Z-Tests - Strengths & Weaknesses
- APA Reporting Z-Tests
A z-test for independent proportions tests if 2 subpopulations
score similarly on a dichotomous variable.
Example: are the proportions (or percentages) of correct answers equal between male and female students?
Although z-tests are widely used in the social sciences, they were only introduced in SPSS version 27. So let's see how to run them and interpret their output. We'll use exam-questions.sav -partly shown below- throughout this tutorial.
Now, before running the actual z-tests, we first need to make sure we meet their assumptions.
Z-Test - Assumptions
Z-tests for independent proportions require 2 assumptions:
- independent observations and
- sufficient sample sizes.
Regarding this second assumption, Agresti and Franklin (2014)2 propose that both outcomes should occur at least 10 times in both samples. That is,
$$p_a n_a \ge 10, (1 - p_a) n_a \ge 10, p_b n_b \ge 10, (1 - p_b) n_b \ge 10$$
where
- \(n_a\) and \(n_b\) denote the sample sizes of groups a and b and
- \(p_a\) and \(p_b\) denote the proportions of “successes” in both groups.
Note that some other textbooks3,4 suggest that smaller sample sizes may be sufficient. If you're not sure about meeting the sample sizes assumption, run a minimal CROSSTABS command as in crosstabs v1 to v5 by sex. As shown below, note that all 5 exam questions easily meet the sample sizes assumption.
For insufficient sample sizes, Agresti and Caffo (2000)1 proposed a simple adjustment for computing confidence intervals: simply add one observation for each outcome to each group (4 observations in total) and proceed as usual with these adjusted sample sizes.
SPSS Z-Tests Dialogs
First off, let's navigate to
and fill out the dialogs as shown below.
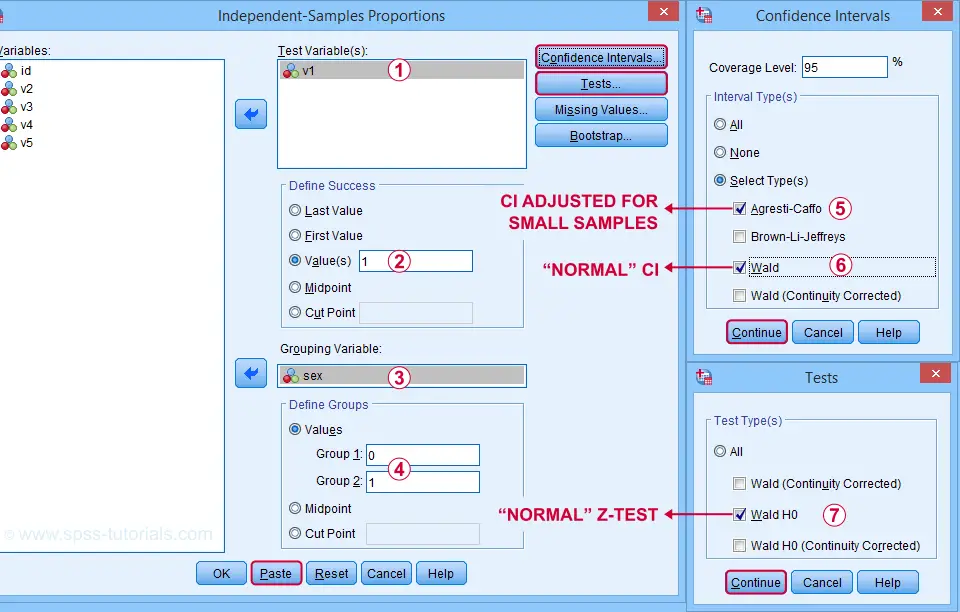
Clicking “Paste” results in the SPSS syntax below. Let's run it.
PROPORTIONS
/INDEPENDENTSAMPLES v1 BY sex SELECT=LEVEL(0 ,1 ) CITYPES=AGRESTI_CAFFO WALD TESTTYPES=WALDH0
/SUCCESS VALUE=LEVEL(1 )
/CRITERIA CILEVEL=95
/MISSING SCOPE=ANALYSIS USERMISSING=EXCLUDE.
SPSS Z-Test Output
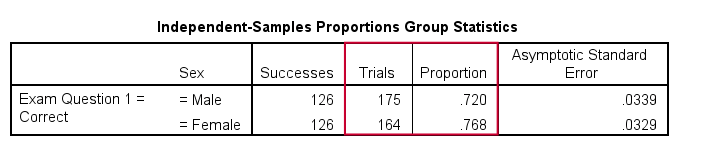
The first table shows the observed proportions for male and female students. Note that female students seem to perform somewhat better: a proportion of .768 (or 76.8%) answered correctly as compared to .720 for male students.
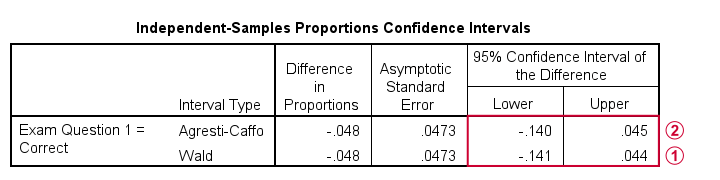
The second output table shows that the difference between our sample proportions is -.048.
The “normal” 95% confidence interval for this difference (denoted as Wald) is [-.141, .044]. Note that this CI encloses zero: male and female populations performing equally well is within the range of likely values.
I don't recommend reporting the Agresti-Caffo corrected CI unless your data don't meet the sample sizes assumption.
The third table shows the z-test results. First note that 
p(2-tailed) = .309. As a rule of thumb, we
reject the null hypothesis if p < 0.05
which is not the case here. Conclusion: we do not reject the null hypothesis that the population difference is zero. That is: the sample difference of -.048 is not statistically significant.
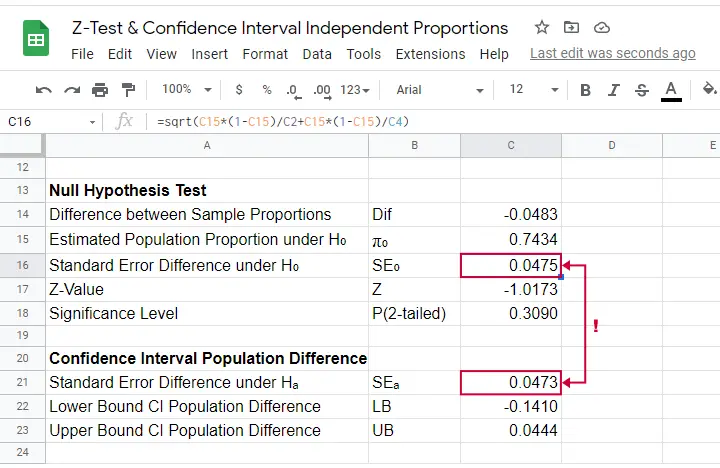
Finally, note that SPSS reports 
the wrong standard error for this test. The correct standard error is 0.0475 as computed in this Googlesheet (read-only) shown below.
SPSS Z-Tests - Strengths and Weaknesses
What's good about z-tests in SPSS is that
- you can analyze many dependent variables in one go;
- both the independent and dependent variables may be either string variables or numeric variables;We also tested SPSS z-tests on a mixture of string and numeric dependent variables. Although doing so is very awkward, the results were correct.
- many corrections -such as Agresti-Caffo- are available.
However, what I really don't like about SPSS z-tests is that
- no warning is issued if the sample sizes assumption isn't met;
- no effect size measures are available. Cohen’s H seems completely absent from SPSS and phi coefficients are available from CROSSTABS or CORRELATIONS;
- SPSS reports the wrong standard error for the actual z-test;
- z-tests and confidence intervals are reported in separate tables. I'd rather see these as different columns in a single table with one row per dependent variable.
APA Reporting Z-Tests
The APA guidelines don't explicitly mention how to report z-tests. However, it makes sense to report something like
the difference between males and females
was not significant, z = -1.02, p(2-tailed) = .309.
You should obviously report the actual proportions and sample sizes as well. If you analyzed multiple dependent variables, you may want to create a table showing
- both proportions being compared;
- the difference between the proportions and its confidence interval;
- z and p(2-tailed) for the null hypothesis of equal population proportions;
- some effect size measure.
References
- Agresti, A & Caffo, B. (2000). Simple and Effective Confidence Intervals for Proportions and Differences of Proportions. The American Statistician, 54(4), 280-288.
- Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
- Twisk, J.W.R. (2016). Inleiding in de Toegepaste Biostatistiek [Introduction to Applied Biostatistics]. Houten: Bohn Stafleu van Loghum.
- Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [Statistics, part 3]. Amsterdam: Boom.
THIS TUTORIAL HAS 5 COMMENTS:
By Jon Peck on March 9th, 2022
The std error is not wrong.
SPSS is showing ASE1 or the ASE under the alternative hypothesis (C21 in the spreadsheet), but ASE0 is used in calculating the Z statistic. This is what’s done in all the similar statistics in CROSSTABS.
By Ruben Geert van den Berg on March 10th, 2022
Yes, I already figured that out.
But why would you report the SE for the CI instead of the SE for the p-value when reporting the p-value?
Statistics lesson 1 is pretty much that Z = Dif/SE but this does not hold for the SPSS output for the p-value.
I can't help finding that odd.
Precisely which textbooks advocate this practice?
By Jon Peck on March 10th, 2022
An SPSS statistician says,
"A primary reason for creating a whole new procedure with many different options for tests and confidence intervals was that inferences on proportions are just not that simple, even with a single proportion. Three of the five tests for independent samples involve continuity corrections, so d/SE doesn’t get you Z regardless of what you put for the SE. Similar considerations hold for the other types of analyses (single and paired). Consistency with CROSSTABS was another nontrivial consideration."
By Ruben Geert van den Berg on March 11th, 2022
I think a software manufacturer should simply implement well-established procedures. Not contest them.
IMHO, a "standard" (uncorrected) z-test is well-established because the main text books (such as Agresti/Franklin) all agree on its formulas.
So if you -for whatever reason- deviate from precisely these formulas, then the general consensus will be that your results are wrong. Also note that I didn't mention any of the continuity-corrected variations in my tutorial.
Now, it's fine to argue that well-established procedures are not optimal. You're probably right. But in this case, you should propose alternatives for them with different names and try to get those into the standard literature -just like the Agresti-Caffo CI's.
But simply deviating from the formulas is like disobeying the law because you don't agree with it.
P.s. precisely which CROSSTABS statistics does the statistician refer to? I know there's the BPROP subcommand but it doesn't explicitly report exact p-values/SE's...
By Jon Peck on March 11th, 2022
The procedure implements well-established measures, including the older ones that may or may not perform well, and the ones that have been established in the literature as alternatives.
The algorithms show that all of what’s in there is based on standard literature. All of the measures are also included in SAS.
The issue of how to present them is arguable, but there’s no optimal solution. In CROSSTABS there are over a dozen measures presented in this way, though with footnotes clarifying what the SEs are, which will be added to PROPORTIONS. While in the CROSSTABS case all the test statistics involved use an ASE0, in some cases in PROPORTIONS it’s not that simple.