SPSS Shapiro-Wilk Test – Quick Tutorial with Example

• Shapiro-Wilk Test - What is It?
• Shapiro-Wilk Test - Null Hypothesis
• Running the Shapiro-Wilk Test in SPSS
• Shapiro-Wilk Test - Interpretation
• Reporting a Shapiro-Wilk Test in APA style

Shapiro-Wilk Test - What is It?

The Shapiro-Wilk test examines if a variable
is normally distributed in some population. Like so, the Shapiro-Wilk serves the exact same purpose as the Kolmogorov-Smirnov test. Some statisticians claim the latter is worse due to its lower statistical power. Others disagree.

As an example of a Shapiro-Wilk test, let's say a scientist claims that the reaction times of all people -a population- on some task are normally distributed. He draws a random sample of N = 233 people and measures their reaction times. A histogram of the results is shown below.

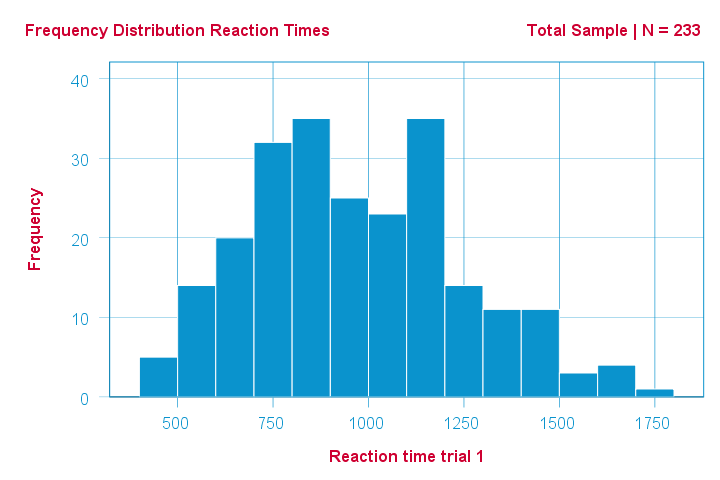
This frequency distribution seems somewhat bimodal. Other than that, it looks reasonably -but not exactly- normal. However, sample outcomes usually differ from their population counterparts. The big question is: how likely is the observed distribution if the reaction times
are exactly normally distributed in the entire population? The Shapiro-Wilk test answers precisely that.

How Does the Shapiro-Wilk Test Work?

A technically correct explanation is given on this Wikipedia page. However, a simpler -but not technically correct- explanation is this: the Shapiro-Wilk test first quantifies the similarity between the observed and normal distributions as a single number: it superimposes a normal curve over the observed distribution as shown below. It then computes which percentage of our sample overlaps with it: a similarity percentage.

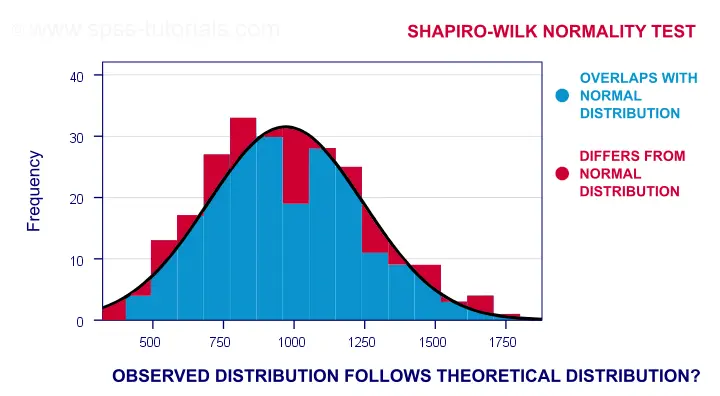
Finally, the Shapiro-Wilk test computes the probability of finding this observed -or a smaller- similarity percentage. It does so under the assumption that the population distribution is exactly normal: the null hypothesis.

Shapiro-Wilk Test - Null Hypothesis

The null hypothesis for the Shapiro-Wilk test is that a variable is normally distributed in some population. A different way to say the same is that a variable’s values are a simple random sample from a normal distribution. As a rule of thumb, we reject the null hypothesis if p < 0.05. So in this case we conclude that our variable is not normally distributed.
Why? Well, p is basically the probability of finding our data if the null hypothesis is true. If this probability is (very) small -but we found our data anyway- then the null hypothesis was probably wrong.

Shapiro-Wilk Test - SPSS Example Data

A sample of N = 236 people completed a number of speedtasks. Their reaction times are in speedtasks.sav, partly shown below. We'll only use the first five trials in variables r01 through r05.

I recommend you always thoroughly inspect all variables you'd like to analyze. Since our reaction times in milliseconds are quantitative variables, we'll run some quick histograms over them. I prefer doing so from the short syntax below. Easier -but slower- methods are covered in Creating Histograms in SPSS.

Results

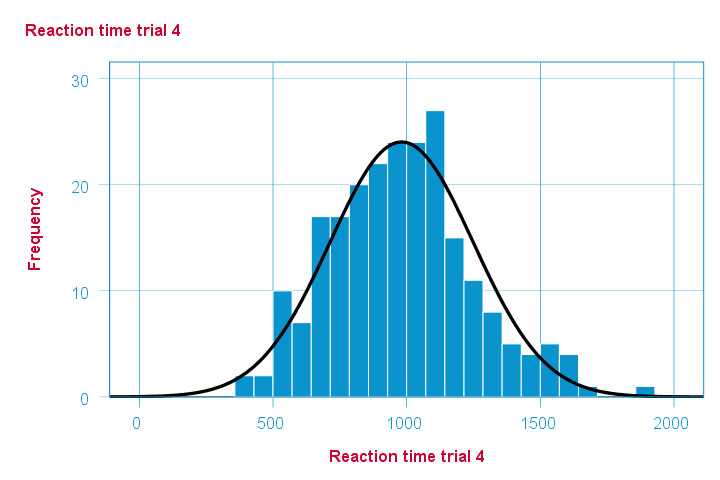
Note that some of the 5 histograms look messed up. Some data seem corrupted and had better not be seriously analyzed. An exception is trial 4 (shown below) which looks plausible -even reasonably normally distributed.

Descriptive Statistics - Skewness & Kurtosis

If you're reading this to complete some assignment, you're probably asked to report some descriptive statistics for some variables. These often include the median, standard deviation, skewness and kurtosis. Why? Well, for a normal distribution,

• skewness = 0: it's absolutely symmetrical and
• kurtosis = 0 too: it's neither peaked (“leptokurtic”) nor flattened (“platykurtic”).

So if we sample many values from such a distribution, the resulting variable should have both skewness and kurtosis close to zero. You can get such statistics from FREQUENCIES but I prefer using MEANS: it results in the best table format and its syntax is short and simple.

Results

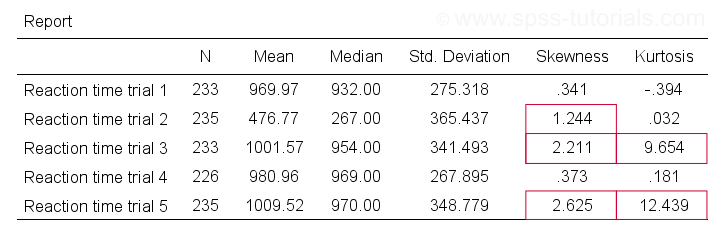
Trials 2, 3 and 5 all have a huge skewness and/or kurtosis. This suggests that they are not normally distributed in the entire population. Skewness and kurtosis are closer to zero for trials 1 and 4.
So now that we've a basic idea what our data look like, let's proceed with the actual test.

Running the Shapiro-Wilk Test in SPSS

The screenshots below guide you through running a Shapiro-Wilk test correctly in SPSS. We'll add the resulting syntax as well.

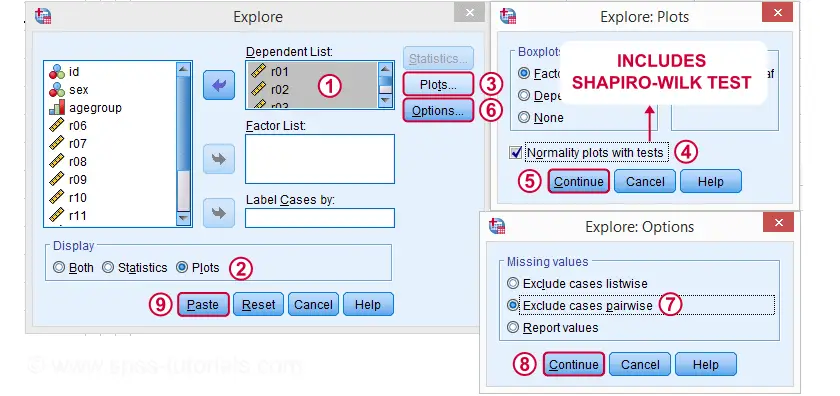
Following these screenshots results in the syntax below.

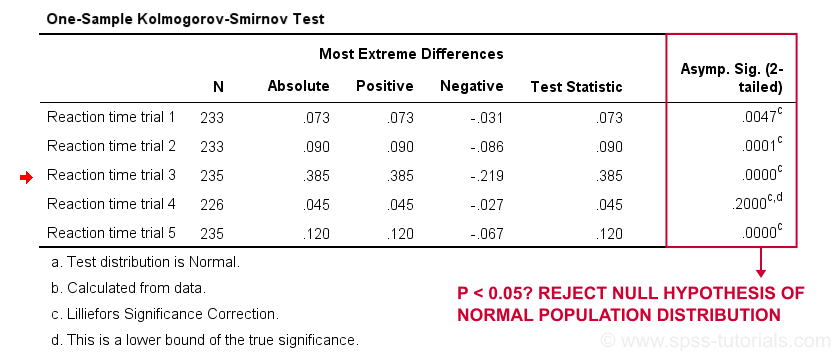
Running this syntax creates a bunch of output. However, the one table we're looking for -“Tests of Normality”- is shown below.

Shapiro-Wilk Test - Interpretation

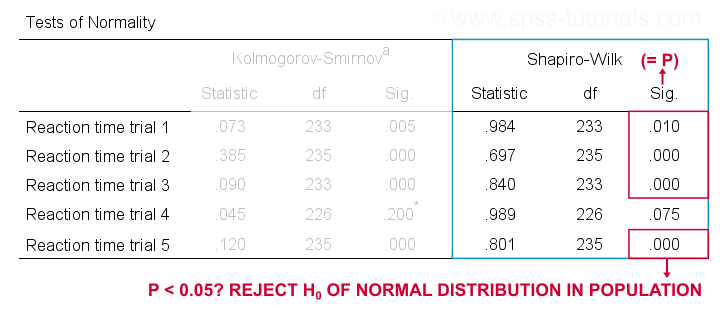
We reject the null hypotheses of normal population distributions
for trials 1, 2, 3 and 5 at α = 0.05. “Sig.” or p is the probability of finding the observed -or a larger- deviation from normality in our sample if the distribution is exactly normal in our population. If trial 1 is normally distributed in the population, there's a mere 0.01 -or 1%- chance of finding these sample data. These values are unlikely to have been sampled from a normal distribution. So the population distribution probably wasn't normal after all.

We therefore reject this null hypothesis. Conclusion: trials 1, 2, 3 and 5 are probably not normally distributed in the population.

The only exception is trial 4: if this variable is normally distributed in the population, there's a 0.075 -or 7.5%- chance of finding the nonnormality observed in our data. That is, there's a reasonable chance that this nonnormality is solely due to sampling error. So for trial 4, we retain the null hypothesis
of population normality because p > 0.05. We can't tell for sure if the population distribution is normal. But given these data, we'll believe it. For now anyway.

Reporting a Shapiro-Wilk Test in APA style

For reporting a Shapiro-Wilk test in APA style, we include 3 numbers:

• the test statistic W -mislabeled “Statistic” in SPSS;
• its associated df -short for degrees of freedom and
• its significance level p -labeled “Sig.” in SPSS.

The screenshot shows how to put these numbers together for trial 1.

Limited Usefulness of Normality Tests

The Shapiro-Wilk and Kolmogorov-Smirnov test both examine if a variable is normally distributed in some population. But why even bother? Well, that's because many statistical tests -including ANOVA, t-tests and regression- require the normality assumption: variables must be normally distributed in the population. However, the normality assumption is only needed for small sample sizes of -say- N ≤ 20 or so. For larger sample sizes, the sampling distribution of the mean is always normal, regardless how values are distributed in the population. This phenomenon is known as the central limit theorem. And the consequence is that many test results are unaffected by even severe violations of normality.
So if sample sizes are reasonable, normality tests are often pointless. Sadly, few statistics instructors seem to be aware of this and still bother students with such tests. And that's why I wrote this tutorial anyway.

Hey! But what if sample sizes are small, say N < 20 or so? Well, in that case, many tests do require normally distributed variables. However, normality tests typically have low power in small sample sizes. As a consequence, even substantial deviations from normality may not be statistically significant. So when you really need normality, normality tests are unlikely to detect that it's actually violated. Which renders them pretty useless.

Thanks for reading.

SPSS Kolmogorov-Smirnov Test for Normality

An alternative normality test is the Shapiro-Wilk test.

• What is a Kolmogorov-Smirnov normality test?
• SPSS Kolmogorov-Smirnov test from NPAR TESTS
• SPSS Kolmogorov-Smirnov test from EXAMINE VARIABLES
• Reporting a Kolmogorov-Smirnov Test
• Wrong Results in SPSS?

What is a Kolmogorov-Smirnov normality test?

The Kolmogorov-Smirnov test examines if scores
are likely to follow some distribution in some population. For avoiding confusion, there's 2 Kolmogorov-Smirnov tests:

• there's the one sample Kolmogorov-Smirnov test for testing if a variable follows a given distribution in a population. This “given distribution” is usually -not always- the normal distribution, hence “Kolmogorov-Smirnov normality test”.
• there's also the (much less common) independent samples Kolmogorov-Smirnov test for testing if a variable has identical distributions in 2 populations.

In theory, “Kolmogorov-Smirnov test” could refer to either test (but usually refers to the one-sample Kolmogorov-Smirnov test) and had better be avoided. By the way, both Kolmogorov-Smirnov tests are present in SPSS.

Kolmogorov-Smirnov Test - Simple Example

So say I've a population of 1,000,000 people. I think their reaction times on some task are perfectly normally distributed. I sample 233 of these people and measure their reaction times.
Now the observed frequency distribution of these will probably differ a bit -but not too much- from a normal distribution. So I run a histogram over observed reaction times and superimpose a normal distribution with the same mean and standard deviation. The result is shown below.

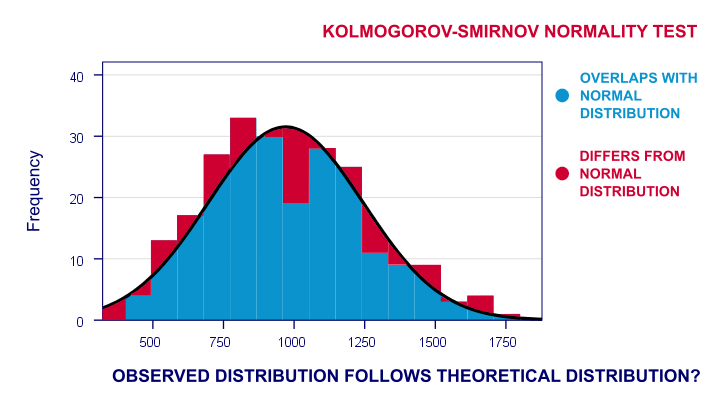
The frequency distribution of my scores doesn't entirely overlap with my normal curve. Now, I could calculate the percentage of cases that deviate from the normal curve -the percentage of red areas in the chart. This percentage is a test statistic: it expresses in a single number how much my data differ from my null hypothesis. So it indicates to what extent the observed scores deviate from a normal distribution.
Now, if my null hypothesis is true, then this deviation percentage should probably be quite small. That is, a small deviation has a high probability value or p-value.
Reversely, a huge deviation percentage is very unlikely and suggests that my reaction times don't follow a normal distribution in the entire population. So a large deviation has a low p-value. As a rule of thumb, we reject the null hypothesis if p < 0.05. So if p < 0.05, we don't believe that our variable follows a normal distribution in our population.

Kolmogorov-Smirnov Test - Test Statistic

So that's the easiest way to understand how the Kolmogorov-Smirnov normality test works. Computationally, however, it works differently: it compares the observed versus the expected cumulative relative frequencies as shown below.

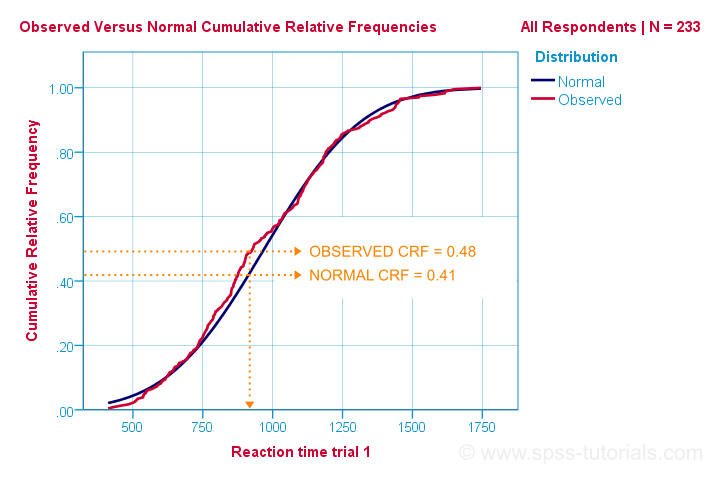
The Kolmogorov-Smirnov test uses the maximal absolute difference between these curves as its test statistic denoted by D. In this chart, the maximal absolute difference D is (0.48 - 0.41 =) 0.07 and it occurs at a reaction time of 960 milliseconds. Keep in mind that D = 0.07 as we'll encounter it in our SPSS output in a minute.

The Kolmogorov-Smirnov test in SPSS

There's 2 ways to run the test in SPSS:

• NPAR TESTS as found under Analyze Nonparametric Tests Legacy Dialogs 1-Sample K-S... is our method of choice because it creates nicely detailed output.
• EXAMINE VARIABLES from Analyze Descriptive Statistics Explore is an alternative. This command runs both the Kolmogorov-Smirnov test and the Shapiro-Wilk normality test.
  Note that EXAMINE VARIABLES uses listwise exclusion of missing values by default. So if I test 5 variables, my 5 tests only use cases which don't have any missings on any of these 5 variables. This is usually not what you want but we'll show how to avoid this.

We'll demonstrate both methods using speedtasks.sav throughout, part of which is shown below.

Our main research question is which of the reaction time variables is likely
to be normally distributed in our population? These data are a textbook example of why you should thoroughly inspect your data before you start editing or analyzing them. Let's do just that and run some histograms from the syntax below.

Result

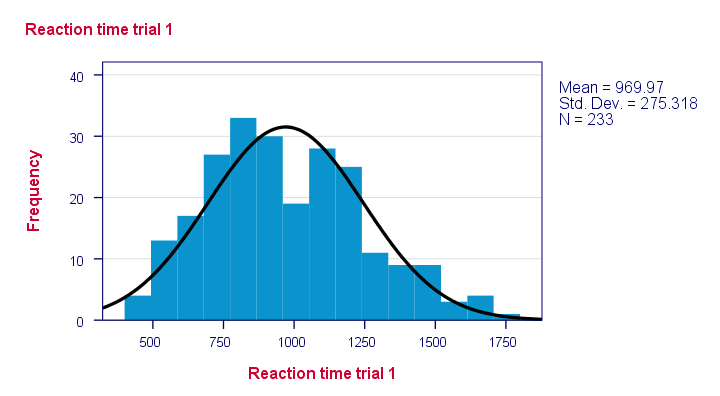
Note that some distributions do not look plausible at all. But which ones are likely to be normally distributed?

SPSS Kolmogorov-Smirnov test from NPAR TESTS

Our preferred option for running the Kolmogorov-Smirnov test is under Analyze Nonparametric Tests Legacy Dialogs 1-Sample K-S... as shown below.

Next, we just fill out the dialog as shown below.

Clicking Paste results in the syntax below. Let's run it.

Kolmogorov-Smirnov Test Syntax from Nonparametric Tests

Results

First off, note that the test statistic for our first variable is 0.073 -just like we saw in our cumulative relative frequencies chart a bit earlier on. The chart holds the exact same data we just ran our test on so these results nicely converge.
Regarding our research question: only the reaction times for trial 4 seem to be normally distributed.

SPSS Kolmogorov-Smirnov test from EXAMINE VARIABLES

An alternative way to run the Kolmogorov-Smirnov test starts from Analyze Descriptive Statistics Explore as shown below.

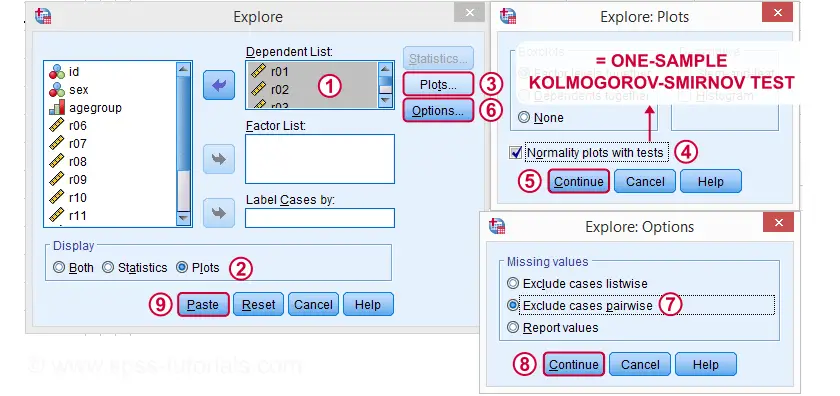
Kolmogorov-Smirnov Test Syntax from Nonparametric Tests

Results

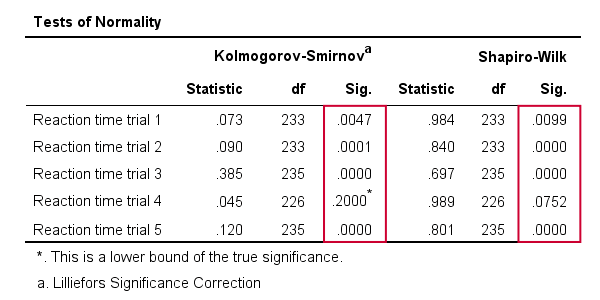
As a rule of thumb, we conclude that a variable is not normally distributed if “Sig.” < 0.05. So both the Kolmogorov-Smirnov test as well as the Shapiro-Wilk test results suggest that only Reaction time trial 4 follows a normal distribution in the entire population.
Further, note that the Kolmogorov-Smirnov test results are identical to those obtained from NPAR TESTS.

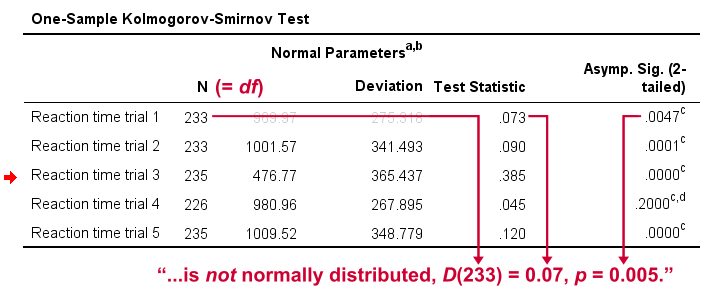
Reporting a Kolmogorov-Smirnov Test

For reporting our test results following APA guidelines, we'll write something like “a Kolmogorov-Smirnov test indicates that the reaction times on trial 1 do not follow a normal distribution, D(233) = 0.07, p = 0.005.” For additional variables, try and shorten this but make sure you include

• D (for “difference”), the Kolmogorov-Smirnov test statistic,
• df, the degrees of freedom (which is equal to N) and
• p, the statistical significance.

Wrong Results in SPSS?

If you're a student who just wants to pass a test, you can stop reading now. Just follow the steps we discussed so far and you'll be good.

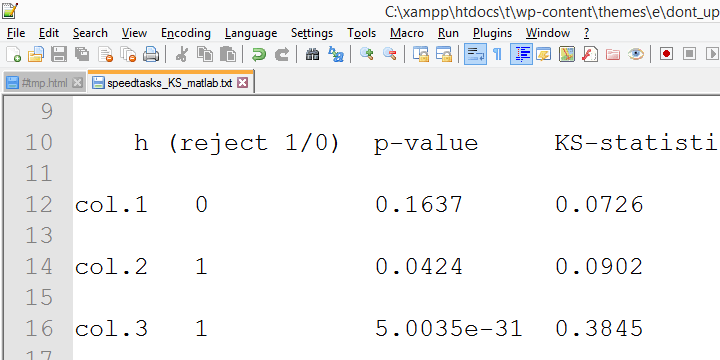
Right, now let's run the exact same tests again in SPSS version 18 and take a look at the output.

In this output, the exact p-values are included and -fortunately- they are very close to the asymptotic p-values. Less fortunately, though, the SPSS version 18 results are wildly different
from the SPSS version 24 results we reported thus far.
The reason seems to be the Lilliefors significance correction which is applied in newer SPSS versions. The result seems to be that the asymptotic significance levels differ much more from the exact significance than they did when the correction is not implied. This raises serious doubts regarding the correctness of the “Lilliefors results” -the default in newer SPSS versions.
Converging evidence for this suggestion was gathered by my colleague Alwin Stegeman who reran all tests in Matlab. The Matlab results agree with the SPSS 18 results and -hence- not with the newer results.

Kolmogorov-Smirnov normality test - Limited Usefulness

The Kolmogorov-Smirnov test is often to test the normality assumption required by many statistical tests such as ANOVA, the t-test and many others. However, it is almost routinely overlooked that such tests are robust against a violation of this assumption if sample sizes are reasonable, say N ≥ 25.The underlying reason for this is the central limit theorem. Therefore, normality tests are only needed for small sample sizes if the aim is to satisfy the normality assumption.
Unfortunately, small sample sizes result in low statistical power for normality tests. This means that substantial deviations from normality will not result in statistical significance. The test says there's no deviation from normality while it's actually huge. In short, the situation in which normality tests are needed -small sample sizes- is also the situation in which they perform poorly.

Thanks for reading.