SPSS Stepwise Regression – Simple Tutorial
A magazine wants to improve their customer satisfaction. They surveyed some readers on  their overall satisfaction as well as
their overall satisfaction as well as
 satisfaction with some quality aspects. Their basic question is
“which aspects have most impact on customer satisfaction?”
We'll try to answer this question with regression analysis. Overall satisfaction is our dependent variable (or criterion) and the quality aspects are our independent variables (or predictors).
satisfaction with some quality aspects. Their basic question is
“which aspects have most impact on customer satisfaction?”
We'll try to answer this question with regression analysis. Overall satisfaction is our dependent variable (or criterion) and the quality aspects are our independent variables (or predictors).
These data -downloadable from magazine_reg.sav- have already been inspected and prepared in Stepwise Regression in SPSS - Data Preparation.
Preliminary Settings
Our data contain a FILTER variable which we'll switch on with the syntax below. We also want to see both variable names and labels in our output so we'll set that as well.
filter by filt1.
*2. Show variable names and labels in output.
set tvars both.
SPSS ENTER Regression
We'll first run a default linear regression on our data as shown by the screenshots below.
Let's now fill in the dialog and subdialogs as shown below.
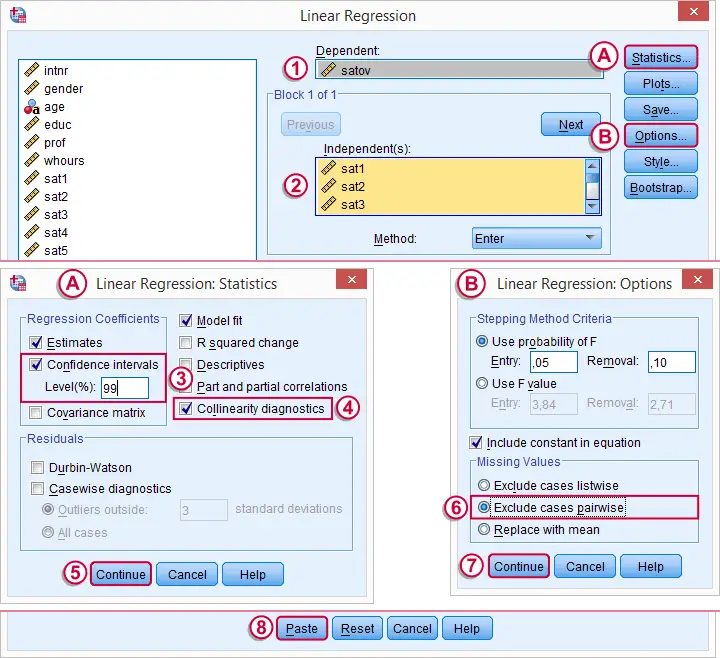
Note that we usually select  because it uses as many cases as possible for computing the correlations on which our regression is based.
because it uses as many cases as possible for computing the correlations on which our regression is based.
Clicking results in the syntax below. We'll run it right away.
SPSS ENTER Regression - Syntax
REGRESSION
/MISSING PAIRWISE
/STATISTICS COEFF CI(99) OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT satov
/METHOD=ENTER sat1 sat2 sat3 sat4 sat5 sat6 sat7 sat8 sat9.
SPSS ENTER Regression - Output
In our output, we first inspect our coefficients table as shown below.
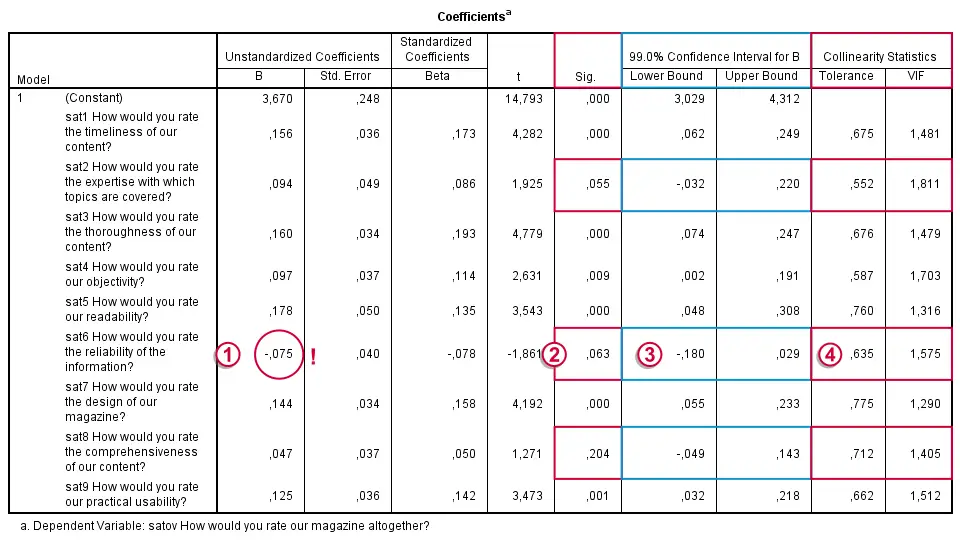
Some things are going dreadfully wrong here:
 The b-coefficient of -0.075 suggests that lower “reliability of information” is associated with higher satisfaction. However, these variables have a positive correlation (r = 0.28 with a p-value of 0.000).
The b-coefficient of -0.075 suggests that lower “reliability of information” is associated with higher satisfaction. However, these variables have a positive correlation (r = 0.28 with a p-value of 0.000).
 This weird b-coefficient is not statistically significant: there's a 0.063 probability of finding this coefficient in our sample if it's zero in the population. This goes for some other predictors as well.
This weird b-coefficient is not statistically significant: there's a 0.063 probability of finding this coefficient in our sample if it's zero in the population. This goes for some other predictors as well.
This problem is known as multicollinearity: we entered too many intercorrelated predictors into our regression model. The (limited) r square gets smeared out over 9 predictors here. Therefore, the unique contributions of some predictors become so small that they can no longer be distinguished from zero.
 The confidence intervals confirm this: it includes zero for three b-coefficients.
The confidence intervals confirm this: it includes zero for three b-coefficients.
 A rule of thumb is that Tolerance < 0.10 indicates multicollinearity. In our case, the Tolerance statistic fails dramatically in detecting multicollinearity which is clearly present. Our experience is that this is usually the case.
A rule of thumb is that Tolerance < 0.10 indicates multicollinearity. In our case, the Tolerance statistic fails dramatically in detecting multicollinearity which is clearly present. Our experience is that this is usually the case.
Resolving Multicollinearity with Stepwise Regression
A method that almost always resolves multicollinearity is stepwise regression. We specify which predictors we'd like to include. SPSS then inspects which of these predictors really contribute to predicting our dependent variable and excludes those who don't.
Like so, we usually end up with fewer predictors than we specify. However, those that remain tend to have solid, significant b-coefficients in the expected direction: higher scores on quality aspects are associated with higher scores on satisfaction. So let's do it.
SPSS Stepwise Regression - Syntax
We copy-paste our previous syntax and set METHOD=STEPWISE in the last line. Like so, we end up with the syntax below. We'll run it and explain the main results.
REGRESSION
/MISSING PAIRWISE
/STATISTICS COEFF OUTS CI(99) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT satov
/METHOD=stepwise sat1 sat2 sat3 sat4 sat5 sat6 sat7 sat8 sat9.
SPSS Stepwise Regression - Variables Entered

This table illustrates the stepwise method: SPSS starts with zero predictors and then adds the strongest predictor, sat1, to the model if its b-coefficient in statistically significant (p < 0.05, see last column).
It then adds the second strongest predictor (sat3). Because doing so may render previously entered predictors not significant, SPSS may remove some of them -which doesn't happen in this example.
This process continues until none of the excluded predictors contributes significantly to the included predictors. In our example, 6 out of 9 predictors are entered and none of those are removed.
SPSS Stepwise Regression - Model Summary

SPSS built a model in 6 steps, each of which adds a predictor to the equation. While more predictors are added, adjusted r-square levels off: adding a second predictor to the first raises it with 0.087, but adding a sixth predictor to the previous 5 only results in a 0.012 point increase. There's no point in adding more than 6 predictors.
Our final adjusted r-square is 0.39, which means that our 6 predictors account for 39% of the variance in overall satisfaction. This is somewhat disappointing but pretty normal in social science research.
SPSS Stepwise Regression - Coefficients
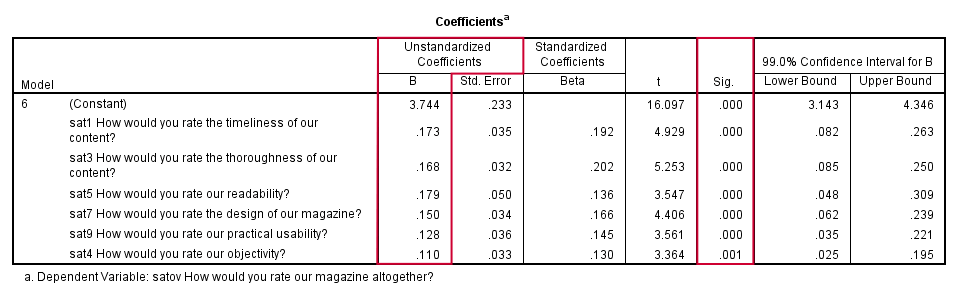
In our coefficients table, we only look at our sixth and final model. Like we predicted, our b-coefficients are all significant and in logical directions. Because all predictors have identical (Likert) scales, we prefer interpreting the b-coefficients rather than the beta coefficients. Our final model states that
satov’ = 3.744 + 0.173 sat1 + 0.168 sat3 + 0.179 sat5
+ 0.150 sat7 + 0.128 sat9 + 0.110 sat4
Our strongest predictor is sat5 (readability): a 1 point increase is associated with a 0.179 point increase in satov (overall satisfaction). Our model doesn't prove that this relation is causal but it seems reasonable that improving readability will cause slightly higher overall satisfaction with our magazine.
SPSS – Data Preparation for Regression
A magazine publisher surveyed their readers on
 their overall satisfaction with some magazine and
their overall satisfaction with some magazine and
 a number of quality aspects.
a number of quality aspects.
The data -part of which is shown below- are in magazine.sav.

The main research question is which quality aspects have most impact on overall satisfaction? Now, when working with real world data, the first thing you want to do are some basic data checks. This tutorial walks you through just those. The actual regression analysis on the prepared data is covered in the next tutorial, Stepwise Regression in SPSS - Example.
Check for User Missing Values and Coding
We'll first check if we need to set any user missing values. A solid approach here is to run frequency tables while showing values as well as value labels.
set tnumbers both tvars both.
*Check frequency tables for user missing values.
frequencies satov to sat9.
Result

Set User Missing Values
We learn two things from our frequency tables. First, all variables are positively coded: higher values correspond to more positive attitudes. If this is not the case, an easy way to fix it is presented in SPSS - Recode with Value Labels Tool.
Second, we need to set 6 as a user missing value for our quality aspects. We'll do so with the syntax below. We'll take a look at our frequency distributions as well.
missing values sat1 to sat9 (6).
*Inspect histograms but don't create frequency tables again.
frequencies satov to sat9
/format notable /*DON'T CREATE ANY TABLES*/
/histogram.
Result
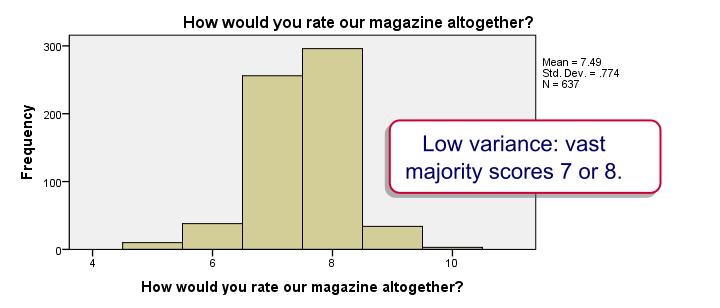
Our histograms don't show anything alarming except that many variables have rather low variances. This tends to result in rather limited correlations as we'll see in a minute.
Inspect Missing Values per Case
We'll now inspect how our missing values are distributed over cases with the syntax below.
compute mis1 = nmiss(satov to sat9).
*Apply variable label to new missingness variable.
variable labels mis1 "Number of (system or user) missings over satov to sat9".
*Inspect missing values per case.
frequencies mis1.
Result
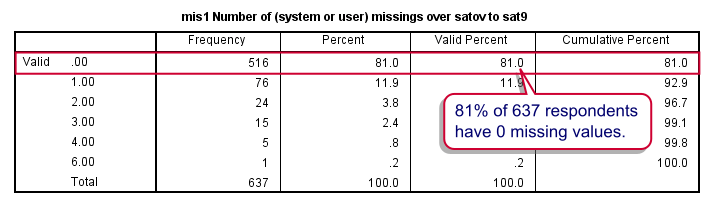
Cases with many missing values may complicate analyses and we find them suspicious. But then again, we'd like to use as much of our data as possible. If we don't allow any missings, we'll lose 19% of our sample. We therefore decide to exclude only cases with 4 or more missing values.
Filter Out Cases with 4 or More Missings
compute filt1 = (mis1 <= 3).
*Apply variable label to filter variable.
variable labels filt1 "Filter for 3 or fewer missings over satov to sat9".
*Activate filter variable.
filter by filt1.
*Check if filter works properly.
frequencies mis1.
Inspect Missing Values per Variable
We'll also take a look at how missings are distributed over our variables: do all variables have a sufficient number of valid values or do we need to exclude one or more variables from our analyses?
descriptives satov to sat9.
Result
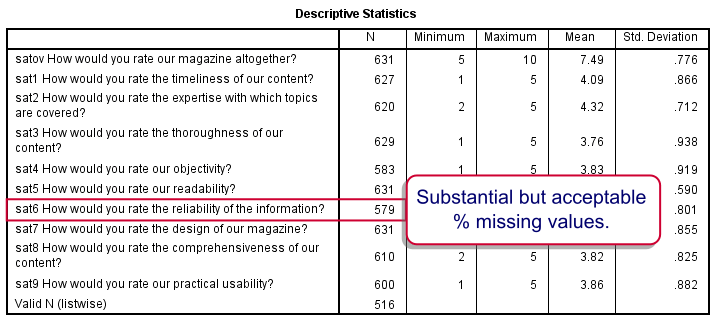
None of our variables seems problematic. The lowest N is seen for sat6 (reliability of information). Perhaps our respondents found this aspect hard to judge.
Inspect Pearson Correlations
Last but not least, we want to make sure our correlations look plausible. We'll take a quick look at the entire correlation matrix.
correlations satov to sat9.
*Save edited data file for regression.
save outfile 'magazine_reg.sav'.
Result
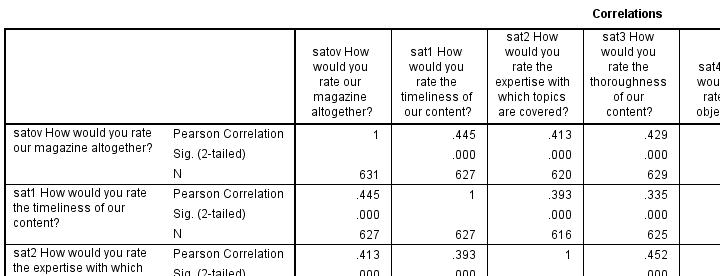
Things to watch out for are correlations in the “wrong” direction (positive where negative would make sense or reversely). This may result from some variables being positively coded and others negatively but we already saw that's not the case with our data.
Less common but very problematic are correlations close or equal to -1 or 1 which can result from (nearly) duplicate variables. This is not an issue here either.
We're now good to go for our regression analysis. Since we created a filter variable, we'll save our data as magazine_reg.sav. We'll use this file as input for our next tutorial.
SPSS Stepwise Regression Tutorial II
A large bank wants to gain insight into their employees’ job satisfaction. They carried out a survey, the results of which are in bank_clean.sav. The survey included some statements regarding job satisfaction, some of which are shown below.
Research Question
The main research question for today is which factors contribute (most) to overall job satisfaction? as measured by overall (“I'm happy with my job”). The usual approach for answering this is predicting job satisfaction from these factors with multiple linear regression analysis.2,6 This tutorial will explain and demonstrate each step involved and we encourage you to run these steps yourself by downloading the data file.
Data Check 1 - Coding
One of the best SPSS practices is making sure you've an idea of what's in your data before running any analyses on them. Our analysis will use overall through q9 and their variable labels tell us what they mean. Now, if we look at these variables in data view, we see they contain values 1 through 11.
So what do these values mean and -importantly- is this the same for all variables? A great way to find out is running the syntax below.
display dictionary
/variables overall to q9.
Result
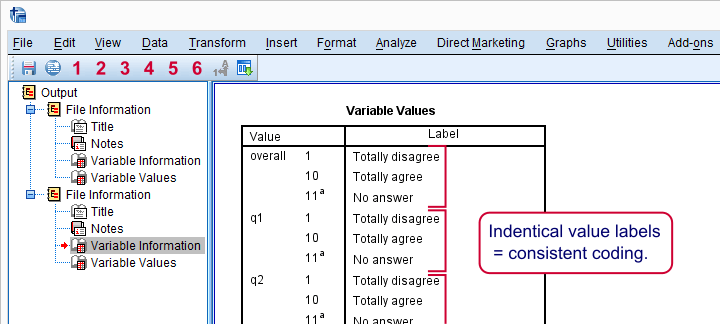
If we quickly inspect these tables, we see two important things:
- for all statemtents, higher values indicate stronger agreement;
- all statements are positive (“like” rather than “dislike”): more agreement indicates more positive sentiment.
Taking these findings together, we expect positive (rather than negative) correlations among all these variables. We'll see in a minute that our data confirm this.
Data Check 2 - Distributions
Our previous table suggests that all variables hold values 1 through 11 and 11 (“No answer”) has already been set as a user missing value. Now let's see if the distributions for these variables make sense by running some histograms over them.
frequencies overall to q9
/format notable
/histogram.
Data Check 3 - Missing Values
First and foremost, the distributions of all variables show values 1 through 10 and they look plausible. However, we have 464 cases in total but our histograms show slightly lower sample sizes. This is due to missing values. To get a quick idea to what extent values are missing, we'll run a quick DESCRIPTIVES table over them.
set tvars labels.
*2. Check for missings and listwise valid n.
descriptives overall to q9.
Result
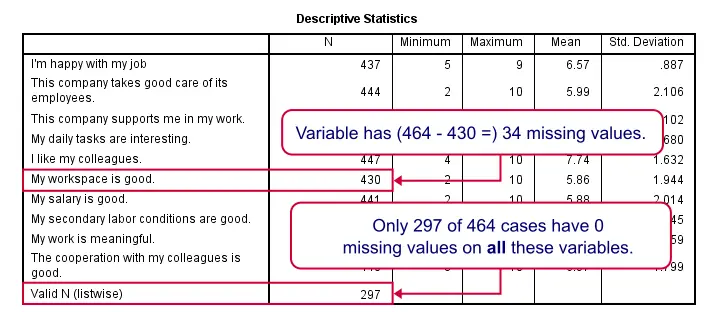
For now, we mostly look at N, the number of valid values for each variable. We see two important things:
- The lowest N is 430 (“My workspace is good”) out of 464 cases; roughly 7% of the values are missing.
- Only 297 cases have zero missing values on all variables in this table.
Correlations
We'll now inspect the correlations over our variables as shown below.
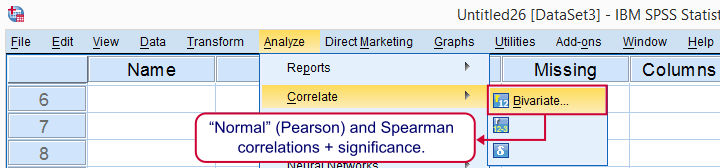
In the next dialog, we select all relevant variables and leave everything else as-is. We then click , resulting in the syntax below.
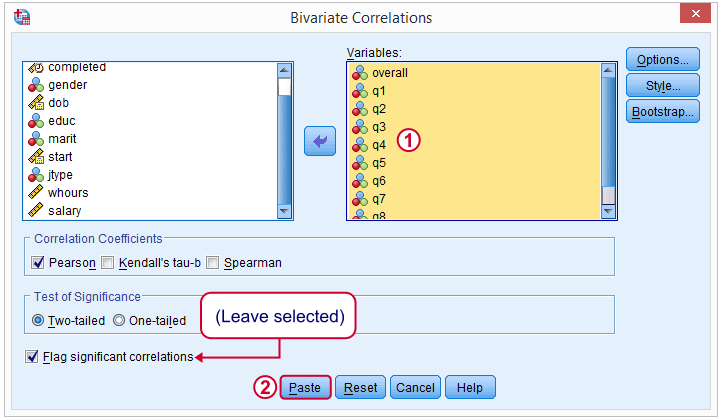
CORRELATIONS
/VARIABLES=overall q1 q2 q3 q4 q5 q6 q7 q8 q9
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE.
Importantly, note the last line -/MISSING=PAIRWISE.- here.
Result

Note that all correlations are positive -like we expected. Most correlations -even small ones- are statistically significant with p-values close to 0.000. This means there's a zero probability of finding this sample correlation if the population correlation is zero.
Second, each correlation has been calculated on all cases with valid values on the 2 variables involved, which is why each correlation has a different N. This is known as pairwise exclusion of missing values, the default for CORRELATIONS.
The alternative, listwise exclusion of missing values, would only use our 297 cases that don't have missing values on any of the variables involved. Like so, pairwise exclusion uses way more data values than listwise exclusion; with listwise exclusion we'd “lose” almost 36% or the data we collected.
Multiple Linear Regression - Assumptions
Simply “regression” usually refers to (univariate) multiple linear regression analysis and it requires some assumptions:1,4
- the prediction errors are independent over cases;
- the prediction errors follow a normal distribution;
- the prediction errors have a constant variance (homoscedasticity);
- all relations among variables are linear and additive.
We usually check our assumptions before running an analysis. However, the regression assumptions are mostly evaluated by inspecting some charts that are created when running the analysis.3 So we first run our regression and then look for any violations of the aforementioned assumptions.
Regression
Now that we're sure our data make perfect sense, we're ready for the actual regression analysis. We'll generate the syntax by following the screenshots below.
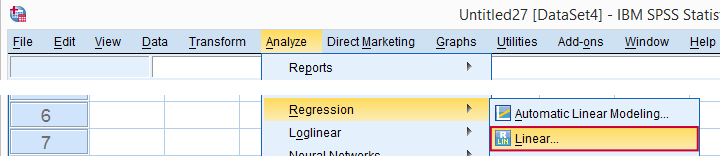
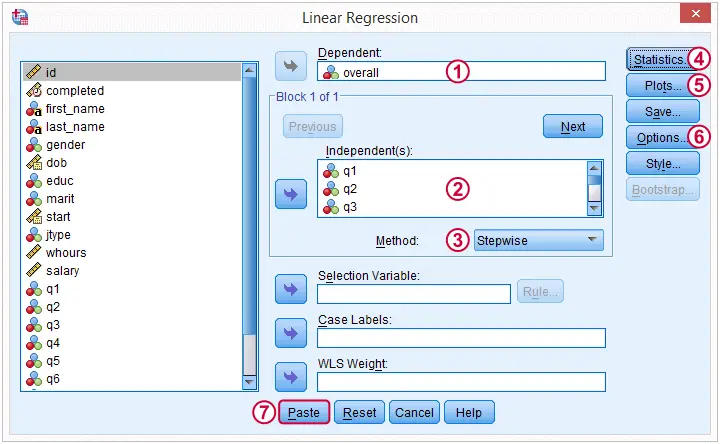
(We'll explain why we choose when discussing our output.)
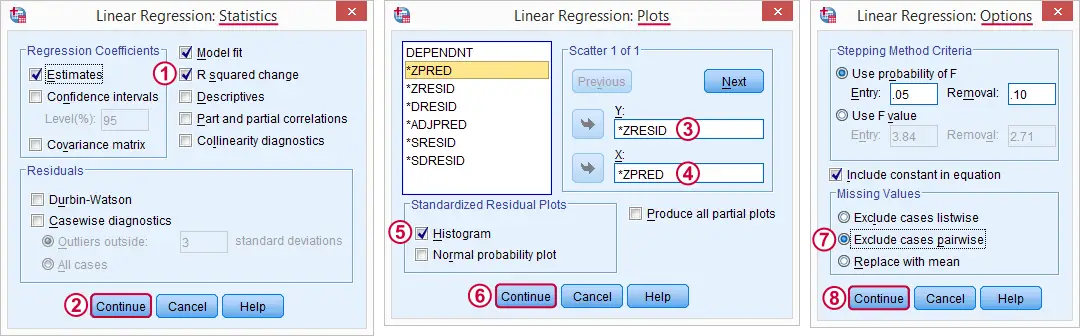
 -
- Here we select some charts for evaluation the regression assumptions.
Here we select some charts for evaluation the regression assumptions.
 By default, SPSS uses only our 297 complete cases for regression. By choosing this option, our regression will use the correlation matrix we saw earlier and thus use more of our data.
By default, SPSS uses only our 297 complete cases for regression. By choosing this option, our regression will use the correlation matrix we saw earlier and thus use more of our data.
“Stepwise” - What Does That Mean?
When we select the stepwise method, SPSS will include only “significant” predictors in our regression model: although we selected 9 predictors, those that don't contribute uniquely to predicting job satisfaction will not enter our regression equation. In doing so, it iterates through the following steps:
- find the predictor that contributes most to predicting the outcome variable and add it to the regression model if its p-value is below a certain threshold (usually 0.05).
- inspect the p-values of all predictors in the model. Remove predictors from the model if their p-values are above a certain threshold (usually 0.10);
- repeat this process until 1) all “significant” predictors are in the model and 2) no “non significant” predictors are in the model.
Regression Results - Coefficients Table
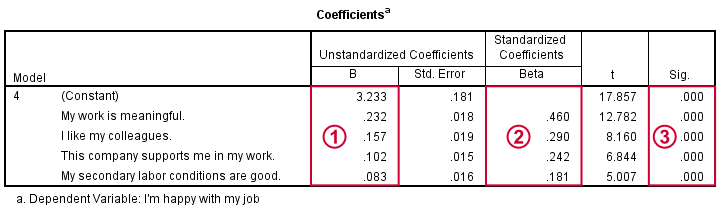
Our coefficients table tells us that SPSS performed 4 steps, adding one predictor in each. We usually report only the final model.
 Our unstandardized coefficients and the constant allow us to predict job satisfaction. Precisely,
Y' = 3.233 + 0.232 * x1 + 0.157 * x2 + 0.102 * x3 + 0.083 * x4
where Y' is predicted job satisfaction, x1 is meaningfulness and so on. This means that respondents who score 1 point higher on meaningfulness will -on average- score 0.23 points higher on job satisfaction.
Our unstandardized coefficients and the constant allow us to predict job satisfaction. Precisely,
Y' = 3.233 + 0.232 * x1 + 0.157 * x2 + 0.102 * x3 + 0.083 * x4
where Y' is predicted job satisfaction, x1 is meaningfulness and so on. This means that respondents who score 1 point higher on meaningfulness will -on average- score 0.23 points higher on job satisfaction.
Importantly, all predictors contribute positively (rather than negatively) to job satisfaction. This makes sense because they are all positive work aspects.
 If our predictors have different scales -not really the case here- we may compare their relative strengths -the beta coefficients- by standardizing them. Like so, we see that meaningfulness (.460) contributes about twice as much as colleagues (.290) or support (.242).
If our predictors have different scales -not really the case here- we may compare their relative strengths -the beta coefficients- by standardizing them. Like so, we see that meaningfulness (.460) contributes about twice as much as colleagues (.290) or support (.242).
 All predictors are highly statistically significant (p = 0.000), which is not surprising considering our large sample size and the stepwise method we used.
All predictors are highly statistically significant (p = 0.000), which is not surprising considering our large sample size and the stepwise method we used.
Regression Results - Model Summary
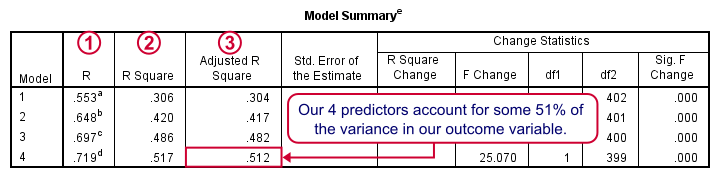
Adding each predictor in our stepwise procedure results in a better predictive accuracy.
 R is simply the Pearson correlation between the actual and predicted values for job satisfaction;
R is simply the Pearson correlation between the actual and predicted values for job satisfaction;
 R square -the squared correlation- is the proportion of variance in job satisfaction accounted for by the predicted values;
R square -the squared correlation- is the proportion of variance in job satisfaction accounted for by the predicted values;
 We typically see that our regression equation performs better in the sample on which it's based than in our population. tries to estimate the predictive accuracy in our population and is slightly lower than R square.
We typically see that our regression equation performs better in the sample on which it's based than in our population. tries to estimate the predictive accuracy in our population and is slightly lower than R square.
We'll probably settle for -and report on- our final model; the coefficients look good it predicts job performance best.
Regression Results - Residual Histogram
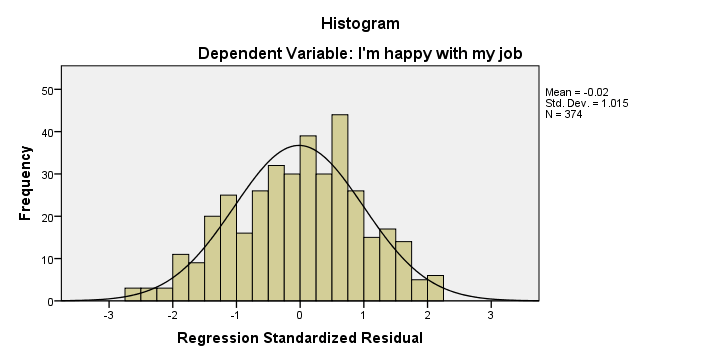
Remember that one of our regression assumptions is that the residuals (prediction errors) are normally distributed. Our histogram suggests that this more or less holds, although it's a little skewed to the left.
Regression Results - Residual Plot
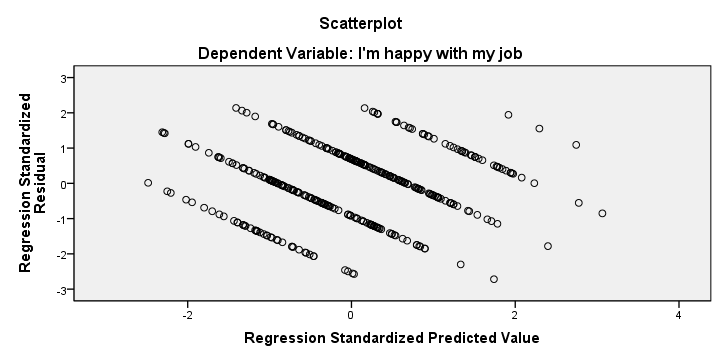
We also created a scatterplot with predicted values on the x-axis and residuals on the y-axis. This chart does not show violations of the independence, homoscedasticity and linearity assumptions but it's not very clear.
We mostly see a striking pattern of descending straight lines. This is because our dependent variable only holds values 1 through 10. Therefore, each predicted value and its residual always add up to 1, 2 and so on. Standardizing both variables may change the scales of our scatterplot but not its shape.
Stepwise Regression - Reporting
There's no full consensus on how to report a stepwise regression analysis.5,7 As a basic guideline, include
- a table with descriptive statistics;
- the correlation matrix of the dependents variable and all (candidate) predictors;
- the model summary table with R square and change in R square for each model;
- the coefficients table with at least the B and β coefficients and their p-values.
Regarding the correlations, we'd like to have statistically significant correlations flagged but we don't need their sample sizes or p-values. Since you can't prevent SPSS from including the latter, try SPSS Correlations in APA Format.
You can further edit the result fast in an OpenOffice or Excel spreadsheet by right clicking the table and selecting
 .
.
I guess that's about it. I hope you found this tutorial helpful. Thanks for reading!
References
- Stevens, J. (2002). Applied multivariate statistics for the social sciences. Mahway, NJ: Lawrence Erlbaum Associates.
- Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
- Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
- Berry, W.D. (1993). Understanding Regression Assumptions. Newbury Park, CA: Sage.
- Field, A. (2013). Discovering Statistics with IBM SPSS Newbury Park, CA: Sage.
- Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
- Nicol, A.M. & Pexman, P.M. (2010). Presenting Your Findings. A Practical Guide for Creating Tables. Washington: APA.
 SPSS TUTORIALS
SPSS TUTORIALS