- Covariance - What is It?
- Covariance or Correlation?
- Sample Covariance Formula
- Covariance Calculation Example
- Software for Computing Covariances
Covariance - What is It?
A covariance is basically an unstandardized correlation. That is: a covariance is a number that indicates to what extent 2 variables are linearly related. In contrast to a (Pearson) correlation, however, a covariance depends on the scales of both variables involved as expressed by their standard deviations.
The figure below visualizes some correlations and covariances as scatterplots.
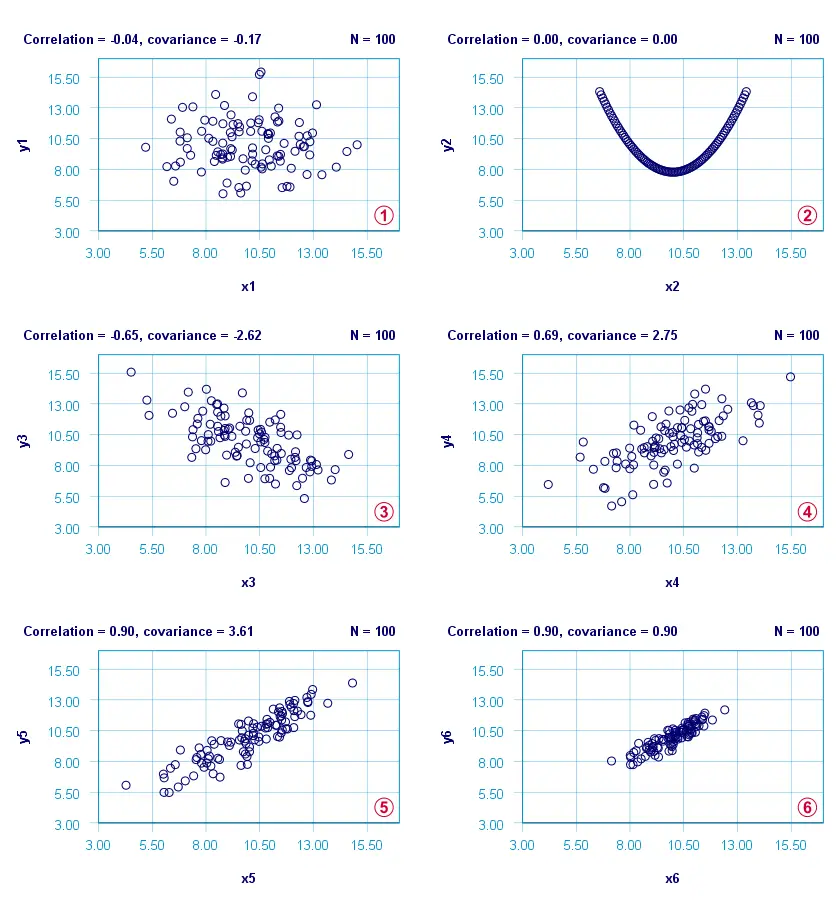
 x1 and y1 are basically unrelated. The covariance and correlation are both close to zero;
x1 and y1 are basically unrelated. The covariance and correlation are both close to zero;
 x2 and y2 are strongly related but not linearly at all. The covariance and correlation are zero.
x2 and y2 are strongly related but not linearly at all. The covariance and correlation are zero.
 x3 and y3 are negatively related. The covariance and correlation are both negative;
x3 and y3 are negatively related. The covariance and correlation are both negative;
 x4 and y4 are positively related. The covariance and correlation are both positive;
x4 and y4 are positively related. The covariance and correlation are both positive;
 x5 and y5 are strongly positively related. Because they have the same standard deviations as x4 and y4, the correlation and covariance both increase;
x5 and y5 are strongly positively related. Because they have the same standard deviations as x4 and y4, the correlation and covariance both increase;
 x6 and y6 are identical to x5 and y5 except that their standard deviations are 1.0 instead of 2.0. This shrinks the covariance with a factor 4.0 but does not affect the correlation.
x6 and y6 are identical to x5 and y5 except that their standard deviations are 1.0 instead of 2.0. This shrinks the covariance with a factor 4.0 but does not affect the correlation.
Comparing plots  and
and  emphasizes that covariances are scale dependent whereas correlations aren't. This may make you wonder
why should I ever compute a covariance
emphasizes that covariances are scale dependent whereas correlations aren't. This may make you wonder
why should I ever compute a covariance
instead of a correlation?
Covariance or Correlation?
First off, the precise relation between a covariance and correlation is given by
$$S_{xy} = r_{xy} \cdot s_x \cdot s_y$$
where
- \(S_{xy}\) denotes the (sample) covariance between variables \(X\) and \(Y\);
- \(r_{xy}\) denotes the (Pearson) correlation between \(X\) and \(Y\);
- \(s_x\) and \(s_y\) denote the (sample) standard deviations of \(X\) and \(Y\).
This formula shows that a covariance can be seen as a correlation that's “weighted” by the product of the standard deviations of the 2 variables involved: everything else equal, larger standard deviations result in larger covariances.
This feature may be desirable for comparing associations among variable pairs. This only makes sense if all variables are measured on identical scales such as dollars, seconds or kilos. Some analyses that require covariances are the following:
1. Cronbach’s alpha is usually computed on covariances instead of correlations. This is because scale scores are computed as sums or means over unstandardized variables. Therefore, variables with larger SD's have more impact on scale scores. This is why associations among such variables also have more weight in the computation of Cronbach's alpha.
2. In factor analysis, a covariance matrix is sometimes analyzed instead of a correlation matrix. If so, associations among variables have more impact on the factor solution insofar as these variables have larger SD's.
3. Some analyses need to meet the assumption of equal covariance matrices over subpopulations. An example is MANOVA, in which the Box test -basically a multivariate expansion of Levene's test- is often used for testing this assumption.
4. Somewhat surprisingly, ANCOVA -meaning analysis of covariance- does not involve computing covariances.
So those are some analyses that involve covariances. So how are these computed? Well, which formula to use depends on which type of data you're analyzing.
Sample Covariance Formula
If your data contain a sample from a much larger population (usually the case), the sample covariance is computed as
$$S_{xy} = \frac{\sum\limits_{i = 1}^N(X_i - \overline{X})(Y_i - \overline{Y})}{N - 1}$$
where
- \(S_{xy}\) denotes the (sample) covariance between variables \(X\) and \(Y\);
- \(\overline{X}\) and \(\overline{Y}\) denote the sample means for \(X\) and \(Y\);
- \(N\) denotes the total sample size.
Let's now get a grip on this formula by using it in a calculation example.
Covariance Calculation Example
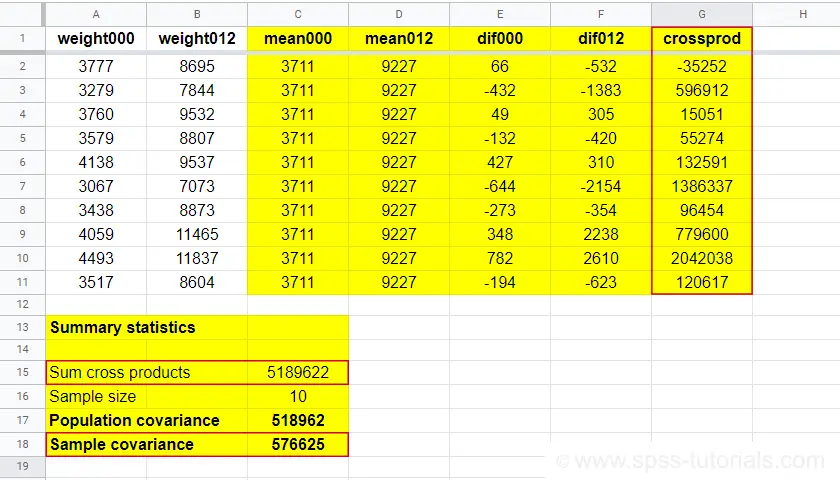
The table below contains the weights in grams of 10 babies at birth (X) and at age 12 months (Y). What's the covariance between X and Y?
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 3777 | 3279 | 3760 | 3579 | 4138 | 3067 | 3438 | 4059 | 4493 | 3517 |
| Y | 8695 | 7844 | 9532 | 8807 | 9537 | 7073 | 8873 | 11465 | 11837 | 8604 |
First off,
- the sample size is \(N\) = 10 and the means are
- \(\overline{X}\) = 3711 and
- \(\overline{Y}\) = 9227.
Therefore,
$$S_{xy} = \frac{(3777 - 3711)\cdot(8695 - 9227)\;+\;...\;+\;(3517 - 3711)\cdot(8604 - 9227)}{10 - 1}$$
$$S_{xy} = \frac{66 \cdot -532\;+\;...\;+\;-194 \cdot -623}{10 - 1}$$
$$S_{xy} = \frac{5189622}{10 - 1} = 576625$$
You can look up the entire calculation in this Googlesheet, partly shown below.
Population Covariance Formula
If your data hold the entire population you'd like to study, you can compute the covariance as
$$\sigma_{xy} = \frac{\sum\limits_{i = 1}^N(X_i - \mu_x)(Y_i - \mu_Y)}{N}$$
where
- \(\sigma_{xy}\) denotes the (population) covariance between variables \(X\) and \(Y\);
- \(\mu_x\) and \(\mu_y\) denote the population means for \(X\) and \(Y\);
- \(N\) denotes the population size.
Software for Computing Covariances
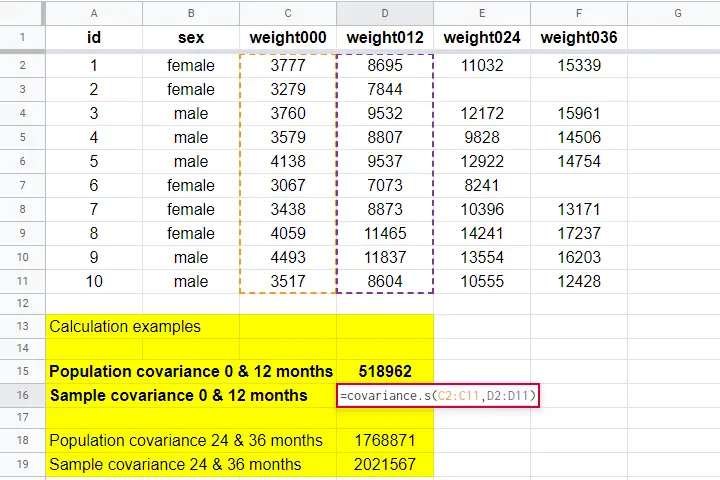
Both sample and population covariances are easily computed in Googlesheets and Excel. This Googlesheet, partly shown below, contains a couple of examples.
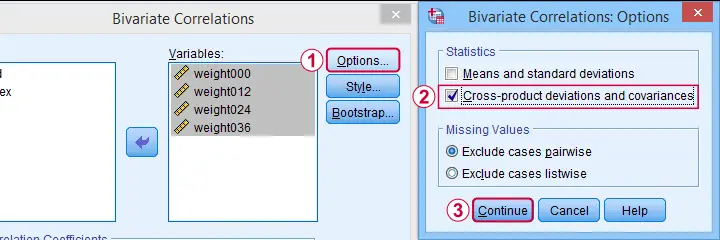
A full covariance matrix for several variables is easily obtained from SPSS. However, “covariance” in SPSS always refers to the sample covariance because
the population covariance is completely absent from SPSS.
Pretty poor for a “statistical package”. But anyway: the only menu based option for this is

 as illustrated below.
as illustrated below.
A much better option, however, is using SPSS syntax like we did in Cronbach’s Alpha in SPSS. This is faster and results in a much nicer table layout as shown below.
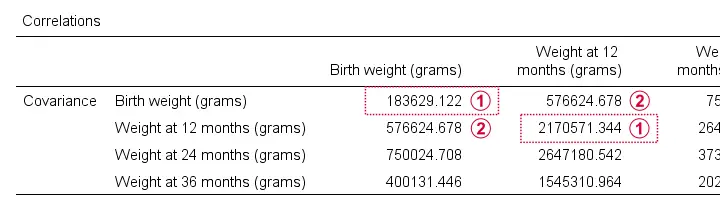
Two quick notes are in place here:
 Just like a correlation matrix, a covariance matrix is symmetrical: the covariance between X and Y is obviously equal to that between Y and X.
Just like a correlation matrix, a covariance matrix is symmetrical: the covariance between X and Y is obviously equal to that between Y and X.
 The main diagonal contains the covariances between each variable and itself. These are simply the variances (squared standard deviations) of our variables. This last point implies that
we can compute a correlation matrix from a covariance matrix
The main diagonal contains the covariances between each variable and itself. These are simply the variances (squared standard deviations) of our variables. This last point implies that
we can compute a correlation matrix from a covariance matrix
but not reversely.
For example, the correlation between our first 2 variables is
$$r_{xy} = \frac{576625}{\sqrt{183629} \cdot \sqrt{2170571}} = 0.913$$
Right. I guess that should do regarding covariances. If you've any feedback, please throw us a comment below. Other than that:
thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 12 COMMENTS:
By Jon K Peck on September 24th, 2021
With pivot table output, you get full-precision values, and you have control over the formatting.
However, all the tables have the same OMS subtype of 'Matrix Table', which makes it harder to automate formatting and reuse as data.
The OMS command identifier is, as you would expect, MATRIX. You can get at individual tables with OUTPUT MODIFY using IF LABELS or various OMS properties, however, and tableLooks and pivoting are available.
By Ruben Geert van den Berg on September 25th, 2021
Hi Peninah!
Thanks for the compliment! Sorry but I haven't used R for ages so I can't help you with that.
Kind regards,
SPSS tutorials
By Ruben Geert van den Berg on September 25th, 2021
That sounds great! The issues with OMS sound as very minor ones... I often do some of the editing in Excel anyway.
PROCESS is not high on my agenda but as soon as I need it for one of my students, I'm going to experiment heavily with it.
P.s. the PROCESS macro should have been named !PROCESS rather than PROCESS. One of my tools uses PROCESS as a normal syntax keyword and this triggers the PROCESS macro whenever it's been defined... But perhaps I'd better bother Andrew Hayes with that at some point...
By Kidest woldu on December 26th, 2022
It's good!
We can check the covariance using the correlation but we can not check the correlation using the covariance, it's a great idea.
And in the SPSS software we can not do the population covariance.
By Jon Peck on December 28th, 2022
It is very rare, in my experience, for someone to need a population covariance calculation. In fact, understanding whether you have a sample or the entire population of interest can be confusing. But the difference in the calculation is negligable with any reasonable sample size. The calculation, though, could be done with MATRIX.