• Summary
• Wrong Covariances from FACTOR
• Correct Covariances from CORRELATIONS
• Correct Covariances from REGRESSION

Summary

When using pairwise exclusion of missing values, SPSS FACTOR computes wrong covariances. For correct covariances, use

• CORRELATIONS (menu or syntax) or
• REGRESSION (syntax only).

This tutorial presents a quick comparison of these 3 methods. We'll use baby-weights.sav -partly shown below- for all examples.

Wrong Covariances from FACTOR

Right. So let's compute the covariance matrix for weight000 through weight036 by using FACTOR. The SPSS syntax below does so using pairwise exclusion of missing values.

Result

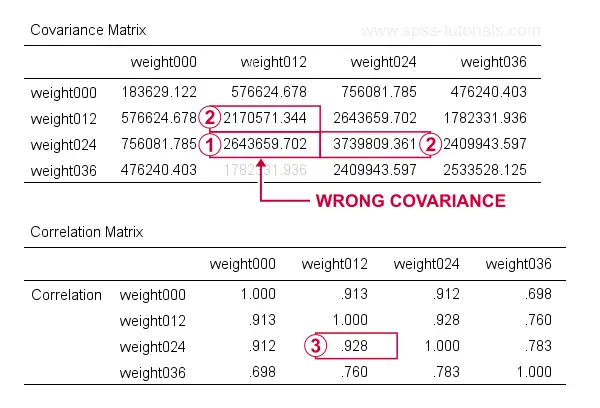
At first, these results look perfect. Now, let's recompute the covariance between weight012 and weigh024 from the variances and the correlation for these variables by using

$$S_{xy} = r_{xy} \cdot s_x \cdot s_y$$

where

• \(S_{xy}\) denotes the (sample) covariance between variables \(X\) and \(Y\);
• \(r_{xy}\) denotes the (Pearson) correlation between \(X\) and \(Y\);
• \(s_x\) and \(s_y\) denote the (sample) standard deviations of \(X\) and \(Y\).

This gives

$$S_{xy} = 0.928 \cdot \sqrt{2170571} \cdot \sqrt{3739809} = 2643660$$

which is indeed what SPSS reports here. So how could this possibly be wrong? Our second approach will clarify just that and come up with different -but correct- results.

Correct Covariances from CORRELATIONS

The only way to obtain covariances from SPSS’ menu is by navigating to Analyze Correlate Bivariate as shown below.

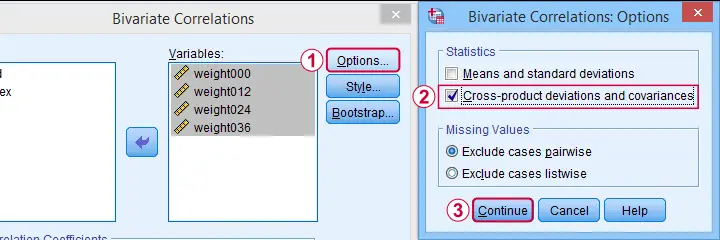
This results in the syntax below. Let's run it.

Result

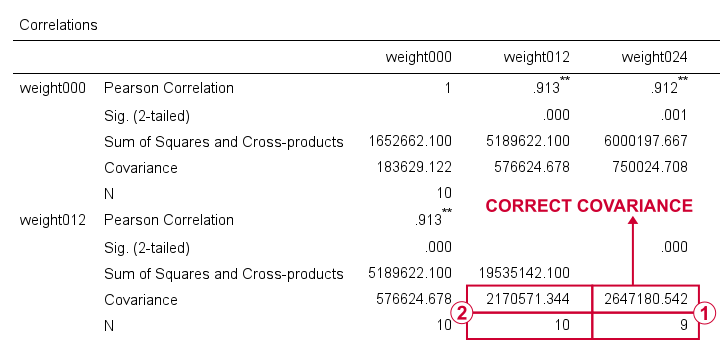
For weight012 and weight024, SPSS reports \(S_{xy}\) = 2647181. Note that this is based on a subsample of N = 9 cases due to pairwise exclusion of missing values.
The variance for weight012, however, is based on a different subsample of N = 10...

...and that's why the previous results were wrong. FACTOR seems to compute each covariance from a correlation and two variances that may all be based on different subsamples!

CORRELATIONS, however, correctly computes all components for a covariance on the same subsample: all cases having valid values on both variables. Alternative software such as Excel and Googlesheets also comply with this approach.

I think these results provide sufficient evidence for my claim that FACTOR may compute wrong covariances. Nevertheless, let's see what our third -and best- method for obtaining covariances comes up with...

Correct Covariances from REGRESSION

The syntax below illustrates how to obtain covariances and the sample sizes they're based on via REGRESSION.

Result

Although the multiple regression results aren't helpful, the previous syntax does result in a nice and clean covariance matrix as shown below.

First off, note that REGRESSION comes up with the same (correct) covariances as CORRELATIONS. So that makes 1 against 2 -or more if we take Excel and/or Googlesheets into account.

Second, note that REGRESSION results in a convenient table layout that's sorted by statistic rather than by variable. This usually comes in handy for further processing such as

• computing Cronbach’s alpha or
• some kind of factor analysis.

So that's basically it. Let me know what you think by throwing in a comment below. We always appreciate some feedback. Also if you think our tutorials totally suck.

Thanks for reading!