Quick Definition

Z-scores are scores that have mean = 0
and standard deviation = 1. Z-scores are also known as standardized scores because they are scores that have been given a common standard. This standard is a mean of zero and a standard deviation of 1.

Contrary to what many people believe, z-scores are not necessarily normally distributed.

Z-Scores - Example

A group of 100 people took some IQ test. My score was 5. So is that good or bad? At this point, there's no way of telling because we don't know what people typically score on this test. However, if my score of 5 corresponds to a z-score of 0.91, you'll know it was pretty good: it's roughly a standard deviation higher than the average (which is always zero for z-scores).
What we see here is that standardizing scores facilitates the interpretation of a single test score. Let's see how that works.

Scores - Histogram

A quick peek at some of our 100 scores on our first IQ test shows a minimum of 1 and a maximum of 6. However, we'll gain much more insight into these scores by inspecting their histogram as shown below.

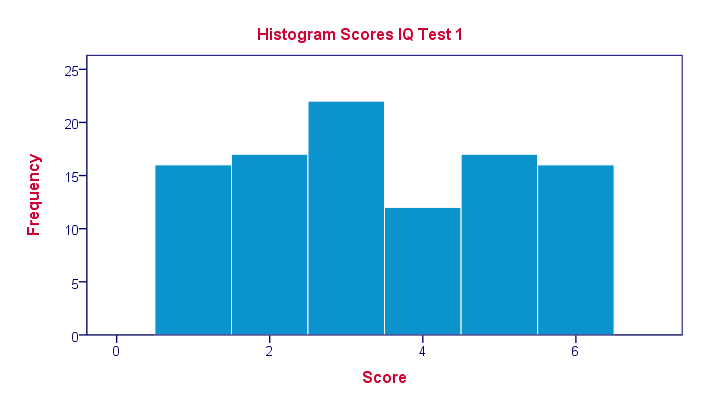
The histogram confirms that scores range from 1 through 6 and each of these scores occurs about equally frequently. This pattern is known as a uniform distribution and we typically see this when we roll a die a lot of times: numbers 1 through 6 are equally likely to come up. Note that these scores are clearly not normally distributed.

Z-Scores - Standardization

We suggested earlier on that giving scores a common standard of zero mean and unity standard deviation facilitates their interpretation. We can do just that by

• first subtracting the mean over all scores from each individual score and
• then dividing each remainder by the standard deviation over all scores.

These two steps are the same as the following formula:
$$Z_x = \frac{X_i - \overline{X}}{S_x}$$
As shown by the table below, our 100 scores have a mean of 3.45 and a standard deviation of 1.70. By entering these numbers into the formula, we see why a score of 5 corresponds to a z-score of 0.91:
$$Z_x = \frac{5 - 3.45}{1.70} = 0.91$$
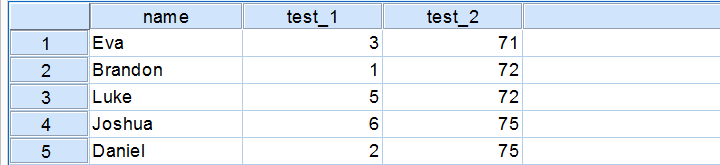
In a similar vein, the screenshot below shows the z-scores for all distinct values of our first IQ test added to the data.

Z-Scores - Histogram

In practice, we obviously have some software compute z-scores for us. We did so and ran a histogram on our z-scores, which is shown below. 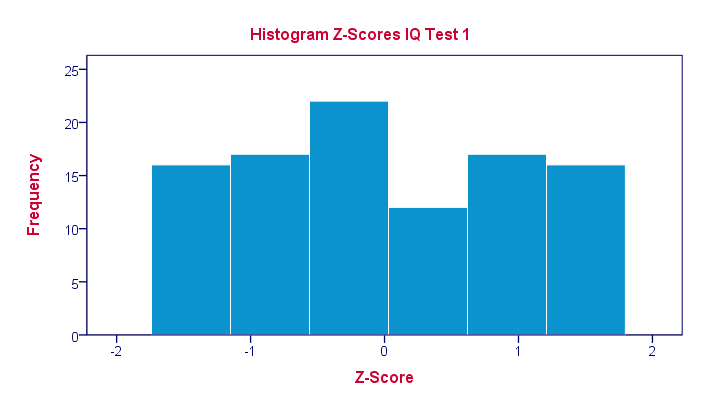If you look closely, you'll notice that the z-scores indeed have a mean of zero and a standard deviation of 1. Other than that, however, z-scores follow the exact same distribution as original scores. That is, standardizing scores doesn't make their distribution more “normal” in any way.

What's a Linear Transformation?

Z-scores are linearly transformed scores. What we mean by this, is that if we run a scatterplot of scores versus z-scores, all dots will be exactly on a straight line (hence, “linear”). The scatterplot below illustrates this. It contains 100 points but many end up right on top of each other.

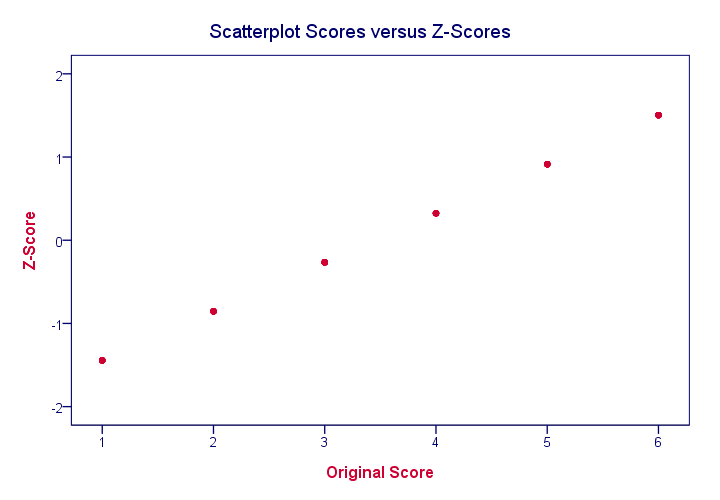
In a similar vein, if we had plotted scores versus squared scores, our line would have been curved; in contrast to standardizing, taking squares is a non linear transformation.

Z-Scores and the Normal Distribution

We saw earlier that standardizing scores doesn't change the shape of their distribution in any way; distribution don't become any more or less “normal”. So why do people relate z-scores to normal distributions?

The reason may be that many variables actually do follow normal distributions. Due to the central limit theorem, this holds especially for test statistics. If a normally distributed variable is standardized, it will follow a standard normal distribution.

This is a common procedure in statistics because values that (roughly) follow a standard normal distribution are easily interpretable. For instance, it's well known that some 2.5% of values are larger than two and some 68% of values are between -1 and 1.

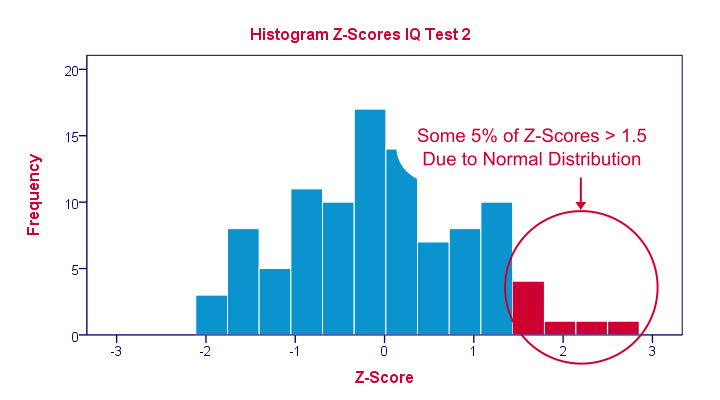
The histogram below illustrates this: if a variable is roughly normally distributed, z-scores will roughly follow a standard normal distribution. For z-scores, it always holds (by definition) that a score of 1.5 means “1.5 standard deviations higher than average”. However, if a variable also follows a standard normal distribution, then we also know that 1.5 roughly corresponds to the 95th percentile.

Z-Scores in SPSS

SPSS users can easily add z-scores to their data by using a DESCRIPTIVES command as in descriptives test_1 test_2/save. in which “save” means “save z-scores as new variables in my data”. For more details, see z-scores in SPSS.