SPSS Simple Linear Regression Tutorial

1. Create Scatterplot with Fit Line
2. SPSS Linear Regression Dialogs
3. Interpreting SPSS Regression Output
4. Evaluating the Regression Assumptions
5. APA Guidelines for Reporting Regression

Research Question and Data

Company X had 10 employees take an IQ and job performance test. The resulting data -part of which are shown below- are in simple-linear-regression.sav.

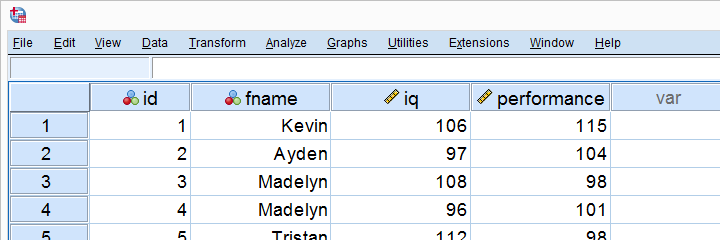
The main thing Company X wants to figure out is does IQ predict job performance? And -if so- how? We'll answer these questions by running a simple linear regression analysis in SPSS.

Create Scatterplot with Fit Line

A great starting point for our analysis is a scatterplot. This will tell us if the IQ and performance scores and their relation -if any- make any sense in the first place. We'll create our chart from Graphs Legacy Dialogs Scatter/Dot and we'll then follow the screenshots below.

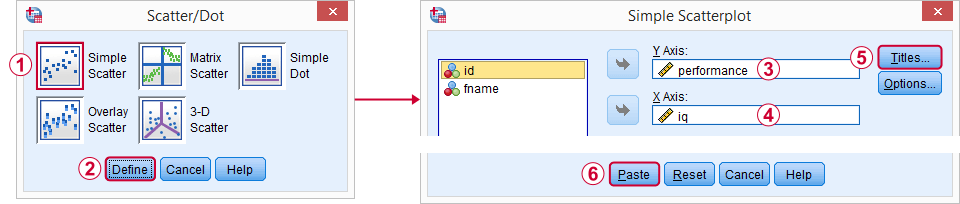
I personally like to throw in

• a title that says what my audience are basically looking at and
• a subtitle that says which respondents or observations are shown and how many.

Walking through the dialogs resulted in the syntax below. So let's run it.

SPSS Scatterplot with Titles Syntax

Result

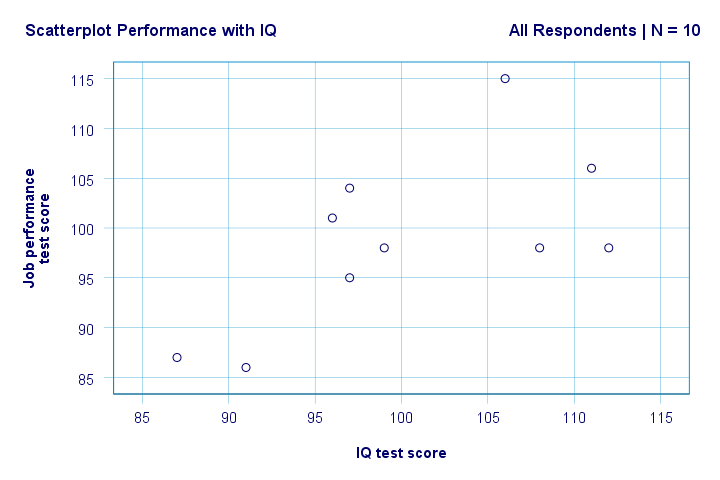
Right. So first off, we don't see anything weird in our scatterplot. There seems to be a moderate correlation between IQ and performance: on average, respondents with higher IQ scores seem to be perform better. This relation looks roughly linear.
Let's now add a regression line to our scatterplot. Right-clicking it and selecting Edit content In Separate Window opens up a Chart Editor window. Here we simply click the “Add Fit Line at Total” icon as shown below.

By default, SPSS now adds a linear regression line to our scatterplot. The result is shown below.

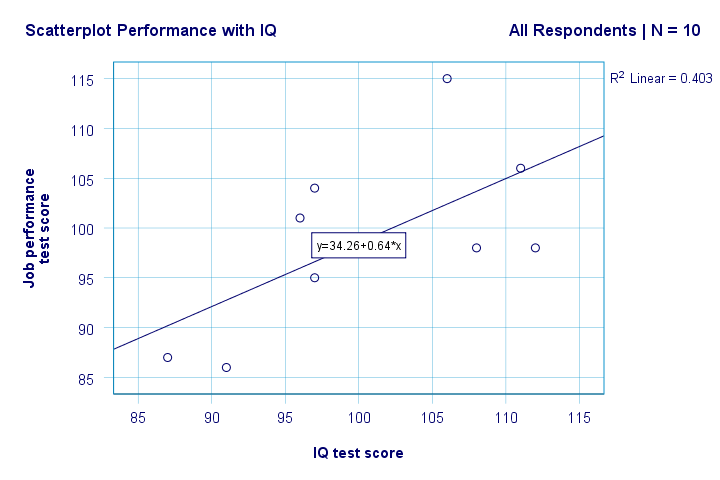
We now have some first basic answers to our research questions. R² = 0.403 indicates that IQ accounts for some 40.3% of the variance in performance scores. That is, IQ predicts performance fairly well in this sample.
But how can we best predict job performance from IQ? Well, in our scatterplot y is performance (shown on the y-axis) and x is IQ (shown on the x-axis). So that'll be performance = 34.26 + 0.64 * IQ. So for a job applicant with an IQ score of 115, we'll predict 34.26 + 0.64 * 115 = 107.86 as his/her most likely future performance score.
Right, so that gives us a basic idea about the relation between IQ and performance and presents it visually. However, a lot of information -statistical significance and confidence intervals- is still missing. So let's go and get it.

SPSS Linear Regression Dialogs

Rerunning our minimal regression analysis from Analyze Regression Linear gives us much more detailed output. The screenshots below show how we'll proceed.

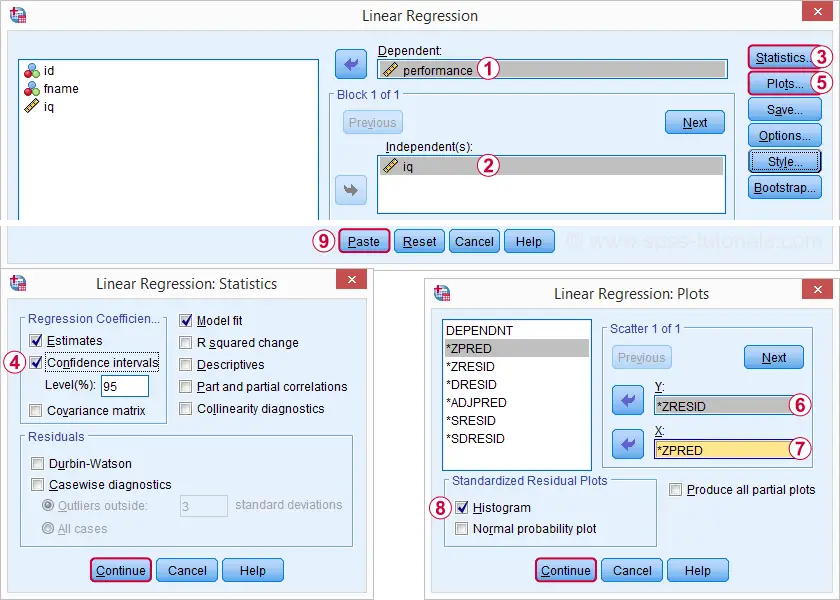
Selecting these options results in the syntax below. Let's run it.

SPSS Simple Linear Regression Syntax

SPSS Regression Output I - Coefficients

Unfortunately, SPSS gives us much more regression output than we need. We can safely ignore most of it. However, a table of major importance is the coefficients table shown below.

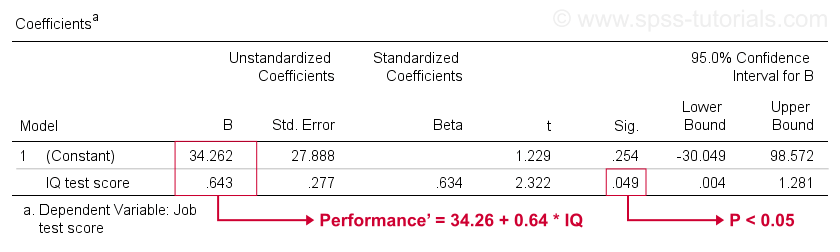
This table shows the B-coefficients we already saw in our scatterplot. As indicated, these imply the linear regression equation that best estimates job performance from IQ in our sample.
Second, remember that we usually reject the null hypothesis if p < 0.05. The B coefficient for IQ has “Sig” or p = 0.049. It's statistically significantly different from zero.
However, its 95% confidence interval -roughly, a likely range for its population value- is [0.004,1.281]. So B is probably not zero but it may well be very close to zero. The confidence interval is huge -our estimate for B is not precise at all- and this is due to the minimal sample size on which the analysis is based.

SPSS Regression Output II - Model Summary

Apart from the coefficients table, we also need the Model Summary table for reporting our results.

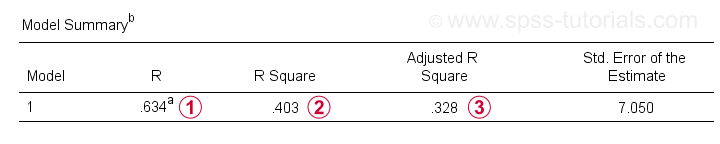
R is the correlation between the regression predicted values and the actual values. For simple regression, R is equal to the correlation between the predictor and dependent variable.
R Square -the squared correlation- indicates the proportion of variance in the dependent variable that's accounted for by the predictor(s) in our sample data.
Adjusted R-square estimates R-square when applying our (sample based) regression equation to the entire population.

Adjusted r-square gives a more realistic estimate of predictive accuracy than simply r-square. In our example, the large difference between them -generally referred to as shrinkage- is due to our very minimal sample size of only N = 10.

In any case, this is bad news for Company X: IQ doesn't really predict job performance so nicely after all.

Evaluating the Regression Assumptions

The main assumptions for regression are

1. Independent observations;
2. Normality: errors must follow a normal distribution in population;
3. Linearity: the relation between each predictor and the dependent variable is linear;
4. Homoscedasticity: errors must have constant variance over all levels of predicted value.

1. If each case (row of cells in data view) in SPSS represents a separate person, we usually assume that these are “independent observations”. Next, assumptions 2-4 are best evaluated by inspecting the regression plots in our output.

2. If normality holds, then our regression residuals should be (roughly) normally distributed. The histogram below doesn't show a clear departure from normality.

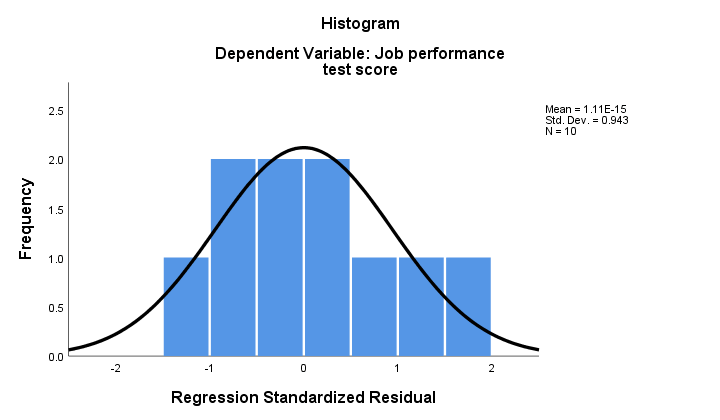
The regression procedure can add these residuals as a new variable to your data. By doing so, you could run a Kolmogorov-Smirnov test for normality on them. For the tiny sample at hand, however, this test will hardly have any statistical power. So let's skip it.

The 3. linearity and 4. homoscedasticity assumptions are best evaluated from a residual plot. This is a scatterplot with predicted values in the x-axis and residuals on the y-axis as shown below. Both variables have been standardized but this doesn't affect the shape of the pattern of dots.

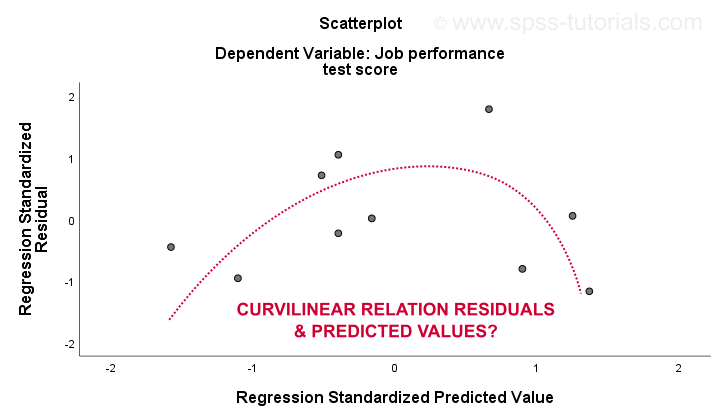
Honestly, the residual plot shows strong curvilinearity. I manually drew the curve that I think fits best the overall pattern. Assuming a curvilinear relation probably resolves the heteroscedasticity too but things are getting way too technical now. The basic point is simply that some assumptions don't hold. The most common solutions for these problems -from worst to best- are

• ignoring these assumptions altogether;
• lying that the regression plots don't indicate any violations of the model assumptions;
• a non linear transformation -such as logarithmic- to the dependent variable;
• fitting a curvilinear model -which we'll give a shot in a minute.

APA Guidelines for Reporting Regression

The figure below is -quite literally- a textbook illustration for reporting regression in APA format.

Creating this exact table from the SPSS output is a real pain in the ass. Editing it goes easier in Excel than in WORD so that may save you a at least some trouble.
Alternatively, try to get away with copy-pasting the (unedited) SPSS output and pretend to be unaware of the exact APA format.

Non Linear Regression Experiment

Our sample size is too small to really fit anything beyond a linear model. But we did so anyway -just curiosity. The easiest option in SPSS is under Analyze Regression Curve Estimation. We're not going to discuss the dialogs but we pasted the syntax below.

SPSS Non Linear Regression Syntax

Results

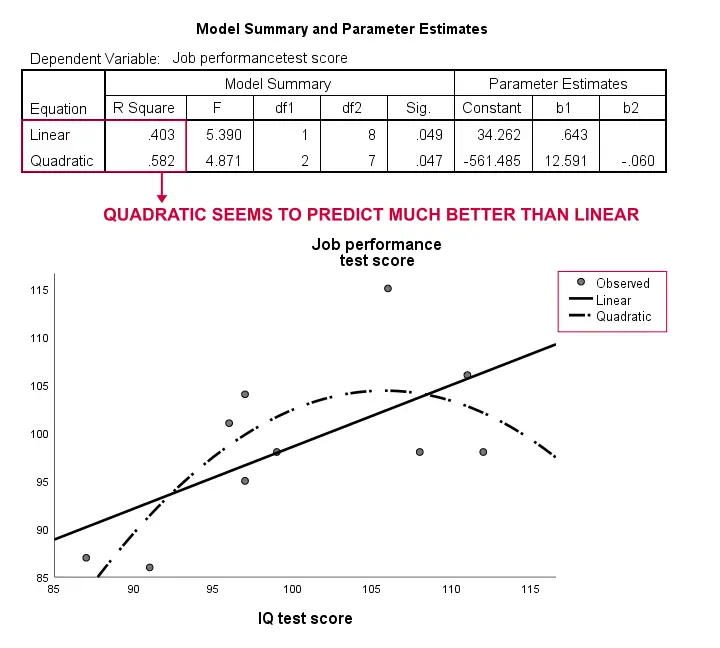
Again, our sample is way too small to conclude anything serious. However, the results do kinda suggest that a curvilinear model fits our data much better than the linear one. We won't explore this any further but we did want to mention it; we feel that curvilinear models are routinely overlooked by social scientists.

Thanks for reading!

Simple Linear Regression – Quick Introduction

• Correlation
• B Coefficients
• Intercept
• Regression Residuals
• R-Square

Simple linear regression is a technique that predicts a metric variable from a linear relation with another metric variable. Remember that “metric variables” refers to variables measured at interval or ratio level. The point here is that calculations -like addition and subtraction- are meaningful on metric variables (“salary” or “length”) but not on categorical variables (“nationality” or “color”).

Example: Predicting Job Performance from IQ

Some company wants to know can we predict job performance from IQ scores? The very first step they should take is to measure both (job) performance and IQ on as many employees as possible. They did so on 10 employees and the results are shown below.

Looking at these data, it seems that employees with higher IQ scores tend to have better job performance scores as well. However, this is difficult to see with even 10 cases -let alone more. The solution to this is creating a scatterplot as shown below.

Scatterplot Performance with IQ

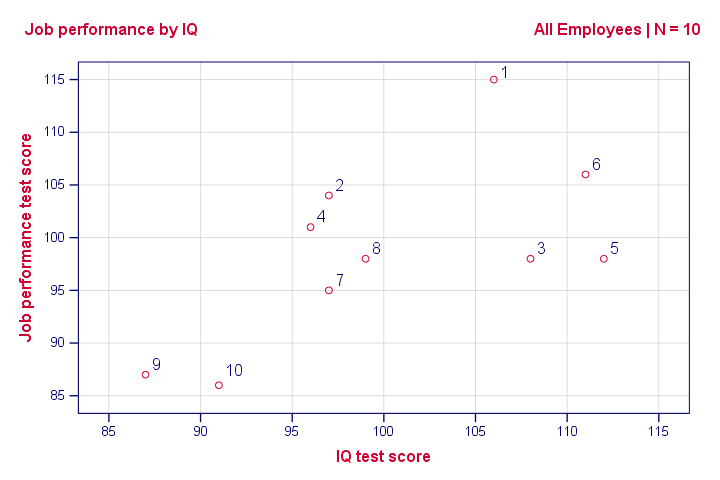
Note that the id values in our data show which dot represents which employee. For instance, the highest point (best performance) is 1 -Kevin, with a performance score of 115.
So anyway, if we move from left to right (lower to higher IQ), our dots tend to lie higher (better performance). That is, our scatterplot shows a positive (Pearson) correlation between IQ and performance.

Pearson Correlation Performance with IQ

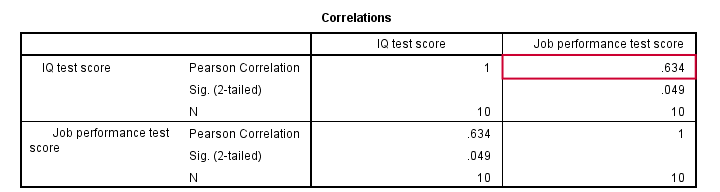
As shown in the previous figure, the correlation is 0.63. Despite our small sample size, it's even statistically significant because p < 0.05. There's a strong linear relation between IQ and performance. But what we haven't answered yet is: how can we predict performance from IQ? We'll do so by assuming that the relation between them is linear. Now the exact relation requires just 2 numbers -and intercept and slope- and regression will compute them for us.

Linear Relation - General Formula

Any linear relation can be defined as Y’ = A + B * X. Let's see what these numbers mean.

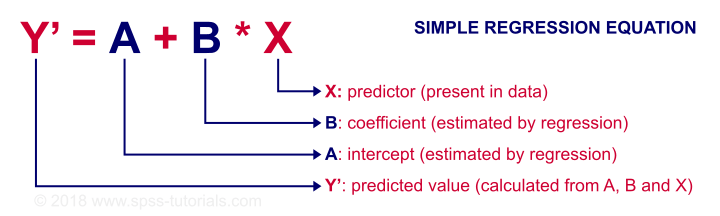
Since X is in our data -in this case, our IQ scores- we can predict performance if we know the intercept (or constant) and the B coefficient. Let's first have SPSS calculate these and then zoom in a bit more on what they mean.

Prediction Formula for Performance

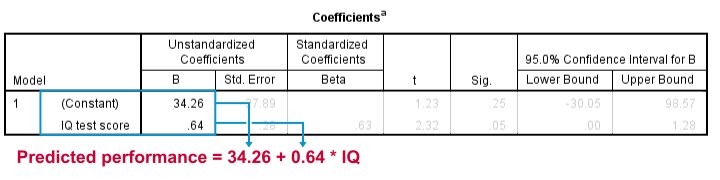
This output tells us that the best possible prediction for job performance given IQ is predicted performance = 34.26 + 0.64 * IQ. So if we get an applicant with an IQ score of 100, our best possible estimate for his performance is predicted performance = 34.26 + 0.64 * 100 = 98.26.

So the core output of our regression analysis are 2 numbers:

• An intercept (constant) of 34.26 and
• a b coefficient of 0.64.

So where did these numbers come from and what do they mean?

B Coefficient - Regression Slope

A b coefficient is number of units increase in Y associated with one unit increase in X. Our b coefficient of 0.64 means that one unit increase in IQ is associated with 0.64 units increase in performance. We visualized this by adding our regression line to our scatterplot as shown below.

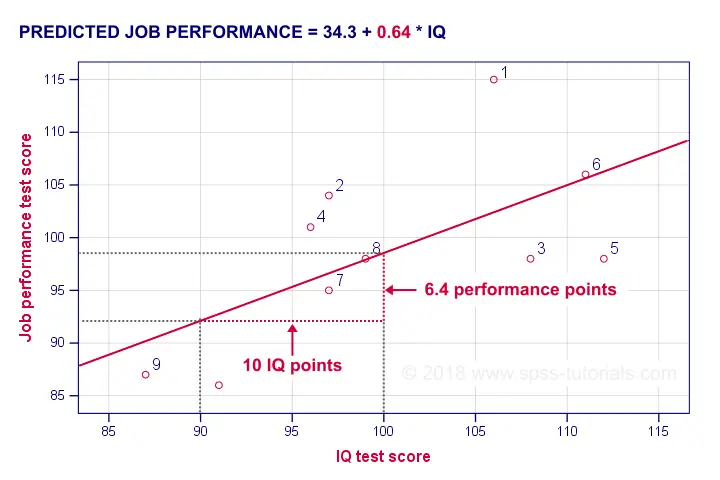
On average, employees with IQ = 100 score 6.4 performance points higher than employees with IQ = 90. The higher our b coefficient, the steeper our regression line. This is why b is sometimes called the regression slope.

Regression Intercept (“Constant”)

The intercept is the predicted outcome for cases who score 0 on the predictor. If somebody would score IQ = 0, we'd predict a performance of (34.26 + 0.64 * 0 =) 34.26 for this person. Technically, the intercept is the y score where the regression line crosses (“intercepts”) the y-axis as shown below.

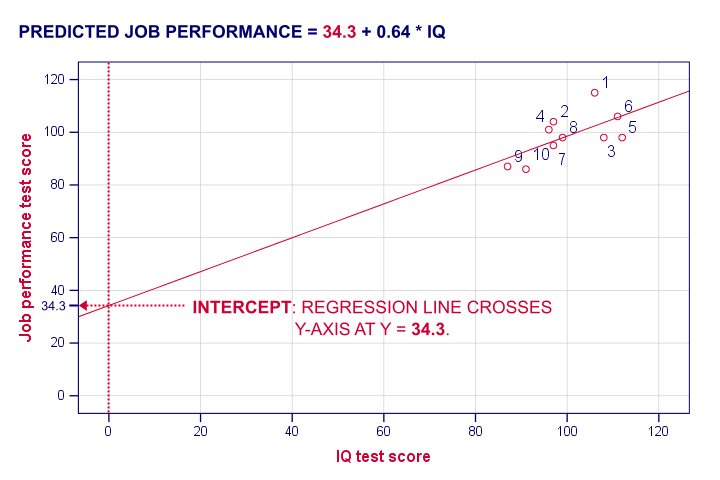
I hope this clarifies what the intercept and b coefficient really mean. But why does SPSS come up with a = 34.3 and b = 0.64 instead of some other numbers? One approach to the answer starts with the regression residuals.

Regression Residuals

A regression residual is the observed value - the predicted value on the outcome variable for some case. The figure below visualizes the regression residuals for our example.

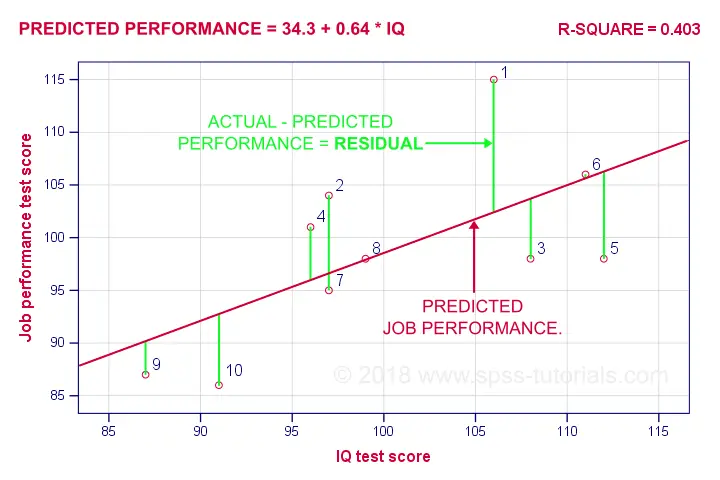
For most employees, their observed performance differs from what our regression analysis predicts. The larger this difference (residual), the worse our model predicts performance for this employee. So how well does our model predict performance for all cases?
Let's first compute the predicted values and residuals for our 10 cases. The screenshot below shows them as 2 new variables in our data. Note that performance = pred + resid.

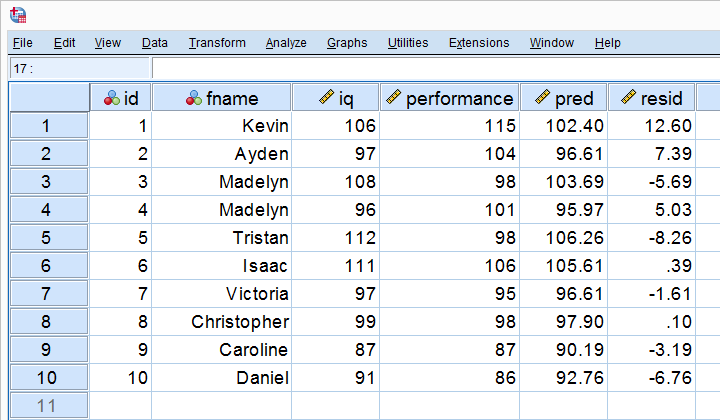
Our residuals indicate how much our regression equation is off for each case. So how much is our regression equation off for all cases? The average residual seems to answer this question. However, it is always zero: positive and negative residuals simply add up to zero. So instead, we compute the mean squared residual which happens to be the variance of the residuals.

Error Variance

Error variance is the mean squared residual and indicates how badly our regression model predicts some outcome variable. That is, error variance is variance in the outcome variable that regression doesn't “explain”. So is error variance a useful measure? Almost. A problem is that the error variance is not a standardized measure: an outcome variable with a large variance will typically result in a large error variance as well. This problem is solved by dividing the error variance by the variance of the outcome variable. Subtracting this from 1 results in r-square.

R-Square - Predictive Accuracy

R-square is the proportion of variance in the outcome variable that's accounted for by regression. One way to calculate it is from the variance of the outcome variable and the error variance as shown below.

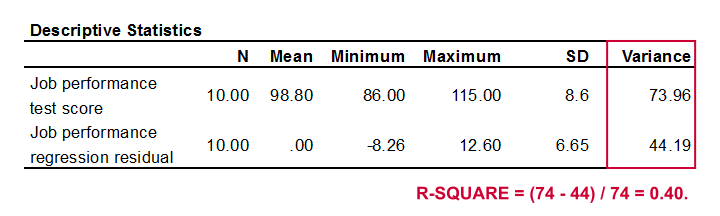
Performance has a variance of 73.96 and our error variance is only 44.19. This means that our regression equation accounts for some 40% of the variance in performance. This number is known as r-square. R-square thus indicates the accuracy of our regression model.
A second way to compute r-square is simply squaring the correlation between the predictor and the outcome variable. In our case, 0.634² = 0.40. It's called r-square because “r” denotes a sample correlation in statistics.

So why did our regression come up with 34.26 and 0.64 instead of some other numbers? Well, that's because regression calculates the coefficients that maximize r-square. For our data, any other intercept or b coefficient will result in a lower r-square than the 0.40 that our analysis achieved.

Inferential Statistics

Thus far, our regression told us 2 important things:

• how to predict performance from IQ: the regression coefficients;
• how well IQ can predict performance: r-square.

Thus far, both outcomes only apply to our 10 employees. If that's all we're after, then we're done. However, we probably want to generalize our sample results to a (much) larger population. Doing so requires some inferential statistics, the first of which is r-square adjusted.

R-Square Adjusted

R-square adjusted is an unbiased estimator of r-square in the population. Regression computes coefficients that maximize r-square for our data. Applying these to other data -such as the entire population- probably results in a somewhat lower r-square: r-square adjusted. This phenomenon is known as shrinkage.

For our data, r-square adjusted is 0.33, which is much lower than our r-square of 0.40. That is, we've quite a lot of shrinkage. Generally,

• smaller sample sizes result in more shrinkage and
• including more predictors (in multiple regression) results in more shrinkage.

Standard Errors and Statistical Significance

Last, let's walk through the last bit of our output.

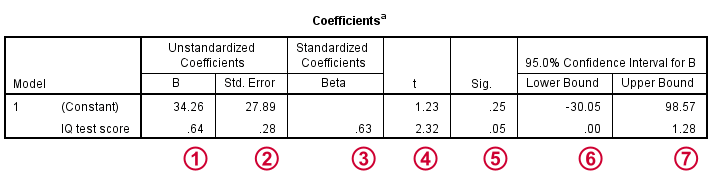
The intercept and b coefficient define the linear relation that best predicts the outcome variable from the predictor.
The standard errors are the standard deviations of our coefficients over (hypothetical) repeated samples. Smaller standard errors indicate more accurate estimates.
Beta coefficients are standardized b coefficients: b coefficients computed after standardizing all predictors and the outcome variable. They are mostly useful for comparing different predictors in multiple regression. In simple regression, beta = r, the sample correlation.
t is our test statistic -not interesting but necessary for computing statistical significance.
“Sig.” denotes the 2-tailed significance for or b coefficient, given the null hypothesis that the population b coefficient is zero.
The 95% confidence interval gives a likely range for the population b coefficient(s).

Thanks for reading!