Measurement levels refer to different types of variables
that imply how to analyze them.
Standard textbooks distinguish 4 such measurement levels or variable types. From low to high, these are
- nominal variables;
- ordinal variables;
- interval variables;
- ratio variables.
The “higher” the measurement level, the more information a variable holds. The simple flowchart below shows how to classify a variable.
Measurement Levels - Classical Approach
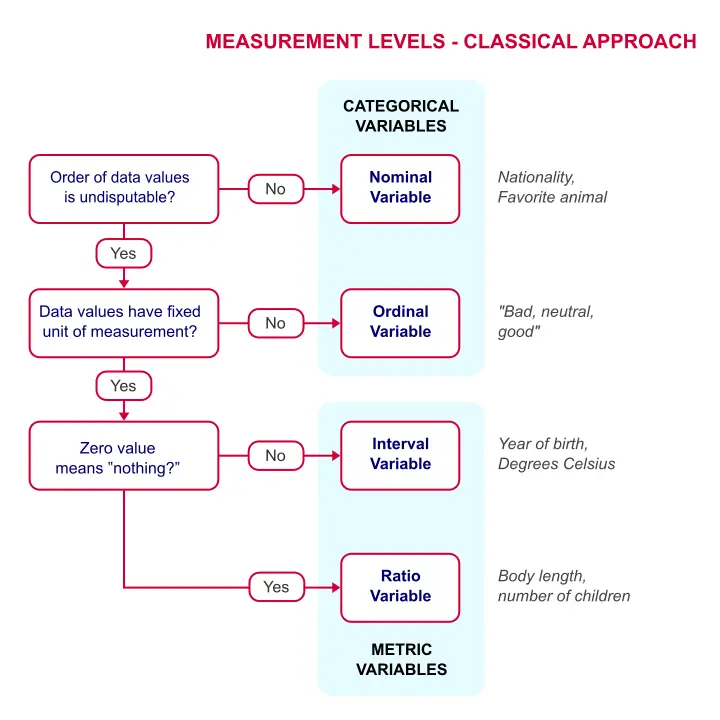 Quick Overview of Measurement Levels
Quick Overview of Measurement Levels
Let's now take a closer look at what these variable types really mean with some examples.
Nominal Variables
A nominal variable is a variable whose
values don't have an undisputable order.
So let's say we asked respondents in which country they live and the answers are
- the Netherlands;
- Belgium;
- France;
- Germany;
- Luxembourg.
So what's the correct order for these countries? Well, we could sort them alphabetically, according to their sizes or to numbers of inhabitants. Different orders make sense for a list of countries. In short,
countries don't have an undisputable order
and therefore “country” is a nominal variable.
Now, countries may be represented by numbers (1 = Netherlands, 2 = Belgium and so on) in SPSS or some other data format. These numbers do have an undisputable order. But country is still a nominal variable because what's represented by these numbers -countries- does not have an undisputable order.
 Country -even if represented as numbers- is still a nominal variable
Country -even if represented as numbers- is still a nominal variable
In a similar vein, ZIP codes -representing geographical areas which don't have a clear order- are nominal as well. But prices in dollars -representing amounts of money- obviously do have an undisputable order and hence are not nominal.
Ordinal Variables
Ordinal variables hold values that have an undisputable order
but no fixed unit of measurement.
Some fixed units of measurement are meters, people, dollars or seconds. However, there's no fixed unit of measurement for a question like
“how did you like your food?”
with the following answer categories:
- Bad;
- Neutral;
- Good.
Some may argue that Bad = 1 point, Neutral = 2 points and Good = 3 points. But that's just a wild guess. Perhaps our respondents feel Neutral represents 1.5 or 2.5 points. This is illustrated by the figure below.
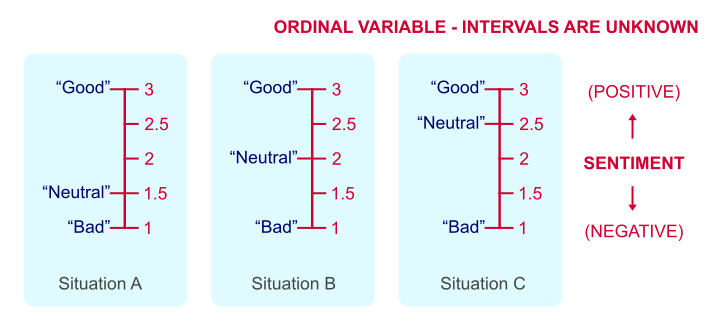 Intervals between answer categories are unknown for ordinal variables.
Intervals between answer categories are unknown for ordinal variables.
We've no way to prove which scenario is true because just “points” are not a fixed unit of measurement. And since we don't know if Neutral represents 1.5, 2 or 2.5 points, calculations on ordinal variables are not meaningful. Less strictly though, calculations on ordinal variables are quite common under the Assumption of Equal Intervals.
Also note that monthly income measured as
- Less than € 1000,-;
- € 1000,- to € 2000,-;
- € 2000,- or over.
is ordinal. Euros are a fixed unit of measurement but the answers are income categories, not numbers of Euros.
Interval Variables
Interval variables have a fixed unit of measurement
but zero does not mean “nothing”.
One of the rare examples is “in which year did it happen?”
Ignoring leap days, years are a fixed unit of measurement for time. However, the year zero doesn't mean “nothing” with regard to time.
As a consequence,
multiplication is not meaningful for interval variables.
The year 2000 isn't “twice as late” as the year 1000. The same goes for temperature in degrees Celsius: zero degrees is not “nothing” with regard to temperature. Therefore, 100 degrees is not twice as hot as 50 degrees. This argument could, however, be made for temperature in Kelvin.
We should add that these are the only 2 examples of interval variables we could think of. Interval variables are always analyzed similarly to ratio variables -which we'll turn to next. But distinguishing these as separate measurement levels -all textbooks still do- is pointless.
Ratio Variables
Ratio variables have a fixed unit of measurement
and zero really means “nothing.”
An example is weight in kilos. A kilo is a fixed unit of measurement because it always represents the exact same weight. Also, zero kilos corresponds to “nothing” with regard to weight. As a consequence,
multiplication is meaningful for ratio variables.
In fact, we don't need more than a kitchen scale to prove that 2 times 1 kilo really is the same amount of weight as 1 time 2 kilos.
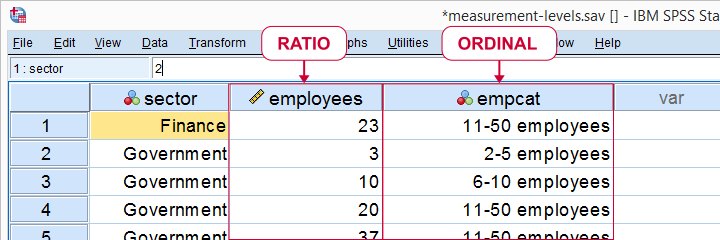 Number of employees as ratio as well as ordinal variable
Number of employees as ratio as well as ordinal variable
Some text books mention an “absolute zero point”. We rather avoid this phrasing because ratio variables may hold negative values; the balance of my bank account may be negative but is has a fixed unit of measurement -Euros in my case- and zero means “nothing”.
Classical Measurement Levels - Shortcomings
We argued that measurement levels matter because they facilitate data analysis. However, when we look at common statistical techniques, we see that
- dichotomous variables are treated differently from all other variables but classical measurement levels fail to distinguish them;
- metric variables (interval and ratio) are always treated identically;
- categorical variables (nominal and ordinal) are sometimes treated similarly and sometimes not.
Because of these reasons, we think the classification below is much more helpful.
Measurement Levels - Modern Approach
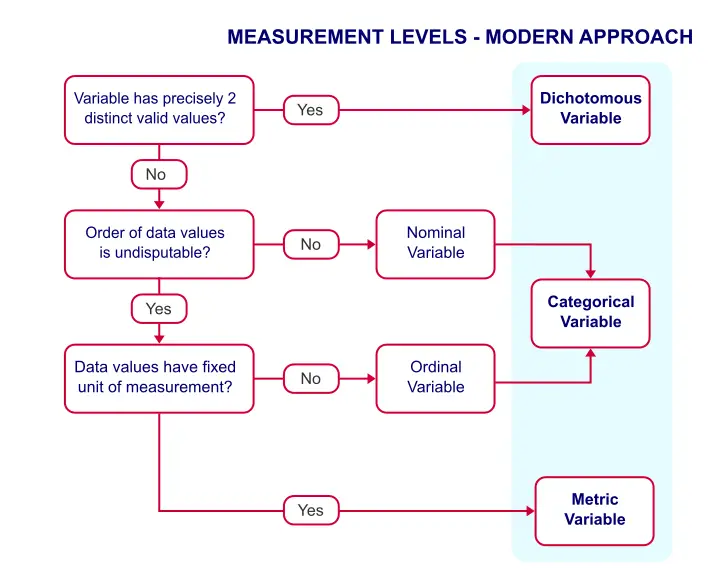
This classification distinguishes 3 main categories which we'll briefly discuss.
Dichotomous Variables
Dichotomous variables have precisely two distinct values. Typical examples are sex, owning a car or carrying HIV. It is useful to distinguish dichotomous variables as a separate measurement level because they require different analyses than other variables:
- an independent samples t-test tests if a dichotomous variable is associated with a metric variable;
- a z-test and Phi-coefficient are used to test if 2 dichotomous variables are associated;
- logistic regression predicts a dichotomous outcome variable.
Categorical Variables
Categorical variables are variables on which
calculations are not meaningful.
Therefore, nominal and ordinal variables are categorical variables. They contain (usually few) answer categories. Because calculations are not meaningful, categorical variables merely define groups. We therefore analyze them with frequency distributions and bar charts.
Metric Variables
Metric variables are variables on which
calculations are meaningful.
That is: interval and ratio variables are metric variables. Because calculations are allowed, we typically analyze them with descriptive statistics such as
- means;
- standard deviations;
- skewnesses.
Data Analysis - Next Steps
We just argued that
- categorical variables define groups of cases and
- we use descriptive statistics for analyzing metric variables.
Now, say we'd like to know if 2 categorical variables are associated. Then the first variable defines groups and the second variable defines groups within those groups. A table that shows just that is a contingency table as shown below. It basically holds frequency distributions within frequency distributions
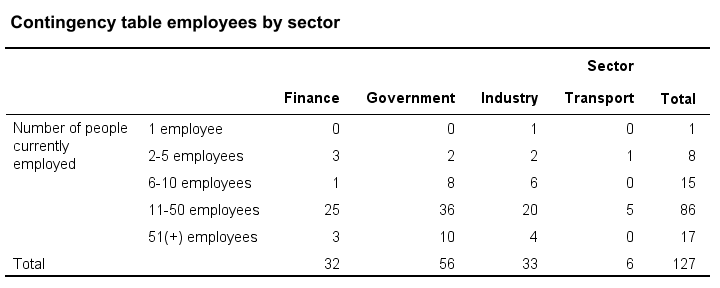
Next, we could visualize the association with a stacked bar chart. Or we may test if the association is statistically significant by running a chi-square independence test on our contingency table.
Or perhaps we'd like to know if a categorical variable and a metric variable are associated. The categorical variable defines groups. Within those groups, we'll inspect descriptive statistics over our metric variable. We thus arrive at the table as shown below.
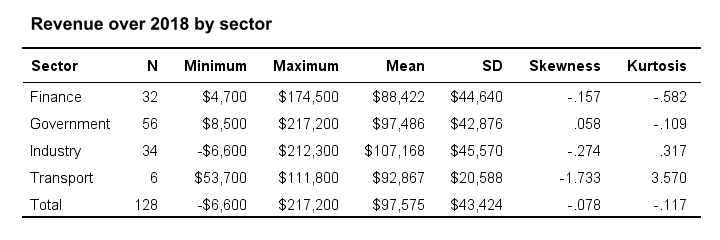
We could visualize the means as a bar chart for means by category. Or we could test if the population means differ by category with ANOVA.
So now we see how measurement levels help us choose the right analyses. For a more complete overview of analyses by measurement level, see SPSS Data Analysis - Basic Roadmap.
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 38 COMMENTS:
By lukwago umar on October 21st, 2016
interesting but being my first time am still confused if you can reccomend me for books i can read in my free time its better. send them via my email thanks
By Jon Peck on March 27th, 2017
Thanks for contributing to this rather confusing topic. There are a few places to go next.
- the variable role. Measurement level has a different impact depending on how a variable will be used, e.g., as a predictor in regression, in a tree analysis, or in, say, t tests and in graphics and tables.
- Calculating with combinations of variables. It may be perfectly okay to multiply a dichotomous variable by another type depending on the coding but not appropriate to add them.
We once considered trying to assign a measurement level to a computed quantity but decided that it was too hard to get this right in the general case.
- Simple addition might not be okay even with interval or ratio variables depending on the units.
As you doubtless know, Statistics can attempt to guess the measurement level for a variable if it is unknown. This happens both in Data > Define Variable Properties and in more recent versions when the data are passed, but it can certainly be fooled. The heuristics use the number and type of values, the variable format, and other properties to guess. The user can, of course, override this.
By Jon Peck on March 29th, 2017
The site says "This Tutorial has 11 Comments", but I can only see the first. Maybe that means that the others have not been approved.
By Ruben Geert van den Berg on March 29th, 2017
I know, the CMS is not entirely tidy. I was confident nobody would notice or care about the wrong comment count but I didn't take you into account ;-) Ok, I'll fix it.
By Eileen Potter on June 9th, 2017
Lovely, clear discussion. Percentages are my problem and I have been bounced around with 'ordinal', 'ratio' and 'interval' explanations. Metric would be so much more useful.