An assumption required for ANOVA is homogeneity of variances. We often run Levene’s test to check if this holds. But what if it doesn't? This tutorial walks you through.
- SPSS ANOVA Dialogs I
- Results I - Levene’s Test “Significant“
- SPSS ANOVA Dialogs II
- Results II - Welch and Games-Howell Tests
- Plan B - Kruskal-Wallis Test
Example Data
All analyses in this tutorial use staff.sav, part of which is shown below. We encourage you to download these data and replicate our analyses.
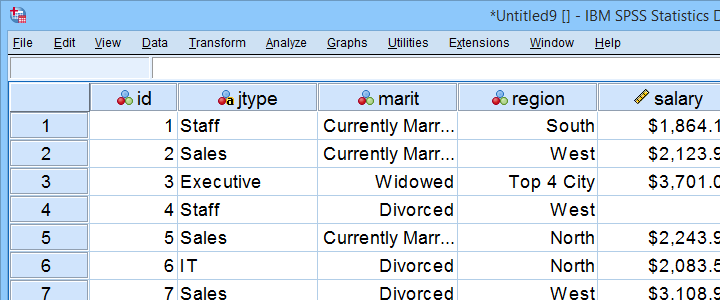
Our data contain some details on a sample of N = 179 employees. The research question for today is: is salary associated with region? We'll try to support this claim by rejecting the null hypothesis that all regions have equal mean population salaries. A likely analysis for this is an ANOVA but this requires a couple of assumptions.
ANOVA Assumptions
An ANOVA requires 3 assumptions:
- independent observations;
- normality: the dependent variable must follow a normal distribution within each subpopulation.
- homogeneity: the variance of the dependent variable must be equal over all subpopulations.
With regard to our data, independent observations seem plausible: each record represents a distinct person and people didn't interact in any way that's likely to affect their answers.
Second, normality is only needed for small sample sizes of, say, N < 25 per subgroup. We'll inspect if our data meet this requirement in a minute.
Last, homogeneity is only needed if sample sizes are sharply unequal. If so, we usually run Levene's test. This procedure tests if 2+ population variances are all likely to be equal.
Quick Data Check
Before running our ANOVA, let's first see if the reported salaries are even plausible. The best way to do so is inspecting a histogram which we'll create by running the syntax below.
frequencies salary
/format notable
/histogram.
Result
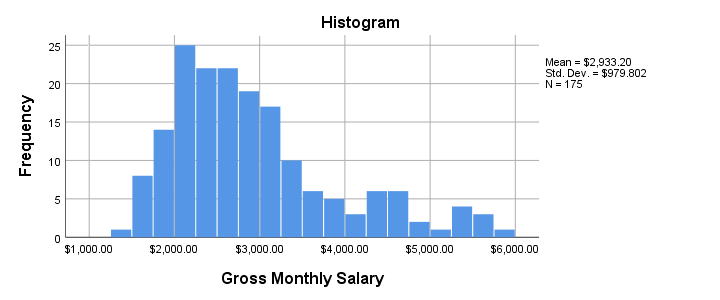
- Note that our histogram reports N = 175 rather than our N = 179 respondents. This implies that salary contains 4 missing values.
- The frequency distribution, however, looks plausible: there's no clear outliers or other abnormalities that should ring any alarm bells.
- The distribution shows some positive skewness. However, this makes perfect sense and is no cause for concern.
Let's now proceed to the actual ANOVA.
SPSS ANOVA Dialogs I
After opening our data in SPSS, let's first navigate to

 as shown below.
as shown below.
Let's now fill in the dialog that opens as shown below.
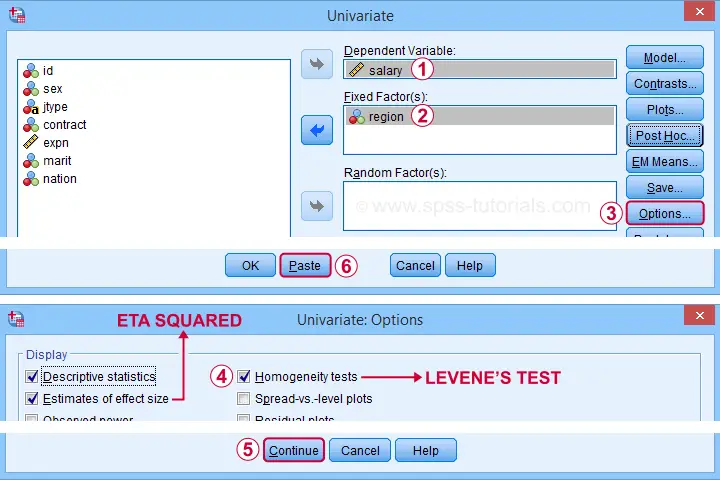
Completing these steps results in the syntax below. Let's run it.
UNIANOVA salary BY region
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT ETASQ DESCRIPTIVE HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=region.
Results I - Levene’s Test “Significant”
The very first thing we inspect are the sample sizes used for our ANOVA and Levene’s test as shown below.
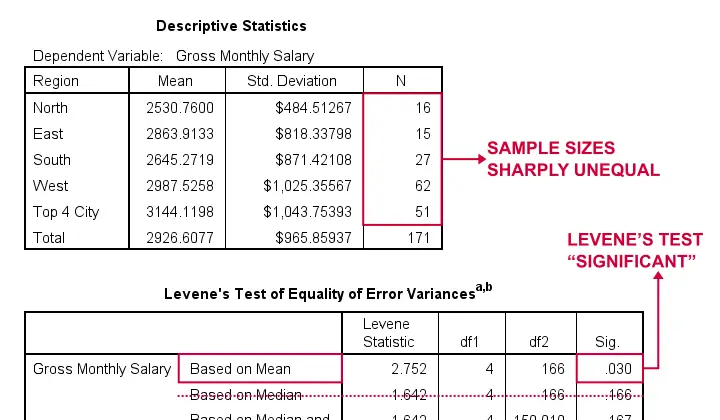
- First off, note that our Descriptive Statistics table is based on N = 171 respondents (bottom row). This is due to some missing values in both region and salary.
- Second, sample sizes for “North” and “East” are rather small. We may therefore need the normality assumption. For now, let's just assume it's met.
- Next, our sample sizes are sharply unequal so we really need to meet the homogeneity of variances assumption.
- However, Levene’s test is statistically significant because its p < 0.05: we reject its null hypothesis of equal population variances.
The combination of these last 2 points implies that we can not interpret or report the F-test shown in the table below.
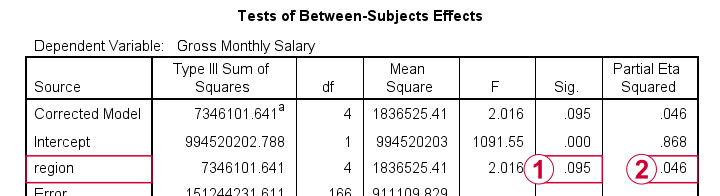
 As discussed, we can't rely on this p-value for the usual F-test.
As discussed, we can't rely on this p-value for the usual F-test.
 However, we can still interpret eta squared (often written as η2). This is a descriptive statistic that neither requires normality nor homogeneity. η2 = 0.046 implies a small to medium effect size for our ANOVA.
However, we can still interpret eta squared (often written as η2). This is a descriptive statistic that neither requires normality nor homogeneity. η2 = 0.046 implies a small to medium effect size for our ANOVA.
Now, if we can't interpret our F-test, then how can we know if our mean salaries differ? Two good alternatives are:
- running an ANOVA with the Welch statistic or
- a Kruskal-Wallis test.
Let's start off with the Welch statistic.
SPSS ANOVA Dialogs II
For inspecting the Welch statistic, first navigate to

 as shown below.
as shown below.
Next, we'll fill out the dialogs that open as shown below.
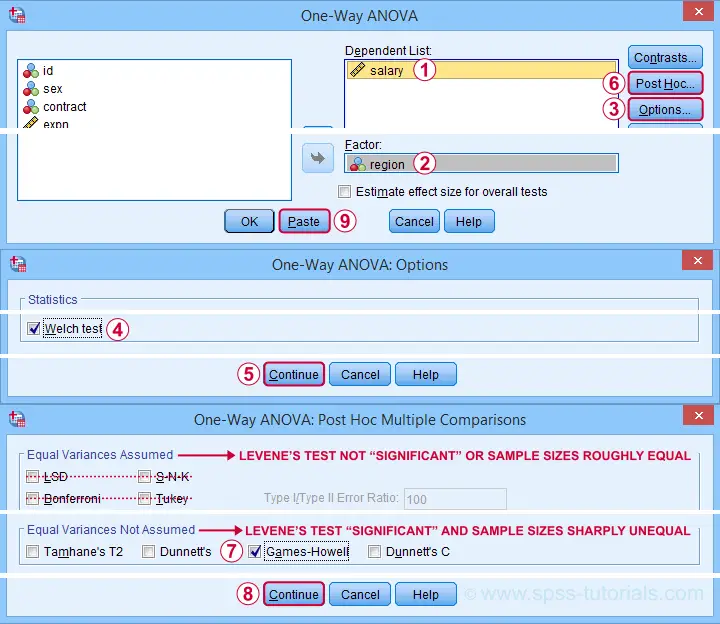
This results in the syntax below. Again, let's run it.
ONEWAY salary BY region
/STATISTICS HOMOGENEITY WELCH
/MISSING ANALYSIS
/POSTHOC=GH ALPHA(0.05).
Results II - Welch and Games-Howell Tests
As shown below, the Welch test rejects the null hypothesis of equal population means.

This table is labelled “Robust Tests...” because it's robust to a violation of the homogeneity assumption as indicated by Levene’s test. So we now conclude that mean salaries are not equal over all regions.
But precisely which regions differ with regard to mean salaries? This is answered by inspecting post hoc tests. And if the homogeneity assumption is violated, we usually prefer Games-Howell as shown below.
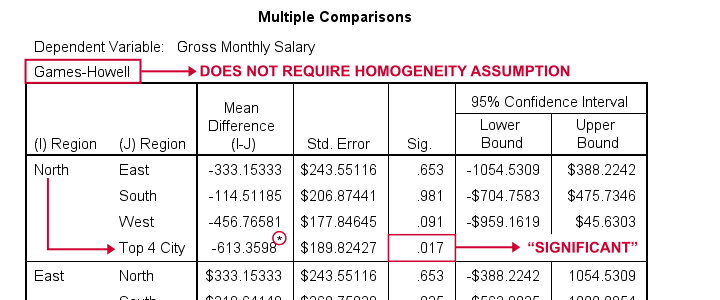
Note that each comparison is shown twice in this table. The only regions whose mean salaries differ “significantly” are North and Top 4 City.
Plan B - Kruskal-Wallis Test
So far, we overlooked one issue: some regions have sample sizes of n = 15 or n = 16. This implies that the normality assumption should be met as well. A terrible idea here is to run
for each region separately. Neither test rejects the null hypothesis of a normally distributed dependent variable but this is merely due to insufficient sample sizes.
A much better idea is running a Kruskal-Wallis test. You could do so with the syntax below.
NPAR TESTS
/K-W=salary BY region(1 5)
/STATISTICS DESCRIPTIVES
/MISSING ANALYSIS.
Result

Sadly, our Kruskal-Wallis test doesn't detect any difference between mean salary ranks over regions, H(4) = 6.58, p = 0.16.
In short, our analyses come up with inconclusive outcomes and it's unclear precisely why. If you've any suggestions, please throw us a comment below. Other than that,
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 13 COMMENTS:
By Jon K Peck on August 8th, 2022
First, region 5 is described as "Top 4 City", which seems rather different from all the others, so it might be wise to exclude it in this analysis. That's homogeneity of definition rather than homogeneity of variance :-) (The unknown region eq 6 cases would be automatically excluded).
Second, in sizing up the data, it would be better to look at a graphic that takes the region into account. If you do a scatter of salary vs region (a boxplot would work better for a larger sample), it is immediately obvious by the IOT (intra-ocular test) that the variances are very different for the groups.
While the formal test is, well, more formal, one could conclude without even doing the homogeneity test that the homogeneity of variance assumption is seriously violated. Since the magnitudes of the data are not very different across the groups, a variance-stabilizing transformation, which would often be considered in situations like this, is probably not going to help much here.
So, I think you just have to bite the bullet and analyze the data without the equal-variance assumption. Sticking with the Games-Howell test, which as you say does not require that assumption, you get a good picture of the results. The post-hoc shows that groups 1, 2, and 3 do not differ from each other at all. The sig levels for the pairwise comparisons are all huge. However, 1 vs 4 is borderline significant (.06). Welch and Brown-Forsythe also show that none of the differences are significant, but the post-hoc tests are more informative.
So I think the appropriate statistical conclusion is that means do not differ among the first three regions, but there is some evidence that region 4 is different, at least from region 1. If you get the spread vs level plot that is available with Univariate, you get another view of how the means and variances are related.
By Ruben Geert van den Berg on August 9th, 2022
Hi Jon!
I agree with your suggestions. The only point I'm missing is an argument against starting off with the Welch test here.
I feel it's unusual to run post hoc tests such as GH or BF without even looking at some omnibus test first, right?
P.s. I don't necessarily agree with this last point: several (roughly) equal means may obscure a substantial difference with one or two groups in an onmibus test (but not in post hoc tests).
By Jon K Peck on August 9th, 2022
The key thing about post hoc tests is that, with the exception of LSD, they control the familywise error rate to account for multiple testing, (LSD is the exception in that it is just the equivalent of doing all the individual t tests).
They don't depend on the ANOVA results. The advice generally given is to only do a post hoc test if the overall ANOVA F is significant, but since the tests do control the overall error rate, it's a little strange to require a significant F first.
The logic is that the post hoc confirms what the significant F arises from, but the math doesn't depend on that. Of course, the appropriate procedure does depend on the hypothesis in question.
This page has a discussion of the issue.
https://stats.stackexchange.com/questions/9751/do-we-need-a-global-test-before-post-hoc-tests
Quoting just one part, "...I'll add some quotes from Maxwell and Delaney (2004): "...these methods [e.g., Bonferroni, Tukey, Dunnet, etc.] should be viewed as substitutes for the omnibus test because they control alphaEW at the desired level all by themselves.
Requiring a significant omnibus test before proceeding to perform any of these analyses, as is sometimes done, only serves to lower alphaEW below the desired level (Bernhardson, 1975) and hence inappropriately decreases power" (p. 236)."
By Ruben Geert van den Berg on August 10th, 2022
Yes, that's basically my opinion as well: why require a "significant" omnibus test if post hoc tests are already designed to control the family-wise error rates for multiple tests?
Sadly, I don't see this point of view in many text books.
But -honestly- I'm not a fan of post hoc tests in the first place. IMHO, statistical significance is very much overrated compared to CI's and effect sizes.
By YY on August 11th, 2022
Besides the tests of normality, the detrended Q-Q plots showed obvious and serious non-normality, especially for the last three groups.
I tried the reciprocal square root transformation on the response variable.
The residuals (from the transformed data) became more normally distributed and more homogeneous in variances.
Both the overall F test and the Tukey test got insignificant results with the transformed data.