For reading up on some basics, see ANOVA - What Is It?

• One-Way ANOVA - Null Hypothesis
• ANOVA Assumptions
• SPSS ANOVA Flowchart
• SPSS One-Way ANOVA Dialog
• SPSS ANOVA Output
• ANOVA - APA Reporting Guidelines

ANOVA Example - Effect of Fertilizers on Plants

A farmer wants to know which fertilizer is best for his parsley plants. So he tries different fertilizers on different plants and weighs these plants after 6 weeks. The data -partly shown below- are in parsley.sav.

Quick Data Check - Split Histograms

After opening our data in SPSS, let's first see what they basically look like. A quick way for doing so is inspecting a histogram of weights for each fertilizer separately. The screenshot below guides you through.

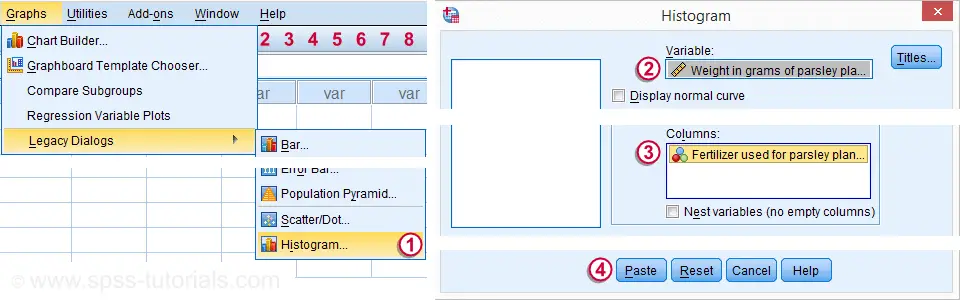
After following these steps, clicking Paste results in the syntax below. Let's run it.

Result

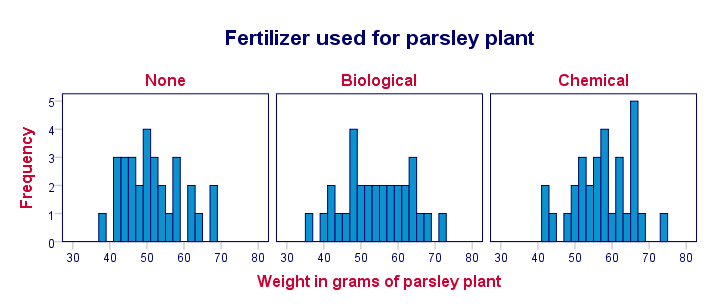
Importantly, these distributions look plausible and we don't see any outliers: our data seem correct to begin with -not always the case with real-world data!
Conclusion: the vast majority of weights are between some 40 and 65 grams and they seem reasonably normally distributed.

Inspecting Sample Sizes and Means

Precisely how did the fertilizers affect the plants? Let's compare some descriptive statistics for fertilizers separately. The quickest way is using MEANS which we could paste from Analyze Compare Means Means but just typing the syntax may be just as easy.

Result

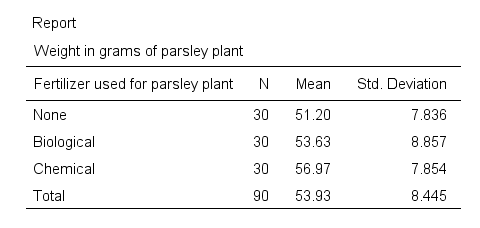
• We have sample sizes of n = 30 for each fertilizer.
• Second, the chemical fertilizer resulted in the highest mean weight of almost 57 grams. “None” performed worst at some 51 grams while “Biological” is in between.
• “Biological” has a slightly higher standard deviation than the other conditions but the difference is pretty small.

Now, this table tells us a lot about our samples of plants. But what do our sample means say about the population means? Can we say anything about the effects of fertilizers on all (future) plants? We'll try to do so by refuting the statement that all fertilizers perform equally: our null hypothesis.

One-Way ANOVA - Null Hypothesis

The null hypothesis for ANOVA is that all population means are equal. If this is true, then our sample means will probably differ a bit anyway. However, very different sample means contradict the hypothesis that the population means are equal. In this case, we may conclude that this null hypothesis probably wasn't true after all.
ANOVA will basically tells us to what extent our null hypothesis is credible. However, it requires some assumptions regarding our data.

ANOVA Assumptions

• independent observations: each record in the data must be a distinct and independent entity.Precisely, the assumption is “independent and identically distributed variables” but a thorough explanation is way beyond the scope of this tutorial.
• normality: the dependent variable is normally distributed in the population. Normality is not needed for reasonable sample sizes, say each n ≥ 25.
• homogeneity: the variance of the dependent variable must be equal in each subpopulation. Homogeneity is only needed for (sharply) unequal sample sizes. In this case, Levene's test can be used to see if homogeneity is met.

So how to check if we meet these assumptions? And what to do if we violate them? The simple flowchart below guides us through.

SPSS ANOVA Flowchart

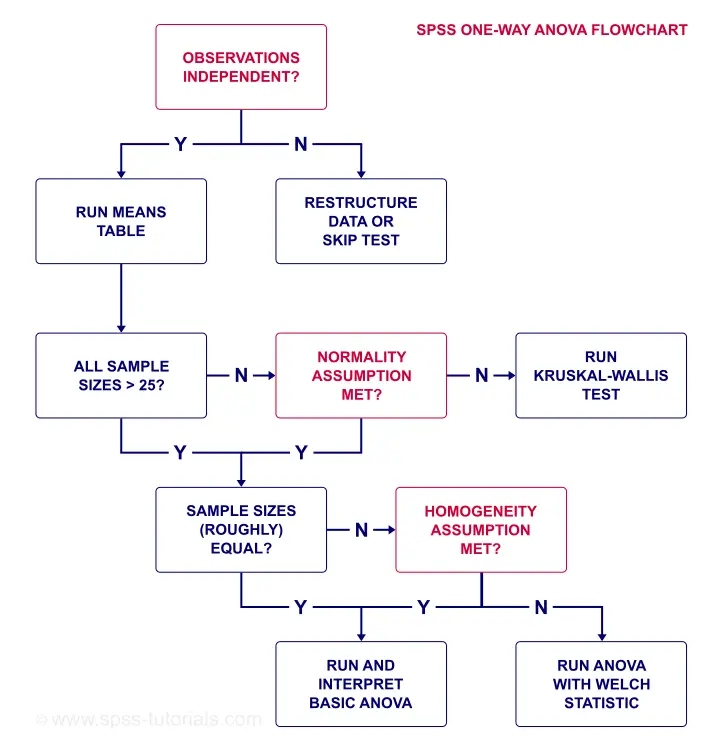
So what about our data?

• Our plants seem to be independent observations: each has a different id value (first variable).
• Our means table shows that each n ≥ 25 so we don't need to meet normality.
• Since our sample sizes are equal, we don't need the homogeneity assumption either.

So why do we inspect our sample sizes based on a means table? Why didn't we just look at the frequency distribution for fertilizer? Well, our ANOVA uses only cases without missing values on our dependent variable. And our means table shows precisely those.
A second reason is that we need to report the means and standard deviations per group. And the means table gives us precisely the statistics we want in the order we want them.

SPSS One-Way ANOVA Dialog

We'll now run a basic ANOVA from the menu. The screenshot below guides you through.

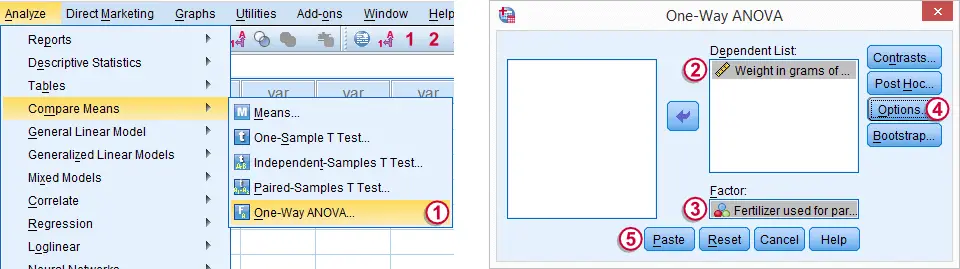
The Paste button creates the syntax below.

One-Way ANOVA Syntax

SPSS One-Way ANOVA Output

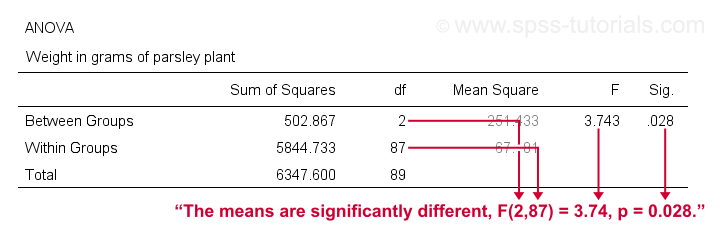
A general rule of thumb is that we reject the null hypothesis if “Sig.” or p < 0.05 which is the case here. So we reject the null hypothesis that all population means are equal.
Conclusion: different fertilizers perform differently. The differences between our mean weights -ranging from 51 to 57 grams- are statistically significant.

ANOVA - APA Reporting Guidelines

First and foremost, we'll report our means table. Regarding the significance test, the APA suggests we report

• the F value;
• df1, the numerator degrees of freedom;
• df2, the denominator degrees of freedom;
• the p value

like so: “our three fertilizer conditions resulted in different mean weights for the parsley plants, F(2,87) = 3.7, p = .028.”

One-Way ANOVA - Next Steps

For this example, there's 2 more things we could take a look at:

• Post hoc tests: our ANOVA results tell us that not all population means are equal. But precisely which mean differs from which other mean? This is answered by running post hoc tests. For an outstanding tutorial, consult SPSS - One Way ANOVA with Post Hoc Tests Example.
• Effect size: we concluded that fertilizers affect mean weights but how strong is this effect? A common effect size measure for ANOVA is partial eta squared. Sadly, effect size is absent from the One-Way dialog.
  Oddly, MEANS does include eta-squared but lacks other essential options such as Levene’s test. For complete output, you need to run your ANOVA twice from 2 different commands. This really is a major stupidity in SPSS. There. I said it.

ANOVA with Eta-Squared from MEANS

Result

Right, so that's about the most basic SPSS ANOVA tutorial I could come up with. I hope you found it helpful. Let me know what you think by throwing me a comment below.

Thanks for reading!