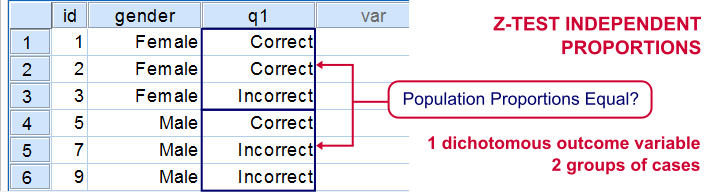
If you'd like to know if 2 groups of people score similarly on 1 dichotomous variable, you'll compare 2 independent proportions. There's two basic ways to do so:
- the chi-square independence test and;
- the z-test for 2 independent proportions.
These tests yield identical p-values but the z-test approach allows you to compute a confidence interval for the difference between the proportions. Unfortunately, this very basic test is painfully absent from SPSS. We'll therefore present a freely downloadable tool for it in the remainder of this tutorial.
Installation
- This tool requires SPSS version 18 or higher with the SPSS Python Essentials properly installed and tested.
- Download the Confidence Intervals Independent Proportions tool.
- For SPSS versions 18 through 22, select

 . For SPSS 24, select
. For SPSS 24, select  .
.
Navigate to the confidence intervals extension (its file name ends in “.spe”, short for SPSS Extension) and install it. - Although you'll get a popup that the extension was successfully installed, it'll only work after you close and reopen SPSS entirely (unless you're on version 24).
- You'll now find the tool under
 .
.
Operations
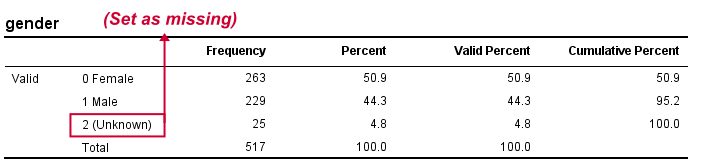
- Make sure the grouping variable has exactly two valid values. If this doesn't hold, the tool will throw a fatal error pointing out the problem.
- The grouping variable may be a numeric variable or a string variable. If it's a string, keep in mind that empty string values are valid by default in SPSS but you can specify them as user missing values.
- The test variables must have exactly two valid values as well. Variables violating this requirement will be skipped when calculating results.
- The test variables may be any mixture of numeric and string variables.
- The p-values and confidence intervals are based on the normal distribution. This approximation is sufficiently accurate if p1*n1, (1-p1)*n1, p2*n2 and (1-p2)*n2 are all > 5, where p and n denote the two test proportions and their related sample sizes.1 If this does not hold, a warning will be added to the results.
- If any SPLIT FILE is in effect, the tool will switch if off, throw a warning that it did so and then proceed as usual.
- If a WEIGHT variable is in effect, results will be based on rounded frequencies. P-values may be biased if you're using non integer sampling weights but this holds for all p-values in SPSS except for those from the complex samples module.2,3,4
Example
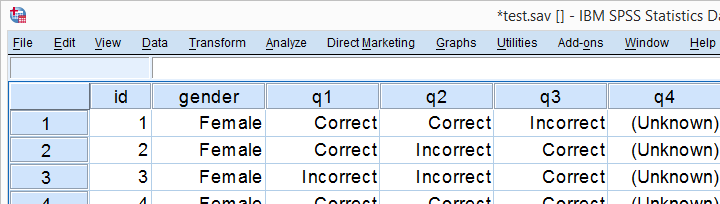
Let's just try things out on test.sav, part of which is shown below. We'll test if men and women score differently on separate items.
Data Inspection
We'll first see if we need to specify any user missing values by running the syntax below.
set tnumbers both.
*See if all variables have exactly two valid values.
frequencies gender to passes.
*Set missing values as needed. The tiny mistake here of omitting q5 is deliberate.
missing values gender to q4 (2).
*Show only value labels in output.
set tnumbers labels.
Result
Crosstabs
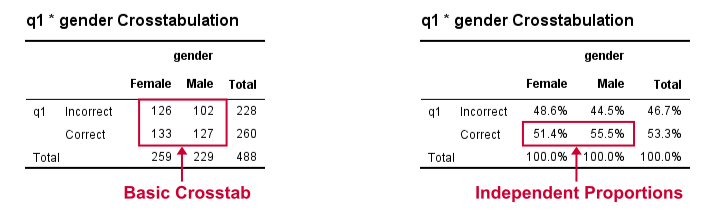
We'll now run some super basic CROSSTABS. We'll normally skip this step but for now they'll help us understand the results from our tool that we'll see in a minute.
crosstabs q1 by gender.
*Independent proportions.
crosstabs q1 by gender/cells column.
Result
Computing our Confidence Intervals
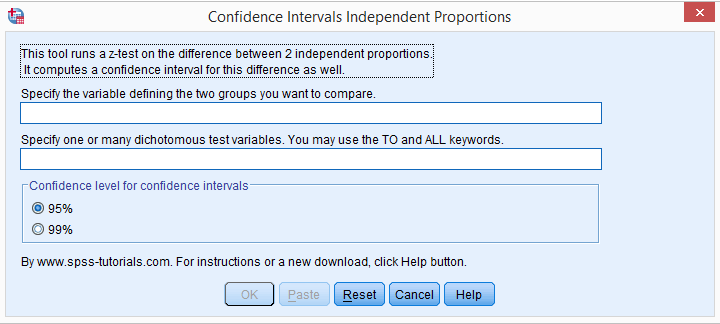
We'll select  and fill out the main dialog as below.
and fill out the main dialog as below.
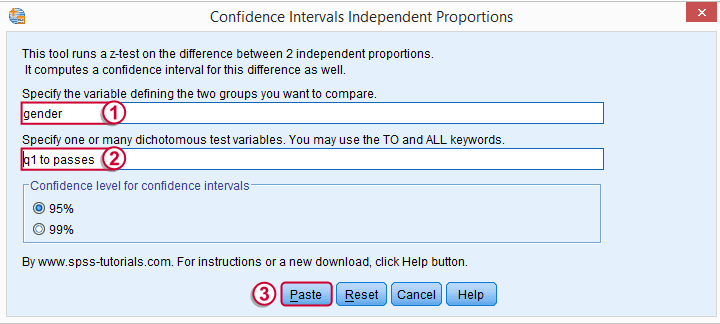
 Note that TO may be used for a range of variable names.
Note that TO may be used for a range of variable names.
 Clicking results in the syntax below.
Clicking results in the syntax below.
CONFIDENCE_INTERVALS_INDEPENDENT_PROPORTIONS GROUP = 'gender' VARIABLES = 'q1 to passes' LEVEL = 95.
Results
Upon running our syntax, a new dataset will pop up holding both crosstabs we saw earlier for each test variable. Note that most variables have variable labels explaining their precise meaning. You can see them in variable view or hover over a variable’s name in data view as shown in the screenshot below.

The crosstab with frequencies holds the input data for our calculations. The crosstab with percentages (screenshot below) holds our test proportions. Each test variable results in 2 rows, one for each value. You'll typically need just one but the setup chosen here makes the interface efficient and flexible.
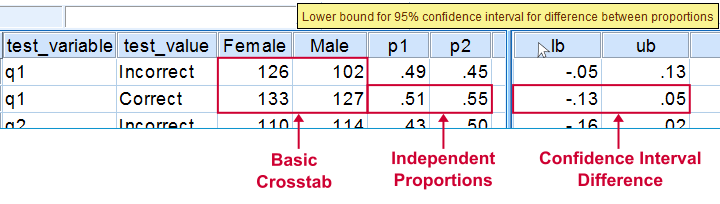
Further right we find our z-test. Its p-value indicates the probability of finding the observed difference between our independent proportions if the population difference is zero. The p-values are identical of those yielded by Pearson’s chi-square in CROSSTABS.
We then encounter our confidence intervals. Last but not least, we may or may not have some notes (in this case we do).
That's it. I hope you'll find this tool useful. Please let me know by leaving a comment. Thank you!
References
- Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [Statistics, part 3]. Amsterdam: Boom.
- Fowler, F.J. (2009). Survey Research Methods. Thousand Oaks, CA: SAGE.
- De Leeuw, E.D., Hox, J.J. and Dillman, D.A. (2008). International Handbook of Survey Methodology. New York: Lawrence Erlbaum Associates.
- Kish, L. Weighting for Unequal Pi. Journal of Official Statistics, 8, 183-200.
 SPSS TUTORIALS
SPSS TUTORIALS
THIS TUTORIAL HAS 2 COMMENTS:
By Stephen Barlow on August 19th, 2017
Dear Sir
very helpful, would you have link for other extension macros? need other test's as well.
By Ruben Geert van den Berg on August 19th, 2017
Hi Stephen!
I also built confidence intervals for Pearson correlations: http://www.spss-tutorials.com/spss-confidence-intervals-for-correlations-tool/
And confidence intervals for a single proportion: http://www.spss-tutorials.com/z-test-and-confidence-interval-proportion-tool/
I don't have any other statistical tests built as extensions (not macros btw) but I'm planning to build some online tools. Honestly, these won't come up any time soon I expect.