Effect size is an interpretable number that quantifies
the difference between data and some hypothesis.
Statistical significance is roughly the probability of finding your data if some hypothesis is true. If this probability is low, then this hypothesis probably wasn't true after all. This may be a nice first step, but what we really need to know is how much do the data differ from the hypothesis? An effect size measure summarizes the answer in a single, interpretable number. This is important because
- effect sizes allow us to compare effects -both within and across studies;
- we need an effect size measure to estimate (1 - β) or power. This is the probability of rejecting some null hypothesis given some alternative hypothesis;
- even before collecting any data, effect sizes tell us which sample sizes we need to obtain a given level of power -often 0.80.
Overview Effect Size Measures
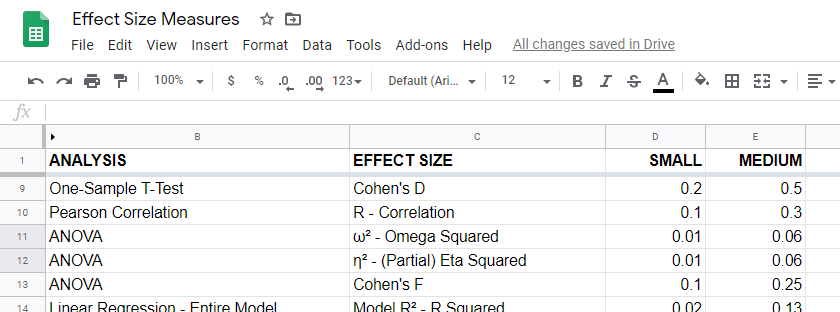
For an overview of effect size measures, please consult this Googlesheet shown below. This Googlesheet is read-only but can be downloaded and shared as Excel for sorting, filtering and editing.
Chi-Square Tests
Common effect size measures for chi-square tests are
- Cohen’s W (both chi-square tests);
- Cramér’s V (chi-square independence test) and
- the contingency coefficient (chi-square independence test) .
Chi-Square Tests - Cohen’s W
Cohen’s W is the effect size measure of choice for
Basic rules of thumb for Cohen’s W8 are
- small effect: w = 0.10;
- medium effect: w = 0.30;
- large effect: w = 0.50.
Cohen’s W is computed as
$$W = \sqrt{\sum_{i = 1}^m\frac{(P_{oi} - P_{ei})^2}{P_{ei}}}$$
where
- \(P_{oi}\) denotes observed proportions and
- \(P_{ei}\) denotes expected proportions under the null hypothesis for
- \(m\) cells.
For contingency tables, Cohen’s W can also be computed from the contingency coefficient \(C\) as
$$W = \sqrt{\frac{C^2}{1 - C^2}}$$
A third option for contingency tables is to compute Cohen’s W from Cramér’s V as
$$W = V \sqrt{d_{min} - 1}$$
where
- \(V\) denotes Cramér's V and
- \(d_{min}\) denotes the smallest table dimension -either the number of rows or columns.
Cohen’s W is not available from any statistical packages we know. For contingency tables, we recommend computing it from the aforementioned contingency coefficient.
For chi-square goodness-of-fit tests for frequency distributions your best option is probably to compute it manually in some spreadsheet editor. An example calculation is presented in this Googlesheet.
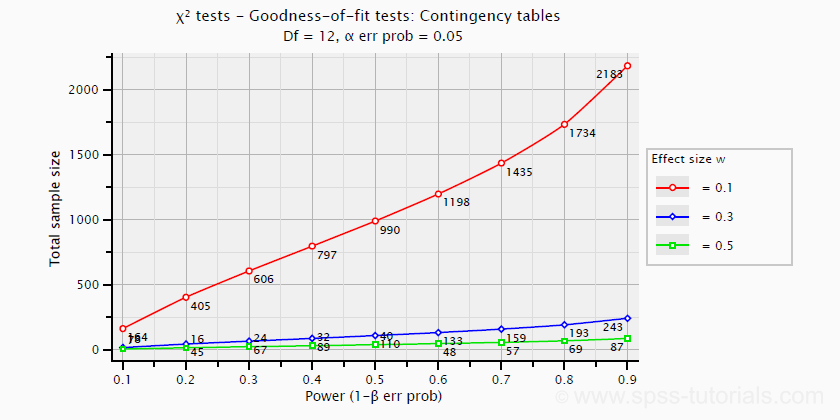
Power and required sample sizes for chi-square tests can't be directly computed from Cohen’s W: they depend on the df -short for degrees of freedom- for the test. The example chart below applies to a 5 · 4 table, hence df = (5 - 1) · (4 -1) = 12.
T-Tests
Common effect size measures for t-tests are
- Cohen’s D (all t-tests) and
- the point-biserial correlation (only independent samples t-test).
T-Tests - Cohen’s D
Cohen’s D is the effect size measure of choice for all 3 t-tests:
- the independent samples t-test,
- the paired samples t-test and
- the one sample t-test.
Basic rules of thumb are that8
- |d| = 0.20 indicates a small effect;
- |d| = 0.50 indicates a medium effect;
- |d| = 0.80 indicates a large effect.
For an independent-samples t-test, Cohen’s D is computed as
$$D = \frac{M_1 - M_2}{S_p}$$
where
- \(M_1\) and \(M_2\) denote the sample means for groups 1 and 2 and
- \(S_p\) denotes the pooled estimated population standard deviation.
A paired-samples t-test is technically a one-sample t-test on difference scores. For this test, Cohen’s D is computed as
$$D = \frac{M - \mu_0}{S}$$
where
- \(M\) denotes the sample mean,
- \(\mu_0\) denotes the hypothesized population mean (difference) and
- \(S\) denotes the estimated population standard deviation.
Cohen’s D is present in JASP as well as SPSS (version 27 onwards). For a thorough tutorial, please consult Cohen’s D - Effect Size for T-Tests.
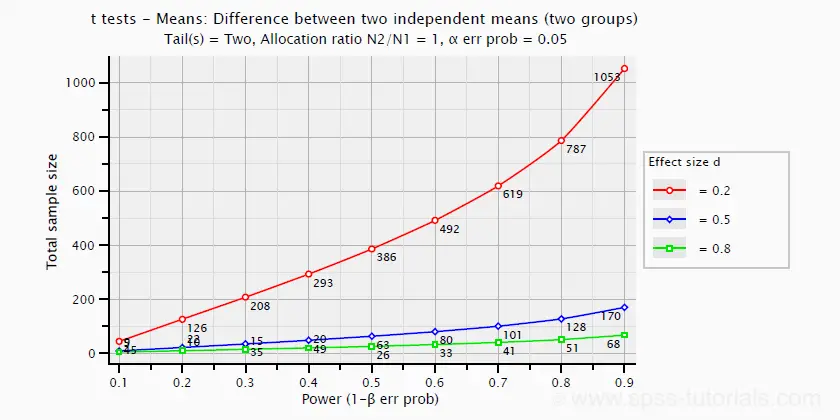
The chart below shows how power and required total sample size are related to Cohen’s D. It applies to an independent-samples t-test where both sample sizes are equal.
Pearson Correlations
For a Pearson correlation, the correlation itself (often denoted as r) is interpretable as an effect size measure. Basic rules of thumb are that8
- r = 0.10 indicates a small effect;
- r = 0.30 indicates a medium effect;
- r = 0.50 indicates a large effect.
Pearson correlations are available from all statistical packages and spreadsheet editors including Excel and Google sheets.
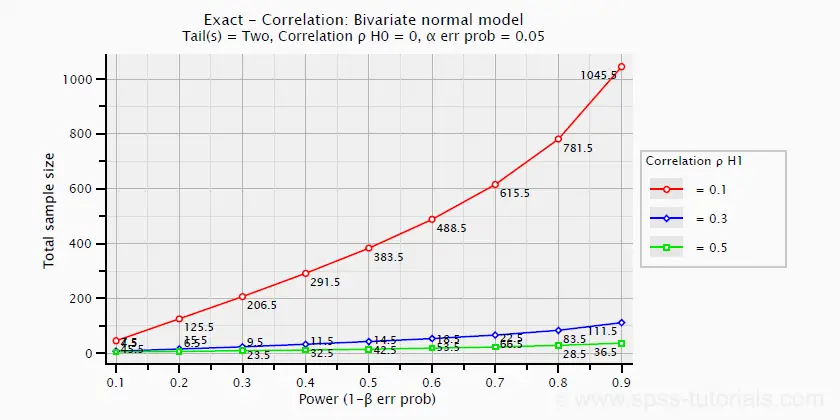
The chart below -created in G*Power- shows how required sample size and power are related to effect size.
ANOVA
Common effect size measures for ANOVA are
- \(\color{#0a93cd}{\eta^2}\) or (partial) eta squared;
- Cohen’s F;
- \(\color{#0a93cd}{\omega^2}\) or omega-squared.
ANOVA - (Partial) Eta Squared
Partial eta squared -denoted as η2- is the effect size of choice for
- ANOVA (between-subjects, one-way or factorial);
- repeated measures ANOVA (one-way or factorial);
- mixed ANOVA.
Basic rules of thumb are that
- η2 = 0.01 indicates a small effect;
- η2 = 0.06 indicates a medium effect;
- η2 = 0.14 indicates a large effect.
Partial eta squared is calculated as
$$\eta^2_p = \frac{SS_{effect}}{SS_{effect} + SS_{error}}$$
where
- \(\eta^2_p\) denotes partial eta-squared and
- \(SS\) denotes effect and error sums of squares.
This formula also applies to one-way ANOVA, in which case partial eta squared is equal to eta squared.
Partial eta squared is available in all statistical packages we know, including JASP and SPSS. For the latter, see How to Get (Partial) Eta Squared from SPSS?
ANOVA - Cohen’s F
Cohen’s f is an effect size measure for
- ANOVA (between-subjects, one-way or factorial);
- repeated measures ANOVA (one-way or factorial);
- mixed ANOVA.
Cohen’s f is computed as
$$f = \sqrt{\frac{\eta^2_p}{1 - \eta^2_p}}$$
where \(\eta^2_p\) denotes (partial) eta-squared.
Basic rules of thumb for Cohen’s f are that8
- f = 0.10 indicates a small effect;
- f = 0.25 indicates a medium effect;
- f = 0.40 indicates a large effect.
G*Power computes Cohen’s f from various other measures. We're not aware of any other software packages that compute Cohen’s f.
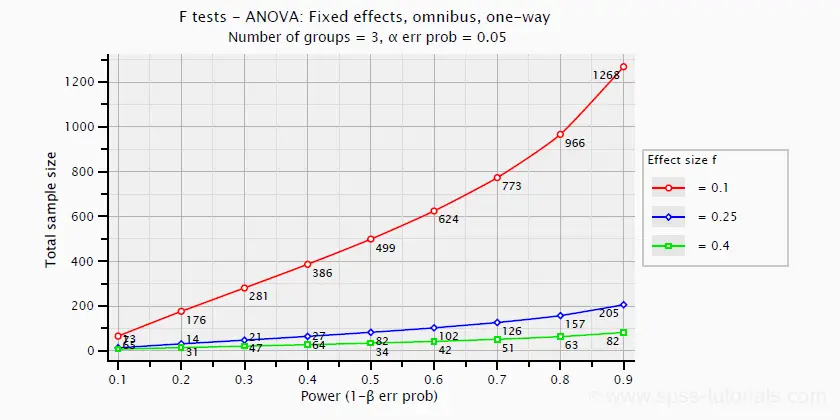
Power and required sample sizes for ANOVA can be computed from Cohen’s f and some other parameters. The example chart below shows how required sample size relates to power for small, medium and large effect sizes. It applies to a one-way ANOVA on 3 equally large groups.
ANOVA - Omega Squared
A less common but better alternative for (partial) eta-squared is \(\omega^2\) or Omega squared computed as
$$\omega^2 = \frac{SS_{effect} - df_{effect}\cdot MS_{error}}{SS_{total} + MS_{error}}$$
where
- \(SS\) denotes sums of squares;
- \(df\) denotes degrees of freedom;
- \(MS\) denotes mean squares.
Similarly to (partial) eta squared, \(\omega^2\) estimates which proportion of variance in the outcome variable is accounted for by an effect in the entire population. The latter, however, is a less biased estimator.1,2,6 Basic rules of thumb are5
- Small effect: ω2 = 0.01;
- Medium effect: ω2 = 0.06;
- Large effect: ω2 = 0.14.
\(\omega^2\) is available in SPSS version 27 onwards but only if you run your ANOVA from The other ANOVA options in SPSS (via General Linear Model or Means) do not yet include \(\omega^2\). However, it's also calculated pretty easily by copying a standard ANOVA table into Excel and entering the formula(s) manually.
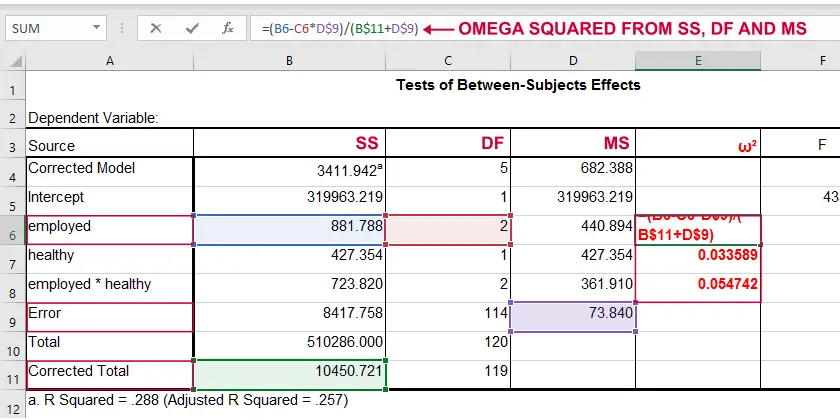 Note: you need “Corrected total” for computing omega-squared from SPSS output.
Note: you need “Corrected total” for computing omega-squared from SPSS output.
Linear Regression
Effect size measures for (simple and multiple) linear regression are
- \(\color{#0a93cd}{f^2}\) (entire model and individual predictor);
- \(R^2\) (entire model);
- \(r_{part}^2\) -squared semipartial (or “part”) correlation (individual predictor).
Linear Regression - F-Squared
The effect size measure of choice for (simple and multiple) linear regression is \(f^2\). Basic rules of thumb are that8
- \(f^2\) = 0.02 indicates a small effect;
- \(f^2\) = 0.15 indicates a medium effect;
- \(f^2\) = 0.35 indicates a large effect.
\(f^2\) is calculated as
$$f^2 = \frac{R_{inc}^2}{1 - R_{inc}^2}$$
where \(R_{inc}^2\) denotes the increase in r-square for a set of predictors over another set of predictors. Both an entire multiple regression model and an individual predictor are special cases of this general formula.
For an entire model, \(R_{inc}^2\) is the r-square increase for the predictors in the model over an empty set of predictors. Without any predictors, we estimate the grand mean of the dependent variable for each observation and we have \(R^2 = 0\). In this case, \(R_{inc}^2 = R^2_{model} - 0 = R^2_{model}\) -the “normal” r-square for a multiple regression model.
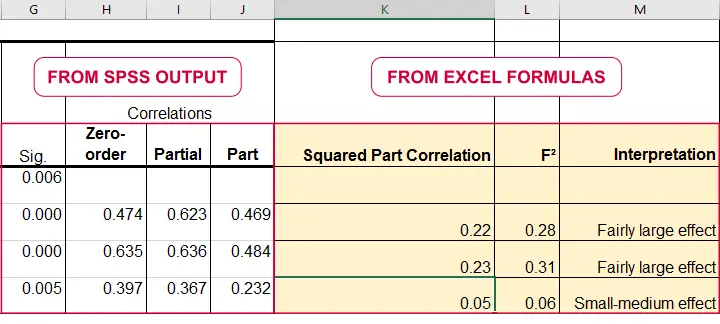
For an individual predictor, \(R_{inc}^2\) is the r-square increase resulting from adding this predictor to the other predictor(s) already in the model. It is equal to \(r^2_{part}\) -the squared semipartial (or “part”) correlation for some predictor. This makes it very easy to compute \(f^2\) for individual predictors in Excel as shown below.
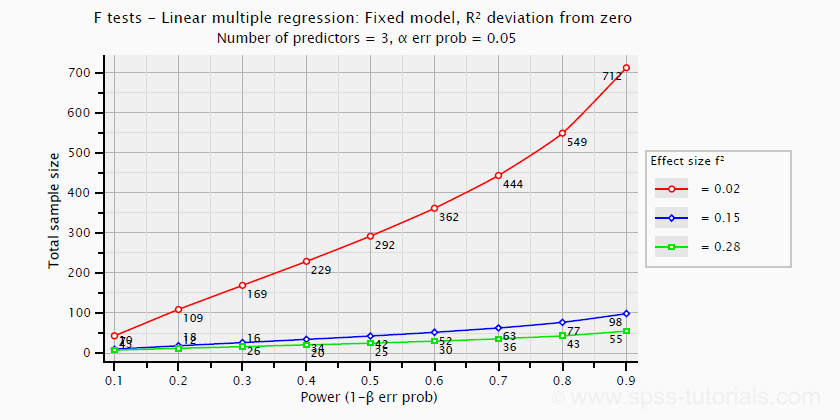
\(f^2\) is useful for computing the power and/or required sample size for a regression model or individual predictor. However, these also depend on the number of predictors involved. The figure below shows how required sample size depends on required power and estimated (population) effect size for a multiple regression model with 3 predictors.
Right, I think that should do for now. We deliberately limited this tutorial to the most important effect size measures in a (perhaps futile) attempt to not overwhelm our readers. If we missed something crucial, please throw us a comment below. Other than that,
thanks for reading!
References
- Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [Statistics, part 3]. Amsterdam: Boom.
- Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.
- Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
- Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
- Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
- Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
- Siegel, S. & Castellan, N.J. (1989). Nonparametric Statistics for the Behavioral Sciences (2nd ed.). Singapore: McGraw-Hill.
- Cohen, J (1988). Statistical Power Analysis for the Social Sciences (2nd. Edition). Hillsdale, New Jersey, Lawrence Erlbaum Associates.
- Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition). New York: Routledge.
 SPSS TUTORIALS
SPSS TUTORIALS

THIS TUTORIAL HAS 18 COMMENTS:
By Jon K Peck on July 4th, 2022
Cohen d and several variations on it are available in SPSS Statistics as part of the t test output.
Two variants of omega squared are available from the anova procedures.
By Ruben Geert van den Berg on July 5th, 2022
Hi Jon, you're totally right, shame on me! Failed to send the updated version to the DB...
Btw, am I right that there's no effect size for individual predictors in logistic regression?
I'm aware of EXP(B) but this is just as scale dependent as B itself: changing a variable from dollars to dollar cents affects it. Doing so does not affect beta coefficients in linear regression.
So for logistic regression with predictors on different scales, how can I compare their relative strengths?
Am I missing something here?
By Jon K Peck on July 5th, 2022
It's true that the two logistic regression procedures don't provide effect estimates, but it seems to me that the coefficients or exponentiated terms speak for themselves,
and standardizing the variables removes the effect of measurement units.
.
Here's an article that speaks to logistic specifically.
https://www.theanalysisfactor.com/effect-size-statistics-logistic-regression/