SPSS RM ANOVA – 2 Within-Subjects Factors
- Repeated Measures ANOVA - Null Hypothesis
- Repeated Measures ANOVA - Assumptions
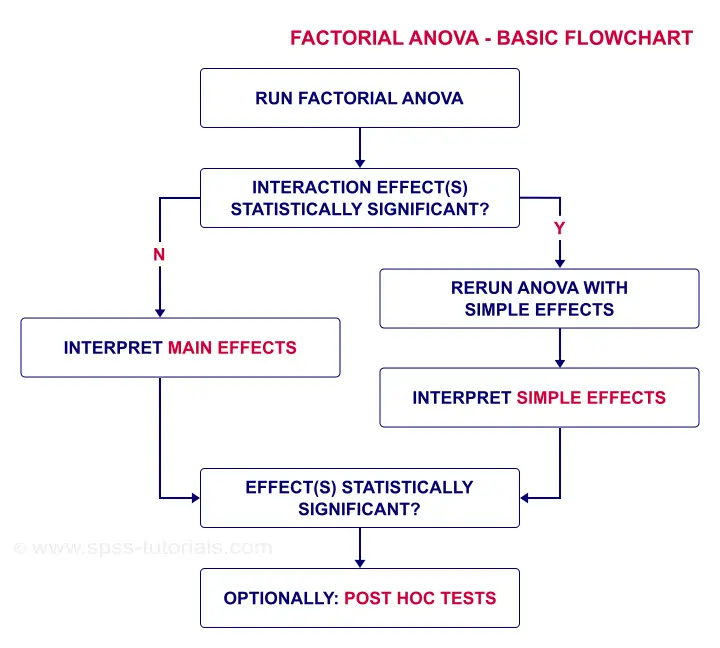
- Factorial ANOVA - Basic Flowchart
- Factorial Repeated Measures ANOVA in SPSS
- Repeated Measures ANOVA - APA Style Reporting
How does alcohol consumption affect driving performance? A study tested 36 participants during 3 conditions:
- no alcohol - 0 glasses of beer;
- medium alcohol - 2 glasses of beer;
- high alcohol - 4 glasses of beer.
Each participant went through all 3 conditions in random order on 3 consecutive days. During each condition, the participants drove for 30 minutes in a driving simulator. During these “rides” they were confronted with 5 trials: dangerous situations to which they need to respond fast. The 15 reaction times (5 trials for each of 3 conditions) are in alcoholtest.sav, part of which is shown below.
The main research questions are
- how does alcohol affect reaction times?
- how does trial affect reaction times?
- does the effect of alcohol depend on trial?
We'll obviously inspect the mean reaction times over (combinations of) conditions and trials. However, we've only 36 participants. Based on this tiny sample, what -if anything- can we conclude about the general population? The right way to answer that is running a repeated measures ANOVA over our 15 reaction time variables.
Repeated Measures ANOVA - Null Hypothesis
Generally, the null hypothesis for a repeated measures ANOVA is that
the population means of 3+ variables are all equal.
If this is true, then the corresponding sample means may differ somewhat. However, very different sample means are unlikely if population means are equal. So if that happens, we no longer believe that the population means were truly equal: we reject this null hypothesis.
Now, with 2 factors -condition and trial- our means may be affected by condition, trial or the combination of condition and trial: an interaction effect. We'll examine each of these possible effect separately. This means we'll test 3 null hypotheses:
- population means are equal over conditions;
- population means are equal over trials;
- population means are equal over combinations of condition and trial.
As we're about to see: we may or may not reject each of our 3 hypotheses independently of the others.
Repeated Measures ANOVA - Assumptions
A repeated measures ANOVA will usually run just fine in SPSS. However, we can only trust the results if we meet some assumptions. These are:
- Independent observations or -precisely- independent and identically distributed variables.
- Normality: the test variables follow a multivariate normal distribution in the population. This is only needed for small sample sizes of N < 25 or so. You can test if variables are normally distributed with a Kolmogorov-Smirnov test or a Shapiro-Wilk test.
- Sphericity: the population variances of all difference scores among the test variables must be equal. Sphericity is often tested with Mauchly’s test.
With regard to our example data in alcoholtest.sav:
- Independent observations is probably met: each case contains a separate person who didn't interact in any way with any other participants.
- We don't need normality because we've a reasonable sample size of N = 36.
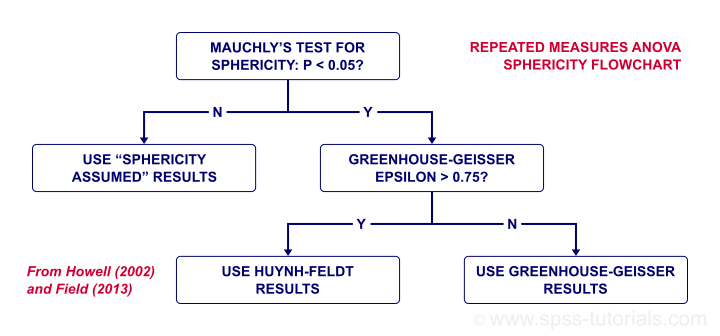
- We'll use Mauchly's test to see if sphericity is met. If it isn't, we'll apply a correction to our results as shown in our sphericity flowchart.
Data Checks I - Histograms
Let's first see if our data look plausible in the first place. Since our 15 reaction times are quantitative variables, running some basic histograms over them will give us some quick insights. The fastest way to do so is running the syntax below. Easier -but slower- alternatives are covered in Creating Histograms in SPSS.
frequencies no_1 to hi_5
/format notable
/histogram.
I won't bother you with the output. See for yourself that all frequency distributions look at least reasonably plausible.
Data Checks II - Missing Values
In SPSS, repeated measures ANOVA uses
only cases without any missing values
on any of the test variables. That's right: cases having one or more missing values on the 15 reaction times are completely excluded from the analysis. This is a major pitfall and it's hard to detect after running the analysis.
Our advice is to
inspect how many cases are complete on all test variables
before running the actual analysis. A very fast way to do so is running a minimal DESCRIPTIVES table.
descriptives no_1 to hi_5.
Result
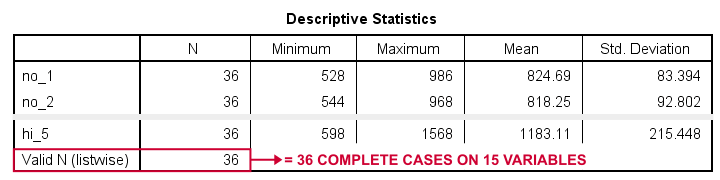
“Valid N (listwise)” indicates the number of cases who are complete on all variables in this table. For our example data, all 36 cases are complete. All cases will be used for our repeated measures ANOVA.
If missing values do occur in other data, you may want to exclude such cases altogether before proceeding. The simplest options are FILTER or SELECT IF. Alternatively, you could try and impute some -or all- missing values.
Creating a Reporting Table
Our last step before the actual ANOVA is creating a table with descriptive statistics for reporting. The APA suggests using 1 row per variable that includes something like
- sample size;
- mean;
- 95% confidence interval for the mean;
- median;
- standard deviation and
- skewness.
A minimal EXAMINE table comes close:
examine no_1 to hi_5.
Sadly, there's some issues with EXAMINE that you must know:
- by default, EXAMINE uses only cases that are complete on all variables in the table. We usually don't want that. However, for this example it's great because our final ANOVA is also restricted to complete cases.
- EXAMINE only reports sample sizes in a separate table. This is utter stupidity. However, for this example it's ok: we know we've 36 complete cases. We'll report this in the table title.
- EXAMINE creates way more output than you need and you can't choose which statistics you'll get in which order. The least cumbersome solution is editing the table in Excel.
After creating the table, we'll rearrange its dimensions like we did in SPSS Correlations in APA Format. The result is shown below.
Reporting Table - Result
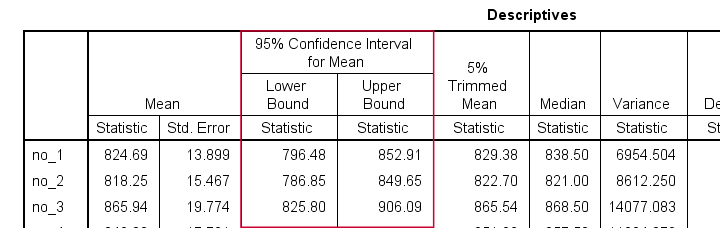
This table contains all descriptives we'd like to report. Moreover, it also allows us to double-check some of the later ANOVA output.
Factorial ANOVA - Basic Flowchart
Factorial Repeated Measures ANOVA in SPSS
The screenshots below guide you through running the actual ANOVA. Note that you'll only have in your menu if you're licensed for the Advanced Statistics module.
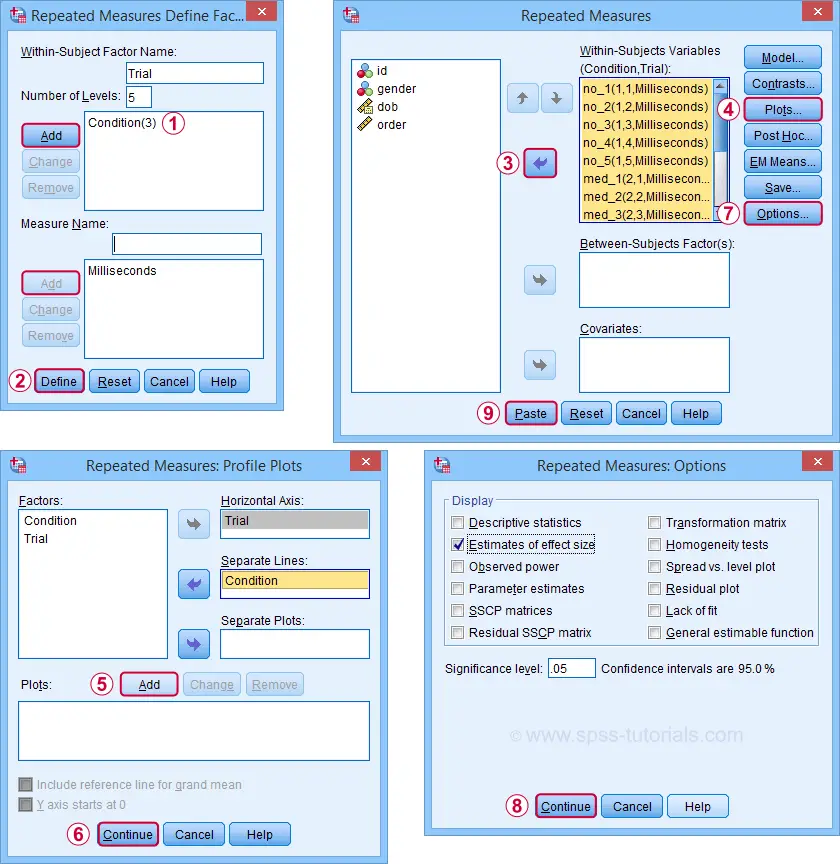
Completing these steps results in the syntax below. Let's run it.
GLM no_1 med_1 hi_1
/WSFACTOR=Condition_1 3 Polynomial
/MEASURE=Milliseconds
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(Condition_1) COMPARE ADJ(BONFERRONI)
/PRINT=ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=Condition_1.
ANOVA Results I - Mauchly's Test
As indicated by our flowchart, we first inspect the interaction effect: condition by trial. Before looking up its significance level, let's first see if sphericity holds for this effect. We find this in the “Mauchly's Test of Sphericity” table shown below.
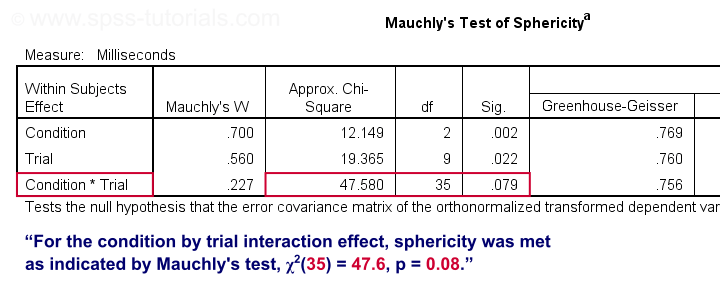
As a rule of thumb, we reject the null hypothesis if p < 0.05. For the interaction effect, “Sig.” or p = 0.079. We retain the null hypothesis. For Mauchly's test, the null hypothesis is that sphericity holds. Conclusion: the sphericity assumption seems to be met. Let's now see if the interaction effect is statistically significant.
ANOVA Results II - Within-Subjects Effects
In the Tests of Within-Subjects Effects table, each effect has 4 rows. We just saw that sphericity holds for the condition by trial interaction. We therefore only use the rows labeled “Sphericity Assumed” as shown below.
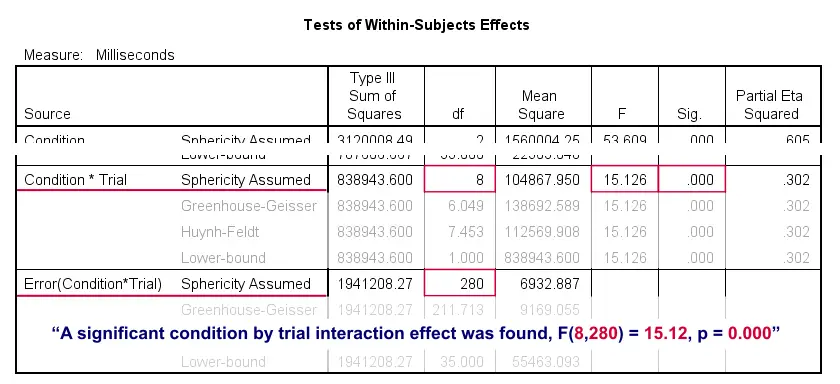
First off, “Sig.” or p = 0.000: the interaction effect is extremely statistically significant. Also note that its effect size -partial eta squared- is 0.302. This indicates a strong effect for condition by trial. But what does that mean? The best way to find out is inspecting our profile plot.
ANOVA Results III - Profile Plot
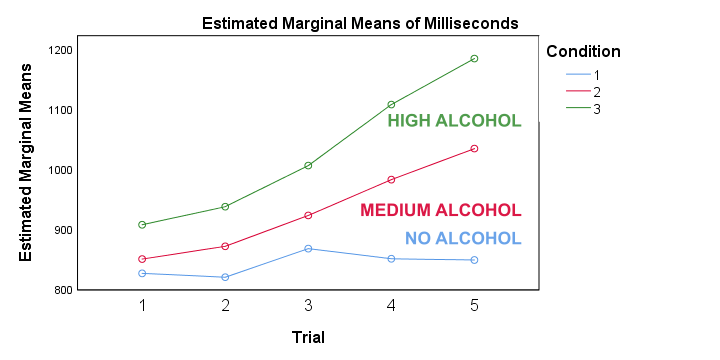
First off, the “estimated marginal means” are simply the observed sample means when running the full factorial model -the default in SPSS. If you're not sure, you can verify this from the reporting table we created earlier. Anyway, what we see is that
- reaction times don't clearly increase over trials for the no alcohol condition;
- reaction times somewhat increase over trials after medium alcohol consumption and
- reaction times strongly increase in the high alcohol condition.
In short, the interaction effect means that the effect of alcohol depends on trial. For the first trial, the lines -representing alcohol conditions- lie close together. But over trials, they diverge further and further. The largest effect of alcohol is seen for trial 5: the reaction times run from 850 milliseconds (no alcohol) up to some 1,200 milliseconds (high alcohol). This implies that there's no such thing as the effect of alcohol. It depends on which trial we inspect. So the logical thing to do is analyze the effect of alcohol for each trial separately. Precisely this is meant by the simple effects suggested in our flowchart.
Rerunning the ANOVA with Simple Effects
So how to run simple effects? It really is simple: we run a one-way repeated measures ANOVA over the 3 conditions for trial 1 only. We'll then just repeat that for trials 2 through 5.
We'll include post hoc tests too. Surprisingly, the dialog is only for between-subjects factors -which we don't have now. For within-subjects factors, use the dialog as shown below.
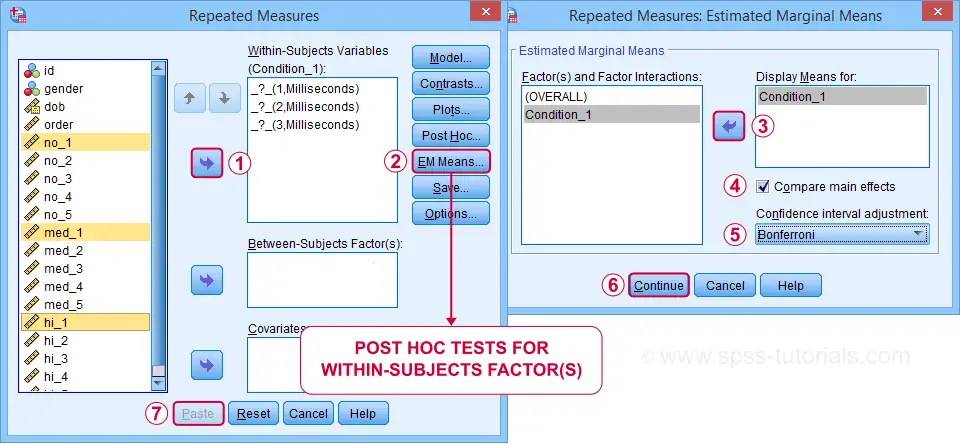
Completing these steps results in the syntax below.
GLM no_5 med_5 hi_5
/WSFACTOR=Condition_5 3 Polynomial
/MEASURE=Milliseconds
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(Condition_5) COMPARE ADJ(BONFERRONI)
/PRINT=ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=Condition_5.
Simple Effects Output I - Mauchly's Test

When comparing the 3 alcohol conditions for trial 1 only, Mauchly's test suggests that the sphericity assumption is violated. In this case, we report either
- the Greenhouse-Geisser corrected results or
- the Huyn-Feldt corrected results.
Precisely which depends on the Greenhouse-Geisser epsilon. Epsilon is the Greek letter e written as ε. It estimates to which extent sphericity holds. For this example, ε = 0.840 -a modest violation of sphericity. If ε > 0.75, we report the Huyn-Feldt corrected results as shown below.
Repeated Measures ANOVA - Sphericity Flowchart
Simple Effects Output II - Within-Subjects Effects

For trial 1, the 3 mean reaction times are significantly different because “Sig.” or p < 0.05. However, note that the effect size -partial eta squared- is modest: η2 = 0.207.
In any case, we conclude that the 3 means are not all equal. However, we don't know precisely which means are (not) different. As suggested by our flowchart, we can find out from the post hoc tests we ran.
Simple Effects Output III - Post Hoc Tests
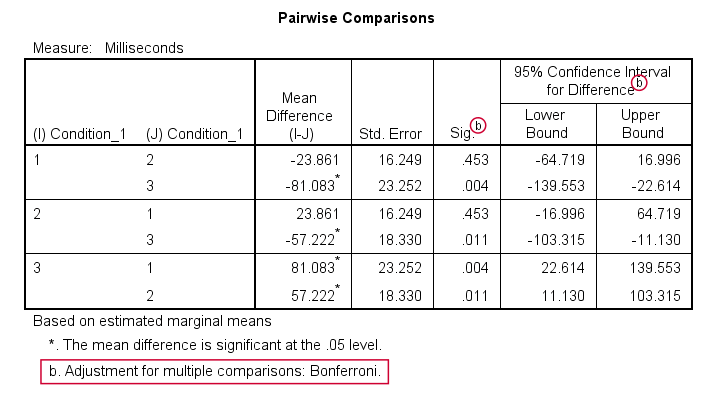
Precisely which means are (not) different? The Pairwise Comparisons table tells us that
only the mean difference between conditions 1 and 2
is not statistically significant.
So how do these tests work? What SPSS does here, is simply running a paired samples t-test between each pair of variables. For 3 conditions, this results in 3 such tests. Now, 3 tests have a bigger chance of coming up with a false result than 1 test. In order to correct for this, all p-values are multiplied by 3. This is the Bonferroni correction mentioned in the table comment. You can easily verify this by running
T-TEST PAIRS=no_1 med_1 hi_1.
This results in uncorrected p-values which are equal to the corrected p-values divided by 3.
So that'll do for trial 1. Analyzing trials 2-5 is left as an exercise to the reader.
Repeated Measures ANOVA - APA Style Reporting
First and foremost, present a table with descriptive statistics like the reporting table we created earlier.
Second, report the outcome of Mauchly's test for each effect you discuss:
“for trial 1, Mauchly's test indicated a violation
of the sphericity assumption, χ2(2) = 7.17, p = 0.028.”
If sphericity is violated, report the Greenhouse-Geisser ε and which corrected results you'll report:
“Since sphericity is violated (ε = 0.840),
Huyn-Feldt corrected results are reported.”
Finally, report the (corrected) F-test results for the within-subjects effects:
“Mean reaction times were affected by alcohol,
F(1.76,61.46) = 9.13, p = 0.001, η2 = 0.21.”
Note that η2 refers to (partial) eta squared, an effect size measure for ANOVA.
Thanks for reading.
SPSS Repeated Measures ANOVA Tutorial
- What is Repeated Measures ANOVA?
- Repeated Measures ANOVA Assumptions
- Quick Data Check
- Running Repeated Measures ANOVA in SPSS
- Interpreting the Output
- Reporting Repeated Measures ANOVA
1. What is Repeated Measures ANOVA?
SPSS repeated measures ANOVA tests if the means of 3 or more metric variables are all equal in some population. If this is true and we inspect a sample from our population, the sample means may differ a little bit. Large sample differences, however, are unlikely; these suggest that the population means weren't equal after all.
The simplest repeated measures ANOVA involves 3 outcome variables, all measured on 1 group of cases (often people). Whatever distinguishes these variables (sometimes just the time of measurement) is the within-subjects factor.
Repeated Measures ANOVA Example
A marketeer wants to launch a new commercial and has four concept versions. She shows the four concepts to 40 participants and asks them to rate each one of them on a 10-point scale, resulting in commercial_ratings.sav.Although such ratings are strictly ordinal variables, we'll treat them as metric variables under the assumption of equal intervals. Part of these data are shown below.

The research question is: which commercial has the highest mean rating? We'll first just inspect the mean ratings in our sample. We'll then try and generalize this sample outcome to our population by testing the null hypothesis that the 4 population mean scores are all equal. We'll reject this if our sample means are very different. Reversely, our sample means being slightly different is a normal sample outcome if population means are all similar.
2. Assumptions Repeated Measures ANOVA
Running a statistical test doesn't always make sense; results reflect reality only insofar as relevant assumptions are met. For a (single factor) repeated measures ANOVA these are
- Independent observations (or, more precisely, independent and identically distributed variables). This is often -not always- satisfied by each case in SPSS representing a different person or other statistical unit.
- The test variables follow a multivariate normal distribution in the population. However, this assumption is not needed if the sample size >= 25.
- Sphericity. This means that the population variances of all possible difference scores (com_1 - com_2, com_1 - com_3 and so on) are equal. Sphericity is tested with Mauchly’s test which is always included in SPSS’ repeated measures ANOVA output so we'll get to that later.
3. Quick Data Check
Before jumping blindly into statistical tests, let's first get a rough idea of what the data look like. Do the frequency distributions look plausible? Are there any system missing values or user missing values that we need to define? For quickly answering such questions, we'll open the data and run histograms with the syntax below.
frequencies com_1 to com_4
/format notable
/histogram.
Result
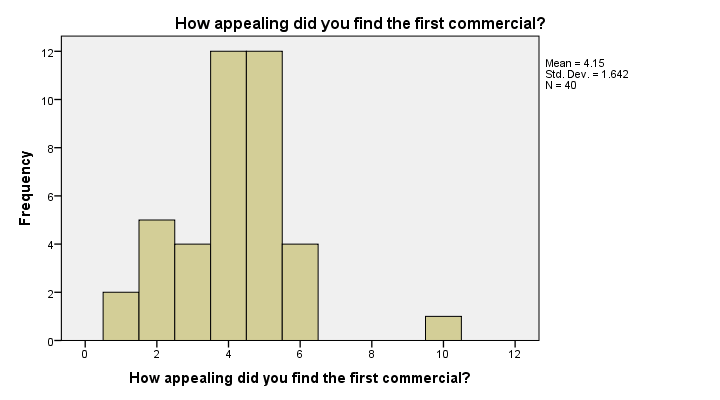
First off, our histograms look plausible and don't show any weird patterns or extreme values. There's no need to exclude any cases or define user missing values.
Second, since n = 40 for all variables, we don't have any system missing values. In this case, we can proceed with confidence.
4. Run SPSS Repeated Measures ANOVA
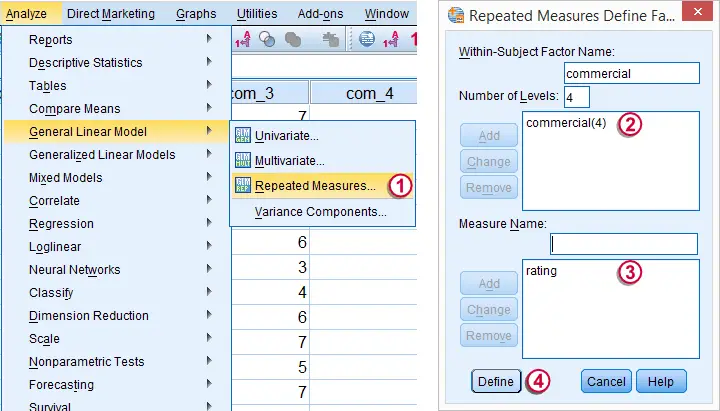
 We may freely choose a name for our within-subjects factor. We went with “commercial” because it's the commercial that differs between the four ratings made by each respondent.
We may freely choose a name for our within-subjects factor. We went with “commercial” because it's the commercial that differs between the four ratings made by each respondent.
 We may also choose a name for our measure: whatever each of the four variables is supposed to reflect. In this case we simply chose “rating”.
We may also choose a name for our measure: whatever each of the four variables is supposed to reflect. In this case we simply chose “rating”.
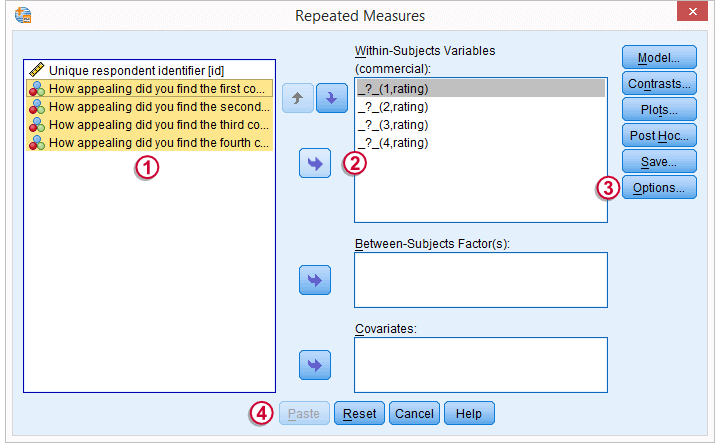
 We now select all four variables and move them to the box with
We now select all four variables and move them to the box with  the arrow to the right.
the arrow to the right.
 Under we'll select .
Under we'll select .
 Clicking results in the syntax below.
Clicking results in the syntax below.
GLM com_1 com_2 com_3 com_4
/WSFACTOR=commercial 4 Polynomial
/MEASURE=rating
/METHOD=SSTYPE(3)
/PRINT=DESCRIPTIVE
/CRITERIA=ALPHA(.05)
/WSDESIGN=commercial.
5. Repeated Measures ANOVA Output - Descriptives
First off, we take a look at the Descriptive Statistics table shown below. Commercial 4 was rated best (m = 6.25). Commercial 1 was rated worst (m = 4.15). Given our 10-point scale, these are large differences.

Repeated Measures ANOVA Output - Mauchly’s Test
We now turn to Mauchly's test for the sphericity assumption. As a rule of thumb, sphericity is assumed if Sig. > 0.05. For our data, Sig. = 0.54 so sphericity is no issue here.

The amount of sphericity is estimated by epsilon (the Greek letter ‘e’ and written as ε). There are different ways for estimating it, including the Greenhouse-Geisser, Huynh-Feldt and lower bound methods. If sphericity is violated, these are used to correct the within-subjects tests as we'll see below.If sphericity is very badly violated, we may report the Multivariate Tests table or abandon repeated measures ANOVA altogether in favor of a Friedman test.
Repeated Measures ANOVA Output - Within-Subjects Effects
Since our data seem spherical, we'll ignore the Greenhouse-Geisser, Huynh-Feldt and lower bound results in the table below. We'll simply interpret the uncorrected results denoted as “Sphericity Assumed”.

The Tests of Within-Subjects Effects is our core output. Because we've just one factor (which commercial was rated), it's pretty simple.
 Our p-value, Sig. = .000. So if the means are perfectly equal in the population, there's a 0% chance of finding the differences between the means that we observe in the sample. We therefore reject the null hypothesis of equal means.
Our p-value, Sig. = .000. So if the means are perfectly equal in the population, there's a 0% chance of finding the differences between the means that we observe in the sample. We therefore reject the null hypothesis of equal means.
 The F-value is not really interesting but we'll report it anyway. The same goes for
The F-value is not really interesting but we'll report it anyway. The same goes for  the effect degrees of freedom (df1) and
the effect degrees of freedom (df1) and  the error degrees of freedom (df2).
the error degrees of freedom (df2).
6. Reporting the Measures ANOVA Result
When reporting a basic repeated-measures ANOVA, we usually report
- the descriptive statistics table
- the outcome of Mauchly's test and
- the outcome of the within-subjects tests.
When reporting corrected results (Greenhouse-Geisser, Huynh-Feldt or lower bound), indicate which of these corrections you used. We'll cover this in SPSS Repeated Measures ANOVA - Example 2.
Finally, the main F-test is reported as
“The four commercials were not rated equally,
F(3,117) = 15.4, p = .000.”
Thank you for reading!
Repeated Measures ANOVA – Simple Introduction
Null Hypothesis
The null hypothesis for a repeated measures ANOVA is that 3(+) metric variables have identical means in some population.

The variables are measured on the same subjects so we're looking for within-subjects effects (differences among means). This basic idea is also referred to as dependent, paired or related samples in -for example- nonparametric tests.
But anyway: if all population means are really equal, we'll probably find slightly different means in a sample from this population. However, very different sample means are unlikely in this case. These would suggest that the population means weren't equal after all.
Repeated measures ANOVA basically tells us how likely our sample mean differences are if all means are equal in the entire population.
Repeated Measures ANOVA - Assumptions
- Independent observations or, precisely, Independent and identically distributed variables;
- Normality: the test variables follow a multivariate normal distribution in the population;
- Sphericity: the variances of all difference scores among the test variables must be equal in the population. Sphericity is sometimes tested with Mauchly’s test. If sphericity is rejected, results may be corrected with the Huynh-Feldt or Greenhouse-Geisser correction.
Repeated Measures ANOVA - Basic Idea
We'll show some example calculations in a minute. But first: how does repeated measures ANOVA basically work? First off, our outcome variables vary between and within our subjects. That is, differences between and within subjects add up to a total amount of variation among scores. This amount of variation is denoted as SStotal where SS is short for “sums of squares”.
We'll then split our total variance into components and inspect which component accounts for how much variance as outlined below. Note that “df” means “degrees of freedom”, which we'll get to later.
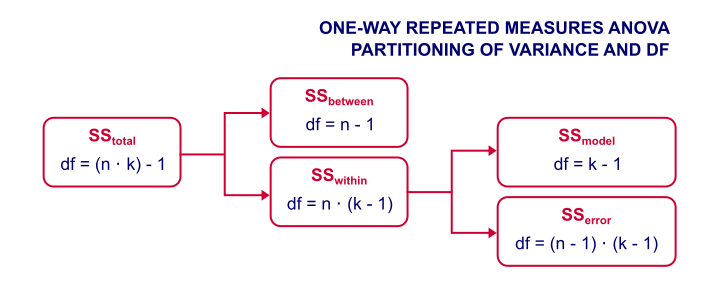
Now, we're not interested in how the scores differ between subjects. We therefore remove this variance from the total variance and ignore it. We're then left with just SSwithin (variation within subjects).
The variation within subjects may be partly due to our variables having different means. These different means make up our model. SSmodel is the amount of variation it accounts for.
Next, our model doesn't usually account for all of the variation between scores within our subjects. SSerror is the amount of variance that our model does not account for.
Finally, we compare two sources of variance: if SSmodel is large and SSerror is small, then variation within subjects is mostly due to our model (consisting of different variable means). This results in a large F-value, which is unlikely if the population means are really equal. In this case, we'll reject the null hypothesis and conclude that the population means aren't equal after all.
Repeated Measures ANOVA - Basic Formulas
We'll use the following notation in our formulas:
- \(n\) denotes the number of subjects;
- \(k\) denotes the number of variables;
- \(Xij\) denotes the score of subject \(i\) on variable \(j\);
- \(Xi.\) denotes the mean for subject \(i\);
- \(X.j\) denotes the mean of variable \(j\);
- \(X..\) denotes the grand mean.
Now, the formulas for the sums of squares, degrees of freedom and mean squares are
$$SS_{within} = \sum_{i=1}^n\sum_{j=1}^k(Xij - Xi.)^2$$
$$SS_{model} = n \sum_{j=1}^k(X.j - X..)^2$$
$$SS_{error} = SS_{within} - SS_{model}$$
$$df_{model} = k - 1$$
$$df_{error} = (k - 1)\cdot(n - 1)$$
$$MS_{model} = \frac{SS_{model}}{df_{model}}$$
$$MS_{error} = \frac{SS_{error}}{df_{error}}$$
$$F = \frac{MS_{model}}{MS_{error}}$$
Repeated Measures ANOVA - Example
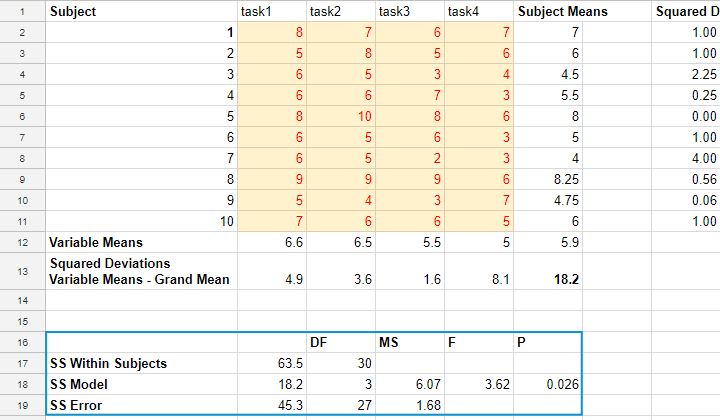
We had 10 people perform 4 memory tasks. The data thus collected are listed in the table below. We'd like to know if the population mean scores for all four tasks are equal.
| Subject | task1 | task2 | task3 | task4 | Subject Mean |
|---|---|---|---|---|---|
| 1 | 8 | 7 | 6 | 7 | 7 |
| 2 | 5 | 8 | 5 | 6 | 6 |
| 3 | 6 | 5 | 3 | 4 | 4.5 |
| 4 | 6 | 6 | 7 | 3 | 5.5 |
| 5 | 8 | 10 | 8 | 6 | 8 |
| 6 | 6 | 5 | 6 | 3 | 5 |
| 7 | 6 | 5 | 2 | 3 | 4 |
| 8 | 9 | 9 | 9 | 6 | 8.25 |
| 9 | 5 | 4 | 3 | 7 | 4.75 |
| 10 | 7 | 6 | 6 | 5 | 6 |
| Variable Mean | 6.6 | 6.5 | 5.5 | 5 | 5.9 (grand mean) |
If we apply our formulas to our example data, we'll get
$$SS_{within} = (8 - 7)^2 + (7 - 7)^2 + ... + (5 - 6)^2 = 63.5$$
$$SS_{model} = 10 \cdot((6.6 - 5.9)^2 + (6.5 - 5.9)^2 + (5.5 - 5.9)^2 + (5 - 5.9)^2) = 18.2$$
$$SS_{error} = 63.5 - 18.2 = 45.3$$
$$MS_{model} = \frac{18.2}{3} = 6.07$$
$$MS_{error} = \frac{45.3}{27} = 1.68$$
$$F = \frac{6.07}{1.68} = 3.62$$
$$P(F(3,27) > 3.62) \approx 0.026$$
The null hypothesis is usually rejected when p < 0.05. Conclusion: the population means probably weren't equal after all.
Repeated Measures ANOVA - Software
We computed the entire example in the Googlesheet shown below. It's accessible to all readers so feel free to take a look at the formulas we use.
Although you can run the test in a Googlesheet, you probably want to use decent software for running a repeated measures ANOVA. It's not included in SPSS by default unless you have the advanced statistics option installed. An outstanding example of repeated measures ANOVA in SPSS is SPSS Repeated Measures ANOVA.
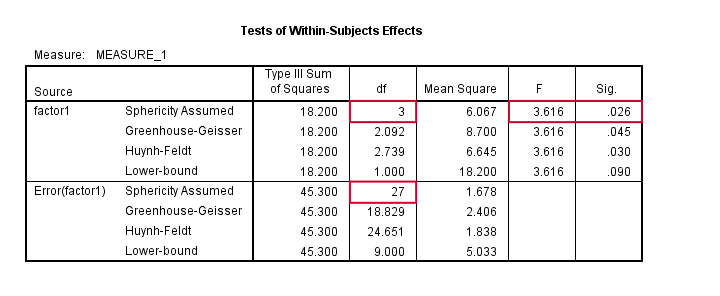
The figure below shows the SPSS output for the example we ran in this tutorial.
Factorial Repeated Measures ANOVA
Thus far, our discussion was limited to one-way repeated measures ANOVA with a single within-subjects factor. We can easily extend this to a factorial repeated measures ANOVA with one within-subjects and one between-subjects factor. The basic idea is shown below. For a nice example in SPSS, see SPSS Repeated Measures ANOVA - Example 2.
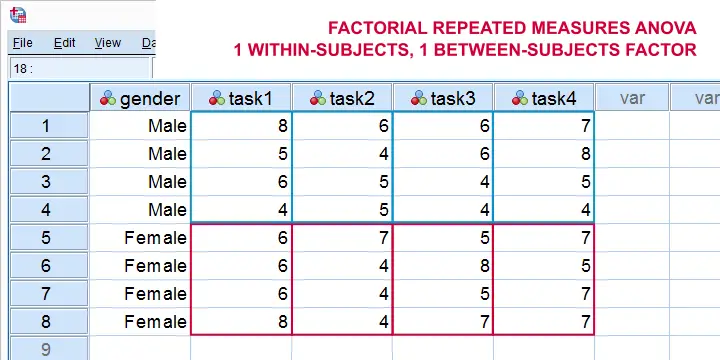
Alternatively, we can extend our model to a factorial repeated measures ANOVA with 2 within-subjects factors. The figure below illustrates the basic idea.
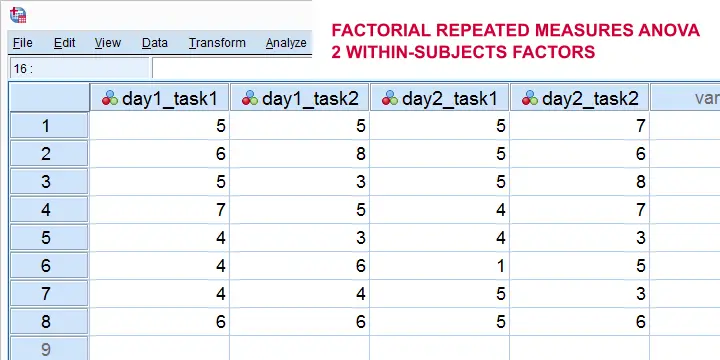
Finally, we could further extend our model into a 3(+) way repeated measures ANOVA. (We speak of “repeated measures ANOVA” if our model contains at least 1 within-subjects factor.)
Right, so that's about it I guess. I hope this tutorial has clarified some basics of repeated measures ANOVA.
Thanks for reading!
SPSS Repeated Measures ANOVA II
For reading up on some basics, see ANOVA - What Is It?
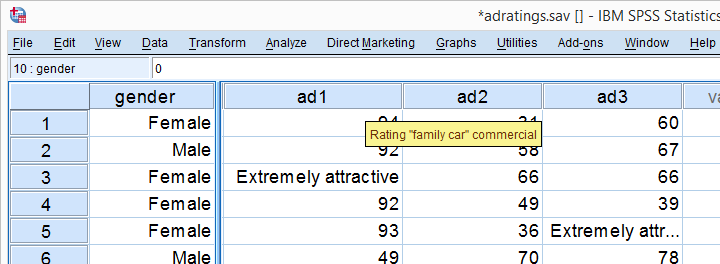
A car brand had 18 respondents rate 3 different car ads on attractiveness. The resulting data -part of which are shown above- are in adratings.sav. Some background variables were measured as well, including the respondent’s gender. The question we'll try to answer is: are the 3 ads rated equally attractive and does gender play any role here? Since we'll compare the means of 3(+) variables measured on the same respondents, we'll run a repeated measures ANOVA on our data. We'll first overview a simple but solid approach for the entire process. We'll then explain the what and why of each of these steps as we'll carry out the analysis step-by-step.
Factorial ANOVA - Basic Workflow
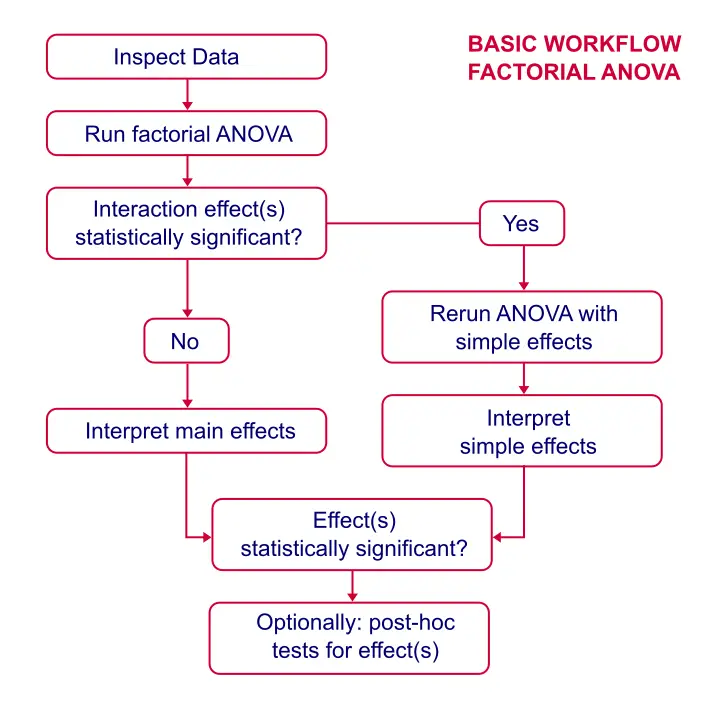
Data Inspection
First, we're not going to analyze any variables if we don't have a clue what's in them. The very least we'll do is inspect some histograms for outliers, missing values or weird patterns. For gender, a bar chart would be more appropriate but the histogram will do.
SPSS Basic Histogram Syntax
frequencies gender ad1 to ad3/format notable/histogram.
You can now verify for yourself that all distributions look plausible and there's no missing values or other issues with these variables.
Assumptions for Repeated Measures ANOVA
- Independent and identically distributed variables (“independent observations”).
- Normality: the test variables follow a multivariate normal distribution in the population.
- Sphericity: the variances of all difference scores among the test variables must be equal in the population.1, 2, 3
First, since each case (row of data cells) in SPSS holds a different person, the observations are probably independent.
Regarding the normality assumption, our previous histograms showed some skewness but nothing too alarming.
Last, Mauchly’s test for the sphericity assumption will be included in the output so we'll see if that holds in a minute.
Running Repeated Measures ANOVA in SPSS
We'll first run a very basic analysis by following the screenshots below. The initial results will then suggest how to nicely fine tune our analysis in a second run.
may be absent from your menu if you don't have the SPSS option “Advanced statistics” installed. You can verify this by running show license.
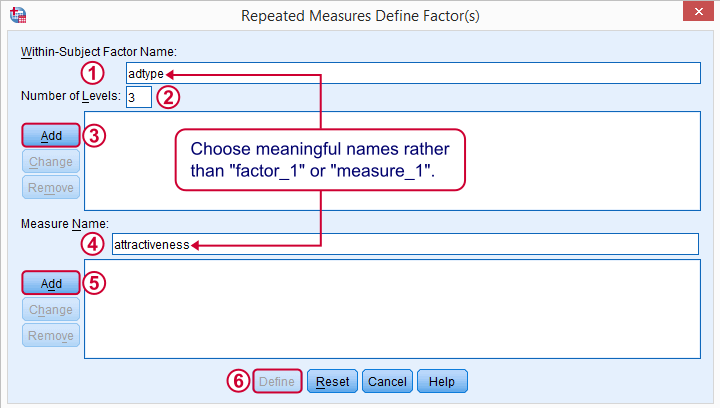
The within-subjects factor is whatever distinguishes the three variables we'll compare. We recommend you choose a meaningful name for it.
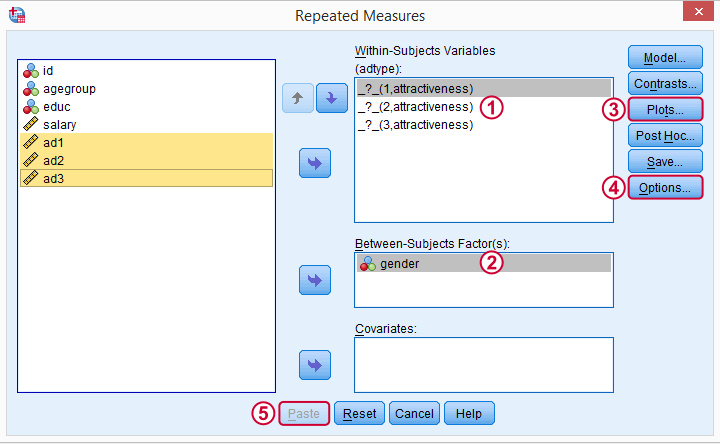
Select and move the three adratings variables in one go to the within-subjects variables box. Move gender into the between-subjects factor box.
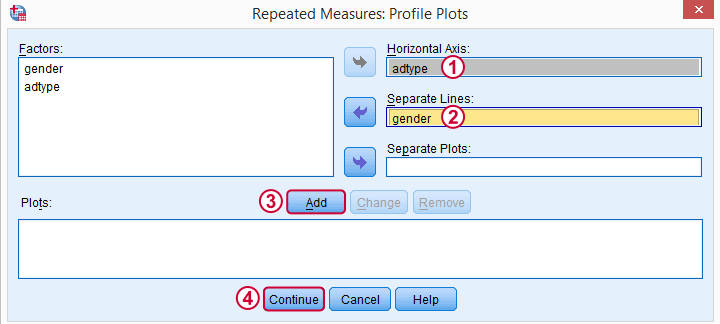
These profile plots will nicely visualize our 6 means (3 ads for 2 genders) in a multiple line chart.
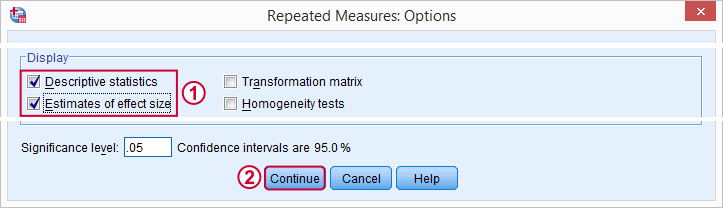
For now, we'll only tick and in the subdialog. Clicking in the main dialog results in the syntax below.
SPSS Basic Repeated Measures ANOVA Syntax
GLM ad1 ad2 ad3 BY gender
/WSFACTOR=adtype 3 Polynomial
/MEASURE=attractiveness
/METHOD=SSTYPE(3)
/PLOT=PROFILE(adtype*gender)
/PRINT=DESCRIPTIVE ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=adtype
/DESIGN=gender.
Output - Select and Reorder
Since we're not going to inspect all of our output, we'll first delete some items as shown below.
Next, we'll move our profile plots up by dragging and dropping it right underneath the descriptive statistics table.
Output - Means Plot and Descriptives
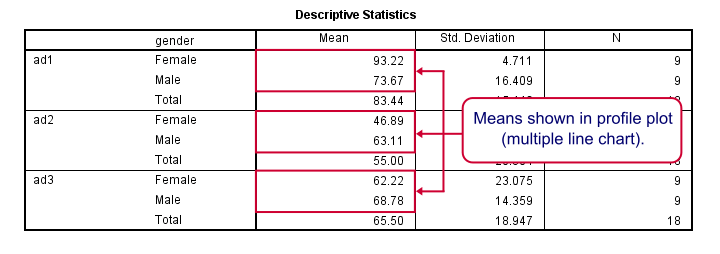
At the very core of our output, we just have 6 means: 3 ads for men and women separately. Both men and women rate adtype 1 (“family car”, as seen in the variable labels) most attractive. Adtype 2 (“youngster car”) is rated worst and adtype 3 is in between.Technical note: these means may differ from DESCRIPTIVES output because the repeated measures procedure excludes all cases with one or more missing values from the entire procedure.
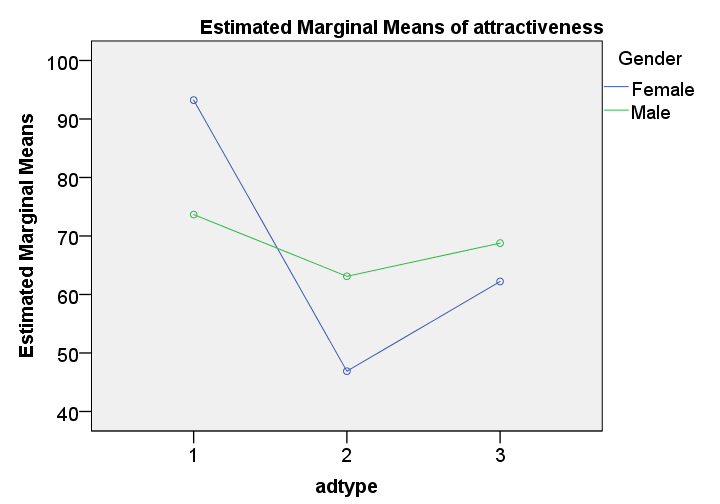
These means are nicely visualized in our profile plot.The “estimated marginal means” are equal to the observed means for the saturated model (all possible effects included). By default, SPSS always tests the saturated model for any factorial ANOVA. Now, what's really important is that the lines are far from parallel. This suggests an interaction effect: the effect of adtype is different for men and women.
Roughly, the line is almost horizontal for men: the three ads are rated quite similarly. For women, however, there's a huge difference between ad1 and ad2.
Keep in mind, however, that this is just a sample. Are the differences we see large enough for concluding anything about the entire population from which our sample was drawn? The answer is a clear “yes!” as we'll see in a minute.
Output - Mauchly’s Test
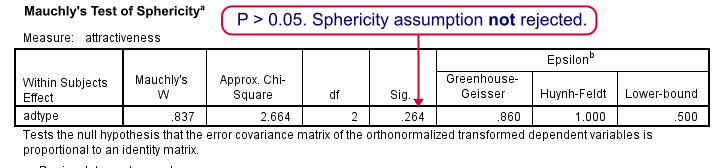
As we mentioned under assumptions, repeated measures ANOVA requires sphericity and Mauchly’s test evaluates if this holds. The p-value (denoted by “Sig.”) is 0.264. We usually state that sphericity is met if p > 0.05, so the sphericity assumption is met by our data. We don't need any correction such as Greenhouse-Geisser of Huynh-Feldt. The flowchart below suggests which results to report if sphericity does (not) hold.

Output - Within-Subjects Effects
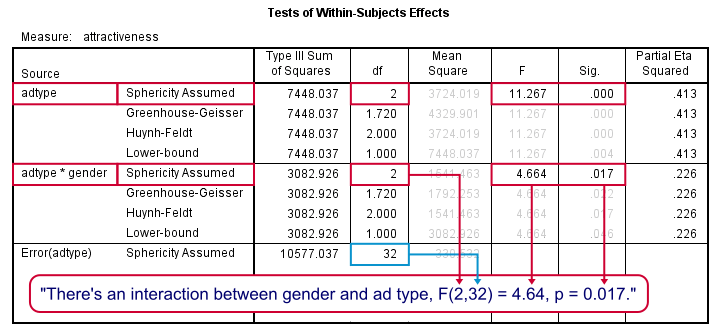
First, the interaction effect between gender and adtype has a p-value (“Sig.”) of 0.017. If p < 0.05, we usually label an effect “statistically significant” so we have an interaction effect indeed as suggested by our profile plot.
This plot shows that the effects for adtype are clearly different for men and women. So we should test the effects of adtype for male and female respondents separately. These are called simple effects as shown in our flowchart.
There is a strong main effect for adtype: F(2,32) = 11.27, p = 0.000 too. But as suggested by our flowchart, we'll ignore it. The main effect lumps together men and women, which is justifiable only if these show similar effects for adtype. That is: if the lines in our profile plot would run roughly parallel but that's not the case here.
In other words, there's no such thing as the effect of adtype as a main effect suggests. The separate effects of adtype for men and women would be obscured by taking them together so we'll analyze them separately (simple effects) instead.
Repeated Measures ANOVA - Simple Effects
There's no such thing as “simple effects” in SPSS’ menu. However, we can easily analyze male and female respondents separately with SPLIT FILE by running the syntax below.
sort cases by gender.
split file by gender.
Repeated Measures ANOVA - Second Run
The SPLIT FILE we just allows us to analyze simple effects: repeated measures ANOVA output for men and women separately. We can either rerun the analysis from the main menu or use the dialog recall button ![]() as a handy shortcut.
as a handy shortcut.
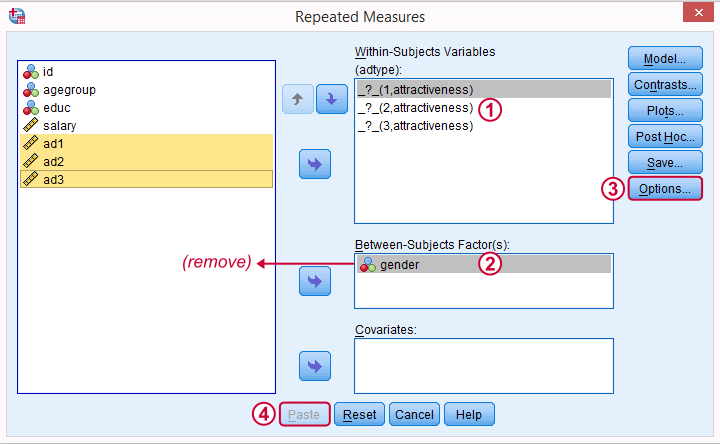
We remove gender from the between-subjects factor box. Because the analysis is run for men and women separately, gender will be a constant in both groups.
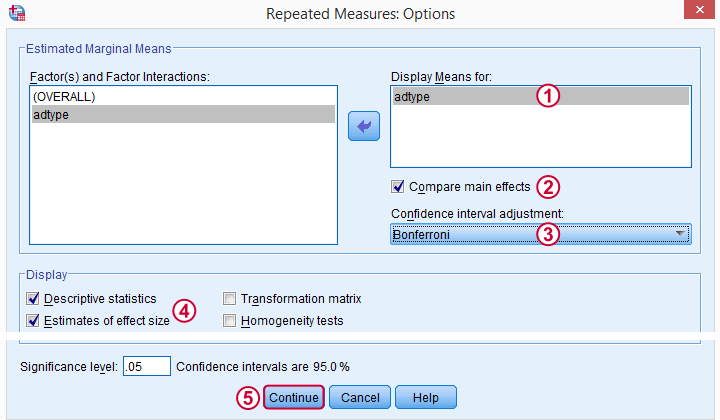
As suggested by our flowchart, we'll now add some post hoc tests. Post hoc tests for within-subjects factors (adtype in our case) are well hidden behind the rather than the button. The latter only allows post hoc tests for between-subjects effects, which we no longer have.
Repeated Measures ANOVA - Simple Effects Syntax
GLM ad1 ad2 ad3
/WSFACTOR=adtype 3 Polynomial
/MEASURE=attractiveness
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(adtype) COMPARE ADJ(BONFERRONI)
/PRINT=DESCRIPTIVE ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=adtype.
Simple Effects - Output
We interpret most output as previously discussed. Note that adtype has an effect for female respondents: F(2,16) = 11.68, p = 0.001. The precise meaning of this is that if all three population mean ratings would be equal, we would have a 0.001 (or 0.1%) chance of finding the mean differences we observe in our sample.
For males, this effect is not statistically significant: F(2,16) = 1.08, p = .362: if the 3 population means are really equal, we have a 36% chance of finding our sample differences; what we see in our sample does not negate our null hypothesis.
Output - Post Hoc Tests
Right, we just concluded that adtype is related to rating for female but not male respondents. We'll therefore interpret the post hoc results for female respondents only and ignore those for male respondents.
But why run post hoc tests in the first place? Well, we concluded that the null hypothesis of all population mean rating equal is not tenable. However, with 3 or more means, we don't know exactly which means are different. A post hoc (Latin for “after that”) test -as suggested by our flowchart- will tell us just that.
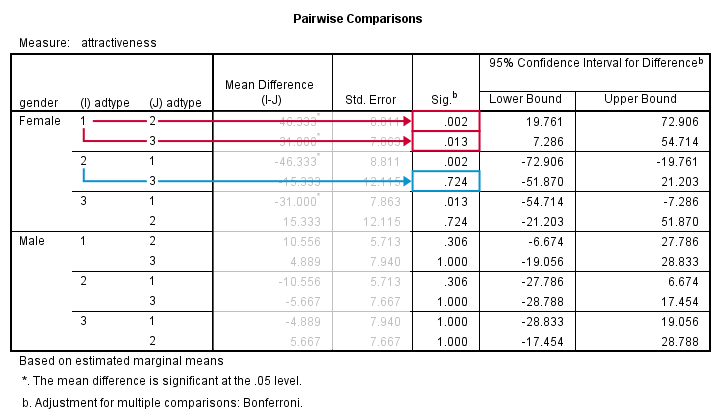
With 3 means, we've 3 comparisons and each of them is listed twice in this table; 1 versus 3 is obviously the same as 3 versus 1. We quickly see that ad1 differs from ad2 and ad3. The difference between ad2 and ad3, however, is not statistically significant. Unfortunately, SPSS doesn't provide the t-values and degrees of freedom needed for reporting these results.
An alternative way to obtain these is running paired samples t-tests on all pairs of variables. The Bonferroni correction means that we'll multiply all p-values by the number of tests we're running (3 in this case). Doing so is left as an exercise to the reader.
Thanks for reading!
References
- Field, A. (2013). Discovering Statistics with IBM SPSS Newbury Park, CA: Sage.
- Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
- Wijnen, K., Janssens, W., De Pelsmacker, P. & Van Kenhove, P. (2002). Marktonderzoek met SPSS: statistische verwerking en interpretatie [Market Research with SPSS: statistical processing and interpretation]. Leuven: Garant Uitgevers.
 SPSS TUTORIALS
SPSS TUTORIALS