Effect Size in Statistics - The Ultimate Guide

Effect Size – A Quick Guide

Effect size is an interpretable number that quantifies
the difference between data and some hypothesis.

Overview Effect Size Measures
Chi-Square Tests
T-Tests
Pearson Correlations
ANOVA
Linear Regression

Statistical significance is roughly the probability of finding your data if some hypothesis is true. If this probability is low, then this hypothesis probably wasn't true after all. This may be a nice first step, but what we really need to know is how much do the data differ from the hypothesis? An effect size measure summarizes the answer in a single, interpretable number. This is important because

effect sizes allow us to compare effects -both within and across studies;
we need an effect size measure to estimate (1 - β) or power. This is the probability of rejecting some null hypothesis given some alternative hypothesis;
even before collecting any data, effect sizes tell us which sample sizes we need to obtain a given level of power -often 0.80.

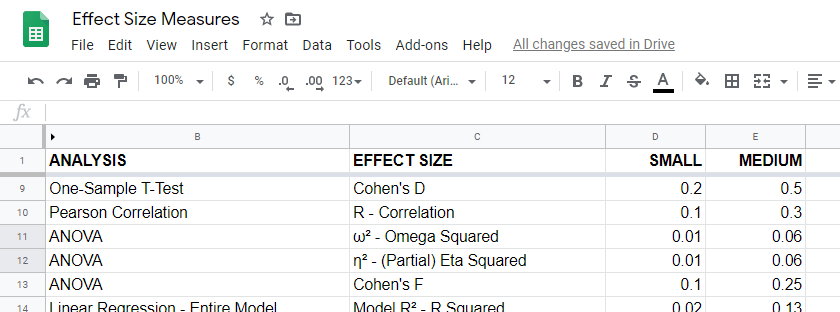
Overview Effect Size Measures

For an overview of effect size measures, please consult this Googlesheet shown below. This Googlesheet is read-only but can be downloaded and shared as Excel for sorting, filtering and editing.

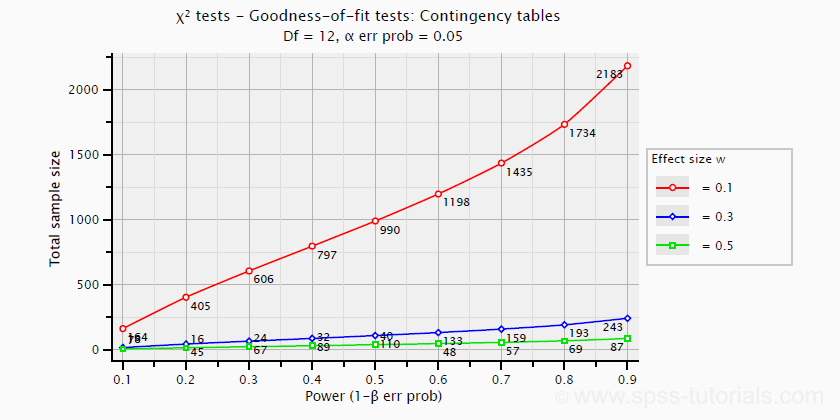
Chi-Square Tests

Common effect size measures for chi-square tests are

Cohen’s W (both chi-square tests);
Cramér’s V (chi-square independence test) and
the contingency coefficient (chi-square independence test) .

Chi-Square Tests - Cohen’s W

Cohen’s W is the effect size measure of choice for

the chi-square independence test and
the chi-square goodness-of-fit test.

Basic rules of thumb for Cohen’s W⁸ are

small effect: w = 0.10;
medium effect: w = 0.30;
large effect: w = 0.50.

Cohen’s W is computed as

$$W = \sqrt{\sum_{i = 1}^m\frac{(P_{oi} - P_{ei})^2}{P_{ei}}}$$

where

$P_{oi}$ denotes observed proportions and
$P_{ei}$ denotes expected proportions under the null hypothesis for
$m$ cells.

For contingency tables, Cohen’s W can also be computed from the contingency coefficient $C$ as

$$W = \sqrt{\frac{C^2}{1 - C^2}}$$

A third option for contingency tables is to compute Cohen’s W from Cramér’s V as

$$W = V \sqrt{d_{min} - 1}$$

where

$V$ denotes Cramér's V and
$d_{min}$ denotes the smallest table dimension -either the number of rows or columns.

Cohen’s W is not available from any statistical packages we know. For contingency tables, we recommend computing it from the aforementioned contingency coefficient.

For chi-square goodness-of-fit tests for frequency distributions your best option is probably to compute it manually in some spreadsheet editor. An example calculation is presented in this Googlesheet.

Power and required sample sizes for chi-square tests can't be directly computed from Cohen’s W: they depend on the df -short for degrees of freedom- for the test. The example chart below applies to a 5 · 4 table, hence df = (5 - 1) · (4 -1) = 12.

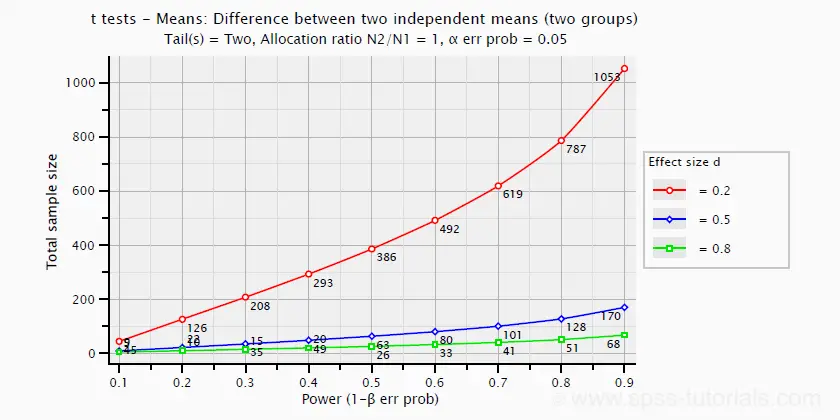
T-Tests

Common effect size measures for t-tests are

Cohen’s D (all t-tests) and
the point-biserial correlation (only independent samples t-test).

T-Tests - Cohen’s D

Cohen’s D is the effect size measure of choice for all 3 t-tests:

Basic rules of thumb are that⁸

|d| = 0.20 indicates a small effect;
|d| = 0.50 indicates a medium effect;
|d| = 0.80 indicates a large effect.

For an independent-samples t-test, Cohen’s D is computed as

$$D = \frac{M_1 - M_2}{S_p}$$

where

$M_1$ and $M_2$ denote the sample means for groups 1 and 2 and
$S_p$ denotes the pooled estimated population standard deviation.

A paired-samples t-test is technically a one-sample t-test on difference scores. For this test, Cohen’s D is computed as

$$D = \frac{M - \mu_0}{S}$$

where

$M$ denotes the sample mean,
$\mu_0$ denotes the hypothesized population mean (difference) and
$S$ denotes the estimated population standard deviation.

Cohen’s D is present in JASP as well as SPSS (version 27 onwards). For a thorough tutorial, please consult Cohen’s D - Effect Size for T-Tests.

The chart below shows how power and required total sample size are related to Cohen’s D. It applies to an independent-samples t-test where both sample sizes are equal.

Independent Samplest Test Sample Size Power Curve

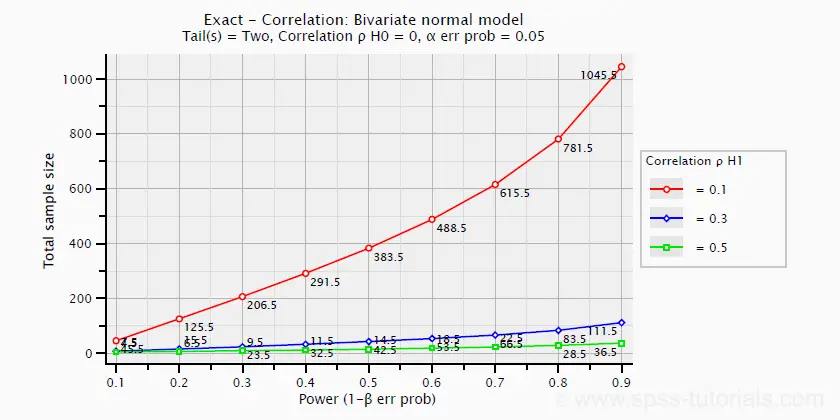
Pearson Correlations

For a Pearson correlation, the correlation itself (often denoted as r) is interpretable as an effect size measure. Basic rules of thumb are that⁸

r = 0.10 indicates a small effect;
r = 0.30 indicates a medium effect;
r = 0.50 indicates a large effect.

Pearson correlations are available from all statistical packages and spreadsheet editors including Excel and Google sheets.

The chart below -created in G*Power- shows how required sample size and power are related to effect size.

ANOVA

Common effect size measures for ANOVA are

$\color{#0a93cd}{\eta^2}$ or (partial) eta squared;
Cohen’s F;
$\color{#0a93cd}{\omega^2}$ or omega-squared.

ANOVA - (Partial) Eta Squared

Partial eta squared -denoted as η²- is the effect size of choice for

ANOVA (between-subjects, one-way or factorial);
repeated measures ANOVA (one-way or factorial);
mixed ANOVA.

Basic rules of thumb are that

η² = 0.01 indicates a small effect;
η² = 0.06 indicates a medium effect;
η² = 0.14 indicates a large effect.

Partial eta squared is calculated as

$$\eta^2_p = \frac{SS_{effect}}{SS_{effect} + SS_{error}}$$

where

$\eta^2_p$ denotes partial eta-squared and
$SS$ denotes effect and error sums of squares.

This formula also applies to one-way ANOVA, in which case partial eta squared is equal to eta squared.

Partial eta squared is available in all statistical packages we know, including JASP and SPSS. For the latter, see How to Get (Partial) Eta Squared from SPSS?

ANOVA - Cohen’s F

Cohen’s f is an effect size measure for

ANOVA (between-subjects, one-way or factorial);
repeated measures ANOVA (one-way or factorial);
mixed ANOVA.

Cohen’s f is computed as

$$f = \sqrt{\frac{\eta^2_p}{1 - \eta^2_p}}$$

where $\eta^2_p$ denotes (partial) eta-squared.

Basic rules of thumb for Cohen’s f are that⁸

f = 0.10 indicates a small effect;
f = 0.25 indicates a medium effect;
f = 0.40 indicates a large effect.

G*Power computes Cohen’s f from various other measures. We're not aware of any other software packages that compute Cohen’s f.

Power and required sample sizes for ANOVA can be computed from Cohen’s f and some other parameters. The example chart below shows how required sample size relates to power for small, medium and large effect sizes. It applies to a one-way ANOVA on 3 equally large groups.

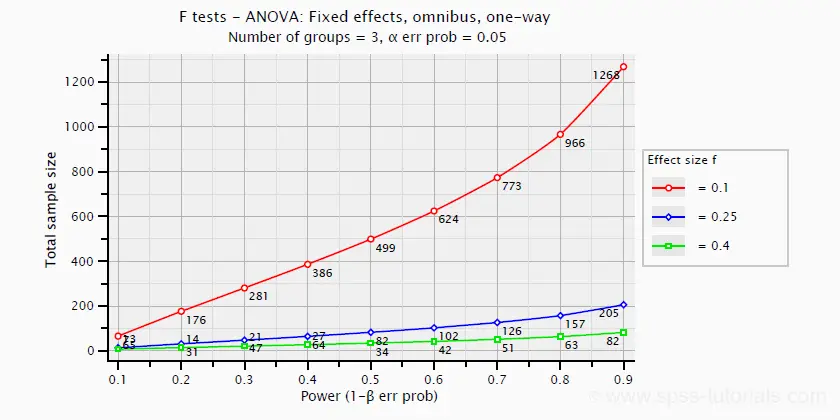
ANOVA - Omega Squared

A less common but better alternative for (partial) eta-squared is $\omega^2$ or Omega squared computed as

$$\omega^2 = \frac{SS_{effect} - df_{effect}\cdot MS_{error}}{SS_{total} + MS_{error}}$$

where

$SS$ denotes sums of squares;
$df$ denotes degrees of freedom;
$MS$ denotes mean squares.

Similarly to (partial) eta squared, $\omega^2$ estimates which proportion of variance in the outcome variable is accounted for by an effect in the entire population. The latter, however, is a less biased estimator.^1,2,6 Basic rules of thumb are⁵

Small effect: ω² = 0.01;
Medium effect: ω² = 0.06;
Large effect: ω² = 0.14.

$\omega^2$ is available in SPSS version 27 onwards but only if you run your ANOVA from Analyze Compare Means One-Way ANOVA The other ANOVA options in SPSS (via General Linear Model or Means) do not yet include $\omega^2$. However, it's also calculated pretty easily by copying a standard ANOVA table into Excel and entering the formula(s) manually.

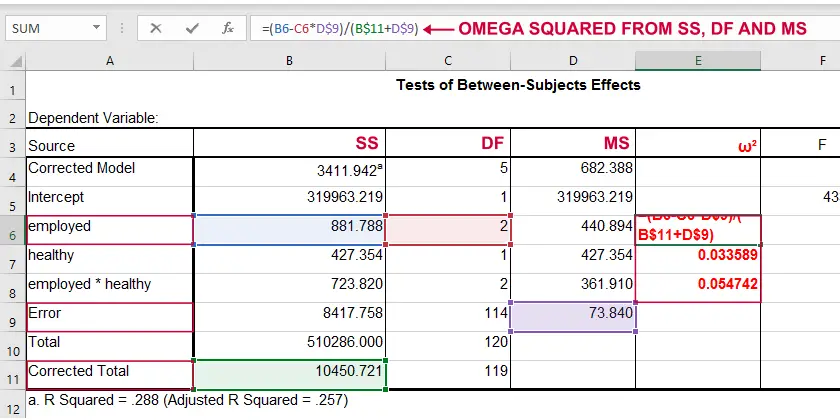Omega Squared Effect Size ANOVA In Excel

Note: you need “Corrected total” for computing omega-squared from SPSS output.

Linear Regression

Effect size measures for (simple and multiple) linear regression are

$\color{#0a93cd}{f^2}$ (entire model and individual predictor);
$R^2$ (entire model);
$r_{part}^2$ -squared semipartial (or “part”) correlation (individual predictor).

Linear Regression - F-Squared

The effect size measure of choice for (simple and multiple) linear regression is $f^2$. Basic rules of thumb are that⁸

$f^2$ = 0.02 indicates a small effect;
$f^2$ = 0.15 indicates a medium effect;
$f^2$ = 0.35 indicates a large effect.

$f^2$ is calculated as

$$f^2 = \frac{R_{inc}^2}{1 - R_{inc}^2}$$

where $R_{inc}^2$ denotes the increase in r-square for a set of predictors over another set of predictors. Both an entire multiple regression model and an individual predictor are special cases of this general formula.

For an entire model, $R_{inc}^2$ is the r-square increase for the predictors in the model over an empty set of predictors. Without any predictors, we estimate the grand mean of the dependent variable for each observation and we have $R^2 = 0$. In this case, $R_{inc}^2 = R^2_{model} - 0 = R^2_{model}$ -the “normal” r-square for a multiple regression model.

For an individual predictor, $R_{inc}^2$ is the r-square increase resulting from adding this predictor to the other predictor(s) already in the model. It is equal to $r^2_{part}$ -the squared semipartial (or “part”) correlation for some predictor. This makes it very easy to compute $f^2$ for individual predictors in Excel as shown below.

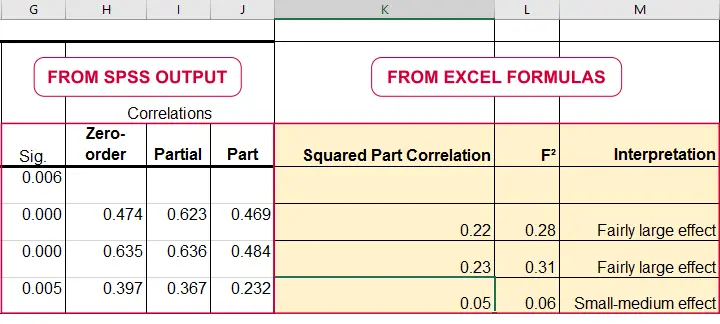
Multiple Regression Effect Size Individual Predictors

$f^2$ is useful for computing the power and/or required sample size for a regression model or individual predictor. However, these also depend on the number of predictors involved. The figure below shows how required sample size depends on required power and estimated (population) effect size for a multiple regression model with 3 predictors.

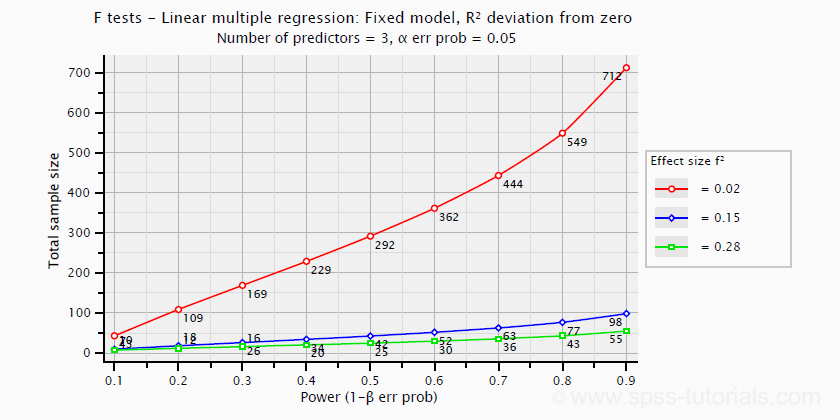
Linear Regression Power Sample Size Plot

Right, I think that should do for now. We deliberately limited this tutorial to the most important effect size measures in a (perhaps futile) attempt to not overwhelm our readers. If we missed something crucial, please throw us a comment below. Other than that,

thanks for reading!

References

Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [Statistics, part 3]. Amsterdam: Boom.
Warner, R.M. (2013). Applied Statistics (2nd. Edition). Thousand Oaks, CA: SAGE.
Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
Field, A. (2013). Discovering Statistics with IBM SPSS Statistics. Newbury Park, CA: Sage.
Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
Siegel, S. & Castellan, N.J. (1989). Nonparametric Statistics for the Behavioral Sciences (2nd ed.). Singapore: McGraw-Hill.
Cohen, J (1988). Statistical Power Analysis for the Social Sciences (2nd. Edition). Hillsdale, New Jersey, Lawrence Erlbaum Associates.
Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition). New York: Routledge.

Cohen’s D – Effect Size for T-Test

Cohen’s D is the difference between 2 means
expressed in standard deviations.

Cohen’s D - Formulas
Cohen’s D and Power
Cohen’s D & Point-Biserial Correlation
Cohen’s D - Interpretation
Cohen’s D for SPSS Users

Why Do We Need Cohen’s D?

Children from married and divorced parents completed some psychological tests: anxiety, depression and others. For comparing these 2 groups of children, their mean scores were compared using independent samples t-tests. The results are shown below.

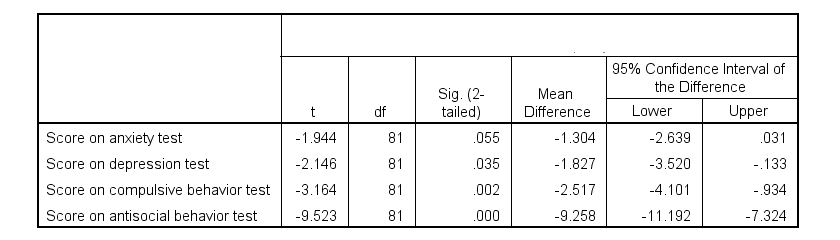
Some basic conclusions are that

all mean differences are negative. So the second group -children from divorced parents- have higher means on all tests.
Except for the anxiety test, all differences are statistically significant.
The mean differences range from -1.3 points to -9.3 points.

However, what we really want to know is are these small, medium or large differences? This is hard to answer for 2 reasons:

psychological test scores don't have any fixed unit of measurement such as meters, dollars or seconds.
Statistical significance does not imply practical significance (or reversely). This is because p-values strongly depend on sample sizes.

A solution to both problems is using the standard deviation as a unit of measurement like we do when computing z-scores. And a mean difference expressed in standard deviations -Cohen’s D- is an interpretable effect size measure for t-tests.

Cohen’s D - Formulas

Cohen’s D is computed as
$$D = \frac{M_1 - M_2}{S_p}$$
where

$M_1$ and $M_2$ denote the sample means for groups 1 and 2 and
$S_p$ denotes the pooled estimated population standard deviation.

But precisely what is the “pooled estimated population standard deviation”? Well, the independent-samples t-test assumes that the 2 groups we compare have the same population standard deviation. And we estimate it by “pooling” our 2 sample standard deviations with

$$S_p = \sqrt{\frac{(N_1 - 1) \cdot S_1^2 + (N_2 - 1) \cdot S_2^2}{N_1 + N_2 - 2}}$$

Fortunately, we rarely need this formula: SPSS, JASP and Excel readily compute a t-test with Cohen’s D for us.

Cohen’s D in JASP

Running the exact same t-tests in JASP and requesting “effect size” with confidence intervals results in the output shown below.

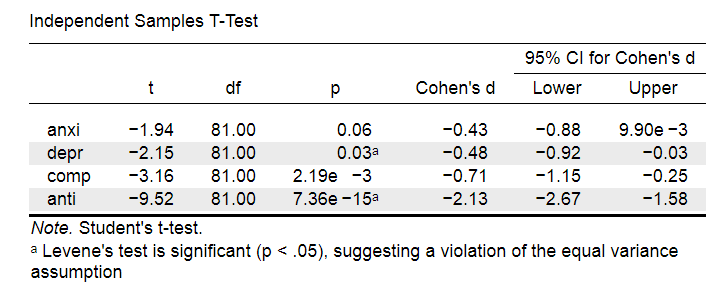
Note that Cohen’s D ranges from -0.43 through -2.13. Some minimal guidelines are that

d = 0.20 indicates a small effect,
d = 0.50 indicates a medium effect and
d = 0.80 indicates a large effect.

And there we have it. Roughly speaking, the effects for

the anxiety (d = -0.43) and depression tests (d = -0.48) are medium;
the compulsive behavior test (d = -0.71) is fairly large;
the antisocial behavior test (d = -2.13) is absolutely huge.

We'll go into the interpretation of Cohen’s D into much more detail later on. Let's first see how Cohen’s D relates to power and the point-biserial correlation, a different effect size measure for a t-test.

Cohen’s D and Power

Very interestingly, the power for a t-test can be computed directly from Cohen’s D. This requires specifying both sample sizes and α, usually 0.05. The illustration below -created with G*Power- shows how power increases with total sample size. It assumes that both samples are equally large.

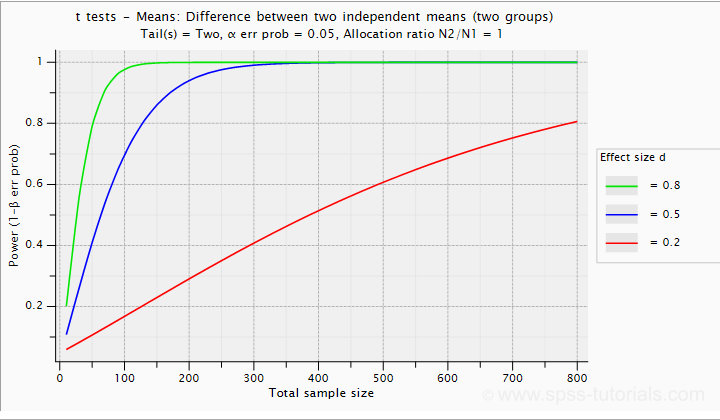
If we test at α = 0.05 and we want power (1 - β) = 0.8 then

use 2 samples of n = 26 (total N = 52) if we expect d = 0.8 (large effect);
use 2 samples of n = 64 (total N = 128) if we expect d = 0.5 (medium effect);
use 2 samples of n = 394 (total N = 788) if we expect d = 0.2 (small effect);

Cohen’s D and Overlapping Distributions

The assumptions for an independent-samples t-test are

independent observations;
normality: the outcome variable must be normally distributed in each subpopulation;
homogeneity: both subpopulations must have equal population standard deviations and -hence- variances.

If assumptions 2 and 3 are perfectly met, then Cohen’s D implies which percentage of the frequency distributions overlap. The example below shows how some male population overlaps with some 69% of some female population when Cohen’s D = 0.8, a large effect.

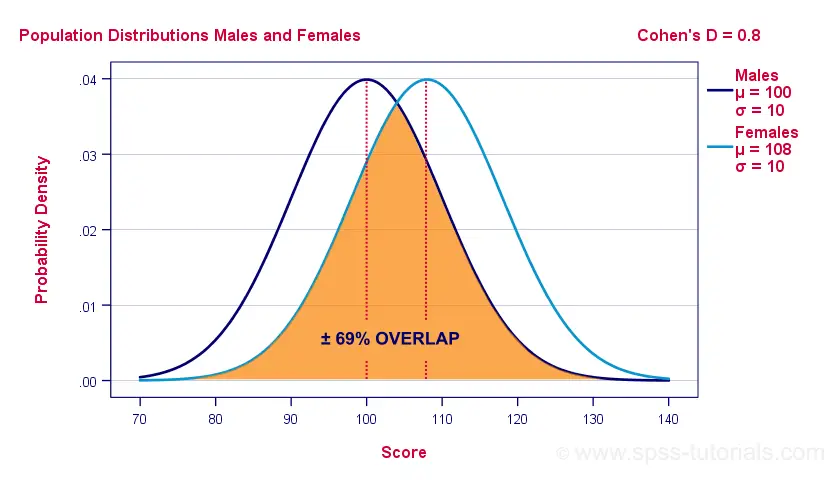
The percentage of overlap increases as Cohen’s D decreases. In this case, the distribution midpoints move towards each other. Some basic benchmarks are included in the interpretation table which we'll present in a minute.

Cohen’s D & Point-Biserial Correlation

An alternative effect size measure for the independent-samples t-test is $R_{pb}$, the point-biserial correlation. This is simply a Pearson correlation between a quantitative and a dichotomous variable. It can be computed from Cohen’s D with
$$R_{pb} = \frac{D}{\sqrt{D^2 + 4}}$$

For our 3 benchmark values,

Cohen’s d = 0.2 implies $R_{pb}$ ± 0.100;
Cohen’s d = 0.5 implies $R_{pb}$ ± 0.243;
Cohen’s d = 0.8 implies $R_{pb}$ ± 0.371.

Alternatively, compute $R_{pb}$ from the t-value and its degrees of freedom with
$$R_{pb} = \sqrt{\frac{t^2}{t^2 + df}}$$

Cohen’s D - Interpretation

The table below summarizes the rules of thumb regarding Cohen’s D that we discussed in the previous paragraphs.

Cohen’s D	Interpretation	Rpb	% overlap	Recommended N
d = 0.2	Small effect	± 0.100	± 92%	788
d = 0.5	Medium effect	± 0.243	± 80%	128
d = 0.8	Large effect	± 0.371	± 69%	52

Cohen’s D for SPSS Users

Cohen’s D is available in SPSS versions 27 and higher. It's obtained from Analyze Compare Means Independent Samples T Test as shown below.

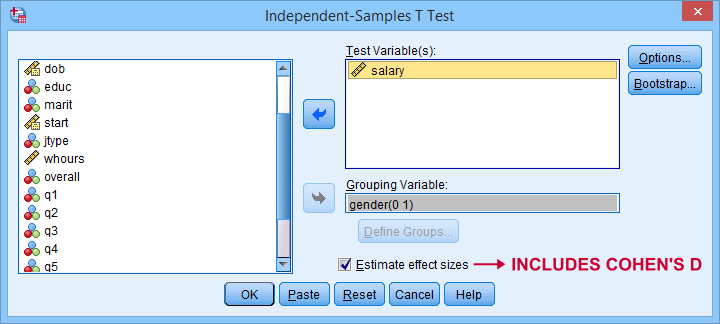
For more details on the output, please consult SPSS Independent Samples T-Test.

If you're using SPSS version 26 or lower, you can use Cohens-d.xlsx. This Excel sheet recomputes all output for one or many t-tests including Cohen’s D and its confidence interval from

both sample sizes,
both sample means and
both sample standard deviations.

The input for our example data in divorced.sav and a tiny section of the resulting output is shown below.

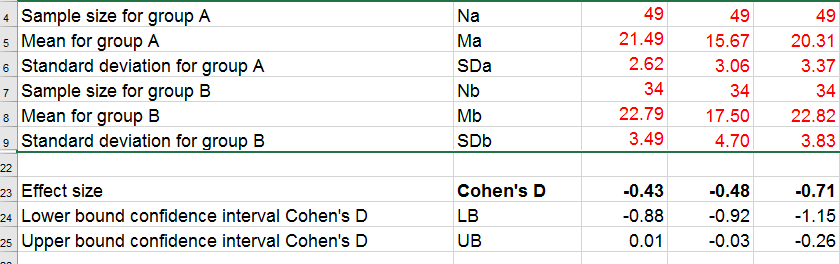
Note that the Excel tool doesn't require the raw data: a handful of descriptive statistics -possibly from a printed article- is sufficient.

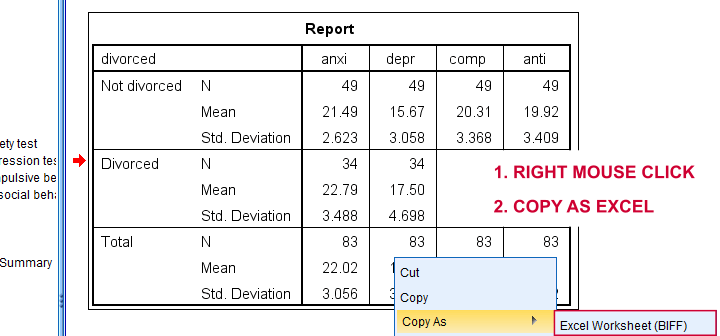
SPSS users can easily create the required input from a simple MEANS command if it includes at least 2 variables. An example is

*Create table with N, mean and SD for test scores by divorced for copying into Excel.

means anxi to anti by divorced
/cells count mean stddev.

Copy-pasting the SPSS output table as Excel preserves the (hidden) decimals of the results. These can be made visible in Excel and reduce rounding inaccuracies.

Final Notes

I think Cohen’s D is useful but I still prefer R², the squared (Pearson) correlation between the independent and dependent variable. Note that this is perfectly valid for dichotomous variables and also serves as the fundament for dummy variable regression.

The reason I prefer R² is that it's in line with other effect size measures: the independent-samples t-test is a special case of ANOVA. And if we run a t-test as an ANOVA, η² (eta squared) = R² or the proportion of variance accounted for by the independent variable. This raises the question: why should we use a different effect size measure
if we compare 2 instead of 3+ subpopulations? I think we shouldn't.

This line of reasoning also argues against reporting 1-tailed significance for t-tests: if we run a t-test as an ANOVA, the p-value is always the 2-tailed significance for the corresponding t-test. So why should you report a different measure for comparing 2 instead of 3+ means?

But anyway, that'll do for today. If you've any feedback -positive or negative- please drop us a comment below. And last but not least:

thanks for reading!