SPSS Mediation Analysis – The Complete Guide

• How to Examine Mediation Effects?
• SPSS Regression Dialogs
• SPSS Mediation Analysis Output
• APA Reporting Mediation Analysis
• Next Steps - The Sobel Test
• Next Steps - Index of Mediation

Example

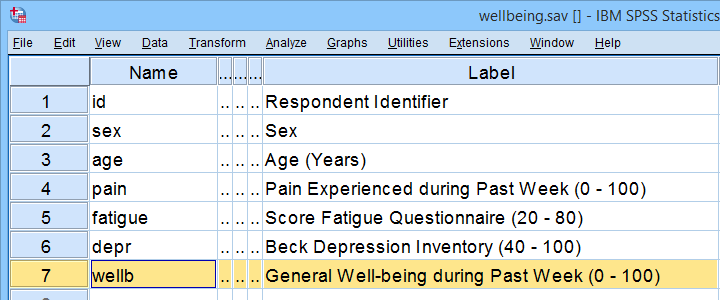
A scientist wants to know which factors affect general well-being among people suffering illnesses. In order to find out, she collects some data on a sample of N = 421 cancer patients. These data -partly shown below- are in wellbeing.sav.

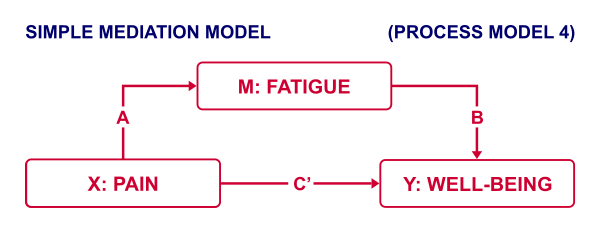
Now, our scientist believes that well-being is affected by pain as well as fatigue. On top of that, she believes that fatigue itself is also affected by pain. In short: pain partly affects well-being through fatigue. That is, fatigue mediates the effect from pain onto well-being as illustrated below.

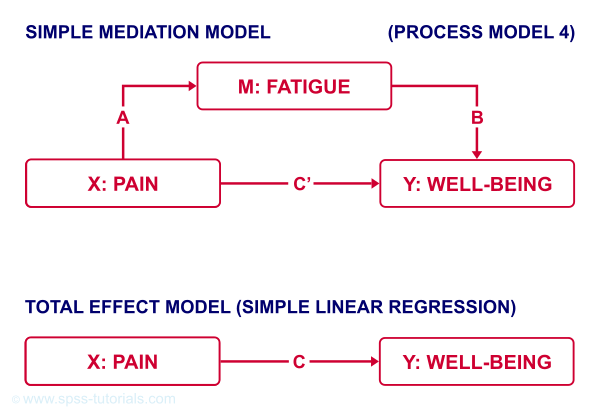
The lower half illustrates a model in which fatigue would (erroneously) be left out. This is known as the “total effect model” and is often compared with the mediation model above it.

How to Examine Mediation Effects?

Now, let's suppose for a second that all expectations from our scientist are exactly correct. If so, then what should we see in our data? The classical approach to mediation (see Kenny & Baron, 1986) says that

• \(a\) (from pain to fatigue) should be significant;
• \(b\) (from fatigue to well-being) should be significant;
• \(c\) (from pain to well-being) should be significant;
• \(c\,'\) (direct effect) should be closer to zero than \(c\) (total effect).

So how to find out if our data is in line with these statements? Well, all paths are technically just b-coefficients. We'll therefore run 3 (separate) regression analyses:

• regression from pain onto fatigue tells us if \(a\) is significant;
• multiple linear regression from pain and fatigue onto well-being tells us if \(b\) and \(c\,'\) are significant;
• regression from pain onto well-being tells if \(c\) is significant and/or different from \(c\,'\).

Paths c’ and b in basic SPSS regression output

SPSS Regression Dialogs

So let's first run the regression analysis for effect \(a\) (X onto mediator) in SPSS: we'll open wellbeing.sav and navigate to the linear regression dialogs as shown below.

For a fairly basic analysis, we'll fill out these dialogs as shown below.

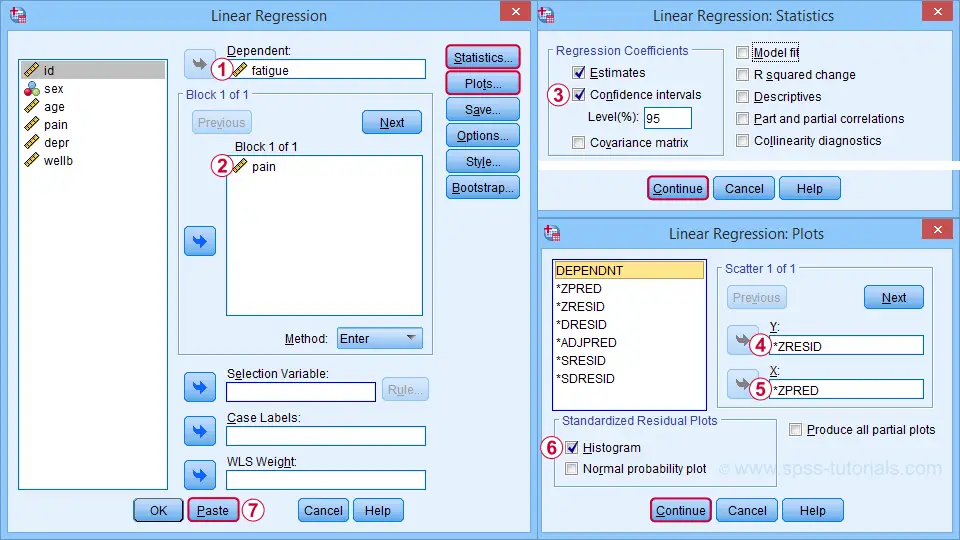
Completing these steps results in the SPSS syntax below. I suggest you shorten the pasted version a bit.

A second regression analysis estimates effects \(b\) and \(c\,'\). The easiest way to run it is to copy, paste and edit the first syntax as shown below.

We'll use the syntax below for the third (and final) regression which estimates \(c\), the total effect.

SPSS Mediation Analysis Output

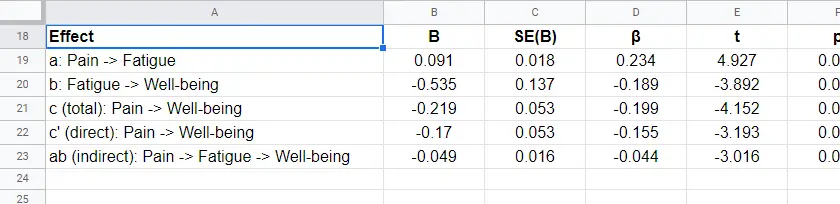
For our mediation analysis, we really only need the 3 coefficients tables. I copy-pasted them into this Googlesheet (read-only, partly shown below).

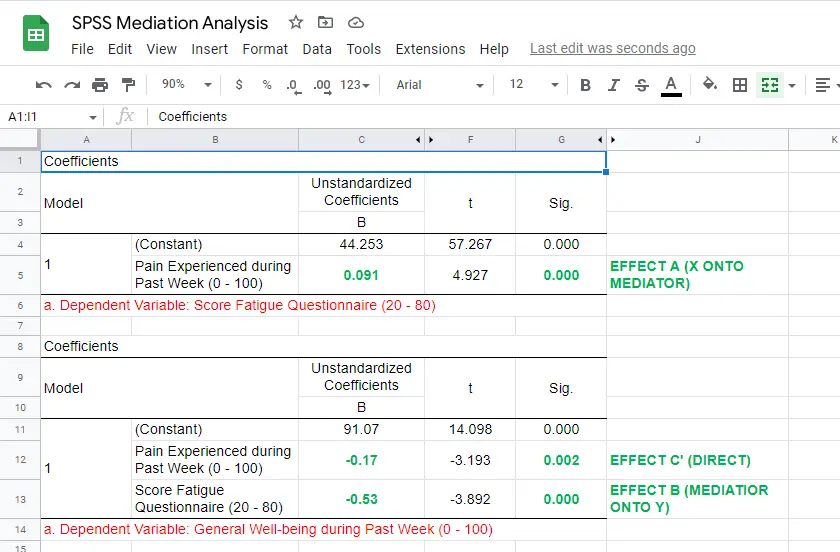
So what do we conclude? Well, all requirements for mediation are met by our results:

• effects \(a\), \(b\) and \(c\) are all statistically significant. This is because their “Sig.” or p < .05;
• the direct effect \(c\,'\) = -0.17 and thus closer to zero than the total effect \(c\) = -0.22.

The diagram below summarizes these results.

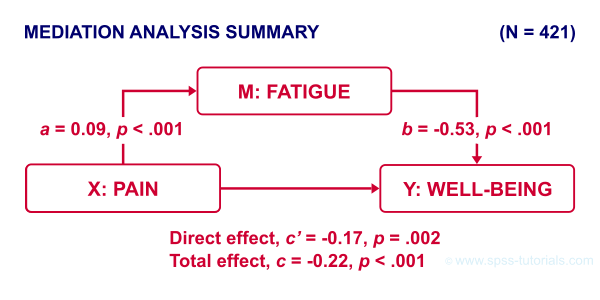
Note that both \(c\) and \(c\,'\) are significant. This is often called partial mediation: fatigue partially mediates the effect from pain onto well-being: adding it decreases the effect but doesn't nullify it altogether.

Besides partial mediation, we sometimes find full mediation. This means that \(c\) is significant but \(c\,'\) isn't: the effect is fully mediated and thus disappears when the mediator is added to the regression model.

APA Reporting Mediation Analysis

Mediation analysis is often reported as separate regression analyses as in “the first step of our analysis showed that the effect of pain on fatigue was significant, b = 0.09, p < .001...” Some authors also include t-values and degrees of freedom (df) for b-coefficients. For some very dumb reason, SPSS does not report degrees of freedom but you can compute them as

$$df = N - k - 1$$

where

• \(N\) denotes the total sample size (N = 421 in our example) and
• \(k\) denotes the number of predictors in the model (1 or 2 in our example).

Like so, we could report “the second step of our analysis showed that the effect of fatigue on well-being was also significant, b = -0.53, t(419) = -3.89, p < .001...”

Next Steps - The Sobel Test

In our analysis, the indirect effect of pain via fatigue onto well-being consists of two separate effects, \(a\) (pain onto fatigue) and \(b\) fatigue onto well-being. Now, the entire indirect effect \(ab\) is simply computed as

$$\text{indirect effect} \;ab = a \cdot b$$

This makes perfect sense: if wage \(a\) is $30 per hour and tax \(b\) is $0.20 per dollar income, then I'll pay $30 · $0.20 = $6.00 tax per hour, right?

For our example, \(ab\) = 0.09 · -0.53 = -0.049: for every unit increase in pain, well-being decreases by an average 0.049 units via fatigue. But how do we obtain the p-value and confidence interval for this indirect effect? There's 2 basic options:

• the modern literature favors bootstrapping as implemented in the PROCESS macro which we'll discuss later;
• the Sobel test (also known as “normal theory” approach).

The second approach assumes \(ab\) is normally distributed with

$$se_{ab} = \sqrt{a^2se^2_b + b^2se^2_a + se^2_a se^2_b}$$

where

\(se_{ab}\) denotes the standard error of \(ab\) and so on.

For the actual calculations, I suggest you try our Sobel Test Calculator.xlsx, partly shown below.

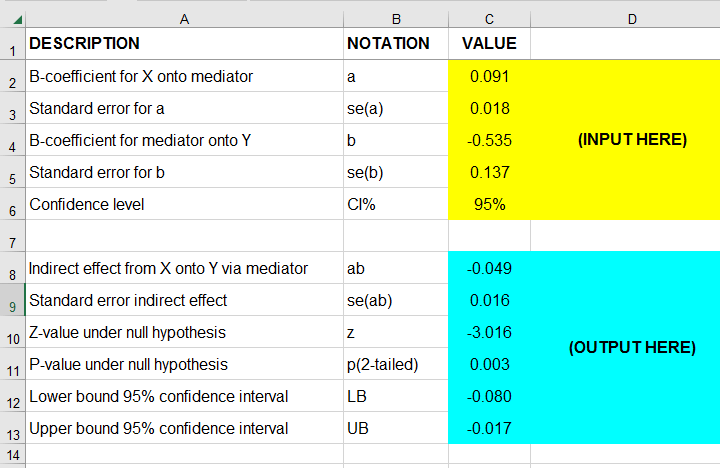
So what does this tell us? Well, our indirect effect is significant, B = -0.049, p = .002, 95% CI [-0.08, -0.02].

Next Steps - Index of Mediation

Our research variables (such as pain & fatigue) were measured on different scales without clear units of measurement. This renders it impossible to compare their effects. The solution is to report standardized coefficients known as β (Greek letter “beta”).

Our SPSS output already includes beta for most effects but not for \(ab\). However, we can easily compute it as

$$\beta_{ab} = \frac{ab \cdot SD_x}{SD_y}$$

where

\(SD_x\) is the sample-standard-deviation of our X variable and so on.

This standardized indirect effect is known as the index of mediation. For computing it, we may run something like DESCRIPTIVES pain wellb. in SPSS. After copy-pasting the resulting table into this Googlesheet, we'll compute \(\beta_{ab}\) with a quick formula as shown below.

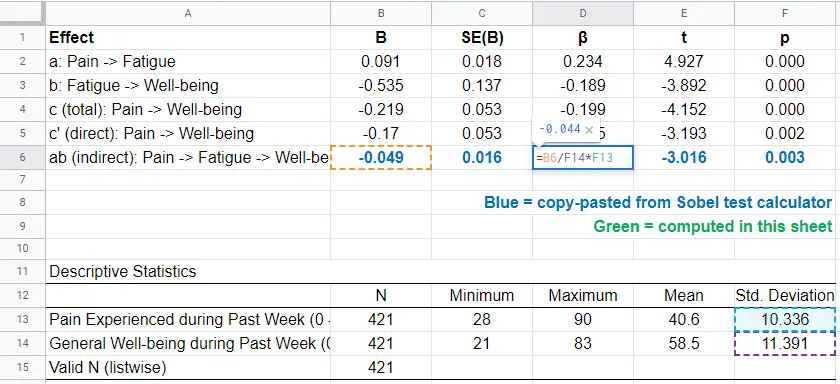
Adding the output from our Sobel test calculator to this sheet results in a very complete and clear summary table for our mediation analysis.

Final Notes

Mediation analysis in SPSS can be done with or without the PROCESS macro. Some reasons for not using PROCESS are that

• many people find PROCESS difficult to use and dislike its output format;
• PROCESS can't create regression residuals and the associated plots for checking regression assumptions such as linearity, homoscedasticity and normality;
• the PROCESS output does not include adjusted r-squared;
• PROCESS does not offer pairwise exclusion of missing values.

So why does anybody use PROCESS? Some reasons may be that

• PROCESS uses bootstrapping rather than the Sobel test. This is said to result in higher power and more accurate confidence intervals. Sadly, bootstrapping does not yield a p-value for the indirect effect whereas the Sobel test does;
• using PROCESS may save a lot of work for more complex models (parallel, serial and moderated mediation);
• if needed, PROCESS handles dummy coding for the X variable and moderators (if any);
• PROCESS doesn't require the additional calculations that we implemented in our Googlesheet: it calculates everything you need in one go.

Right. I hope this tutorial has been helpful for running, reporting and understanding mediation analysis in SPSS. This is perhaps not the easiest topic but remember that practice makes perfect.

Thanks for reading!

SPSS Mediation Analysis with PROCESS

• SPSS PROCESS Dialogs
• SPSS PROCESS Output
• Mediation Summary Diagram & Conclusion
• Indirect Effect and Index of Mediation
• APA Reporting Mediation Analysis

Introduction

A study investigated general well-being among a random sample of N = 421 hospital patients. Some of these data are in wellbeing.sav, partly shown below.

One investigator believes that

• pain increases fatigue and
• fatigue -in turn- decreases overall well-being.

That is, the relation from pain onto well-being is thought to be mediated by fatigue, as visualized below (top half).

Besides this indirect effect through fatigue, pain could also directly affect well-being (top half, path \(c\,'\)).

Now, what would happen if this model were correct and we'd (erroneously) leave fatigue out of it? Well, in this case the direct and indirect effects would be added up into a total effect (path \(c\), lower half). If all these hypotheses are correct, we should see the following in our data:

• assuming sufficient sample size, paths \(a\) and \(b\) should both be significant;
• path \(c\,'\) (direct effect) should be different from \(c\) (total effect).

One approach to such a mediation analysis is a series of (linear) regression analyses as discussed in SPSS Mediation Analysis Tutorial. An alternative, however, is using the SPSS PROCESS macro as we'll demonstrate below.

Quick Data Checks

Rather than blindly jumping into some advanced analyses, let's first see if our data look plausible in the first place. As a quick check, let's inspect the histograms of all variables involved. We'll do so from the SPSS syntax below. For more details, consult Creating Histograms in SPSS.

Result

First off, note that all variables have N = 421 so there's no missing values. This is important to make sure because PROCESS can only handle cases that are complete on all variables involved in the analysis.

Second, there seem to be some slight outliers. This especially holds for fatigue as shown below.

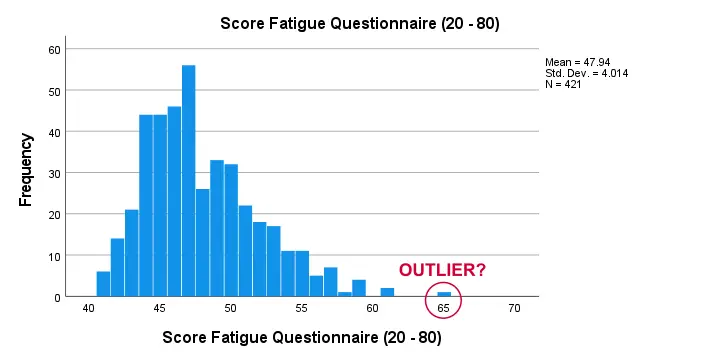
I think these values still look pretty plausible and I don't expect them to have a major impact on our analyses. Although disputable, I'll leave them in the data for now.

SPSS PROCESS Dialogs

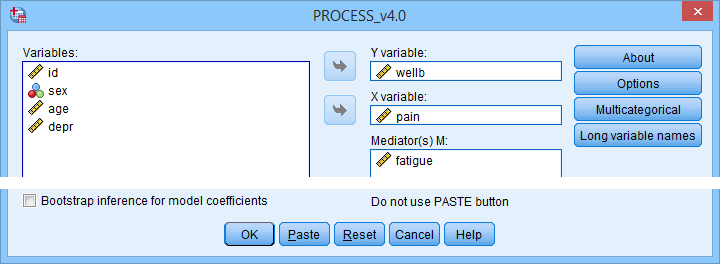
First off, make sure you have PROCESS installed as covered in SPSS PROCESS Macro Tutorial. After opening our data in SPSS, let's navigate to Analyze Regression PROCESS v4.2 by Andrew F. Hayes as shown below.

For a simple mediation analysis, we fill out the PROCESS dialogs as shown below.

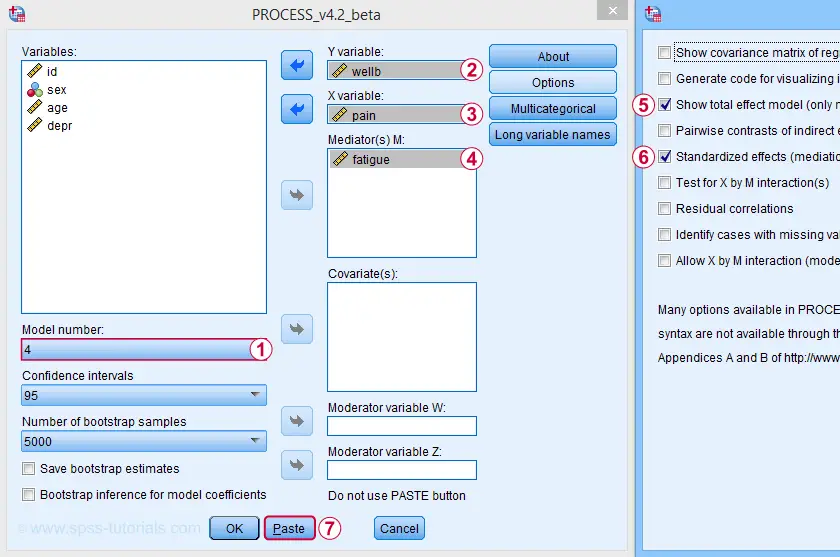
After completing these steps, you can either

• click “Ok” and just run the analysis;
• click “Paste” and run the (huge) syntax that's pasted or;
• click “Paste”, rearrange the syntax and then run it.

We discussed this last option in SPSS PROCESS Macro Tutorial. This may take you a couple of minutes but it'll pay off in the end. Our final syntax is shown below.

SPSS PROCESS Output

Let's first look at path \(a\): this is the effect from \(X\) (pain) onto \(M\) (fatigue). We find it in the output if we look for OUTCOME VARIABLE fatigue as shown below.

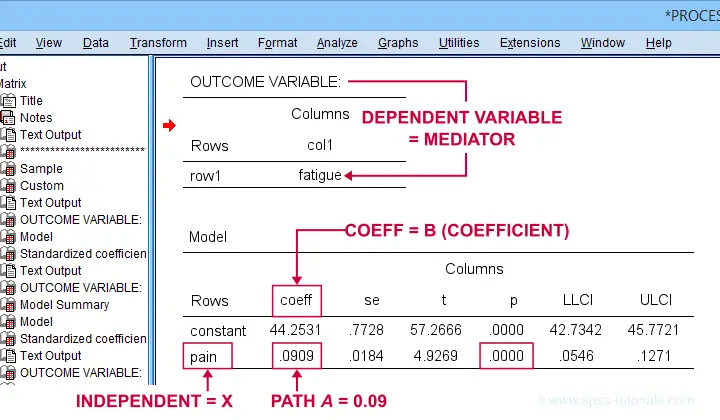
For path \(a\), b = 0.09, p < .001: on average, higher pain scores are associated with more fatigue and this is highly statistically significant. This outcome is as expected if our mediation model is correct.

SPSS PROCESS Output - Paths B and C’

Paths \(b\) and \(c\,'\) are found in a single table. It's the one for which OUTCOME VARIABLE is \(Y\) (well-being) and includes b-coefficients for both \(X\) (pain) and \(M\) fatigue.

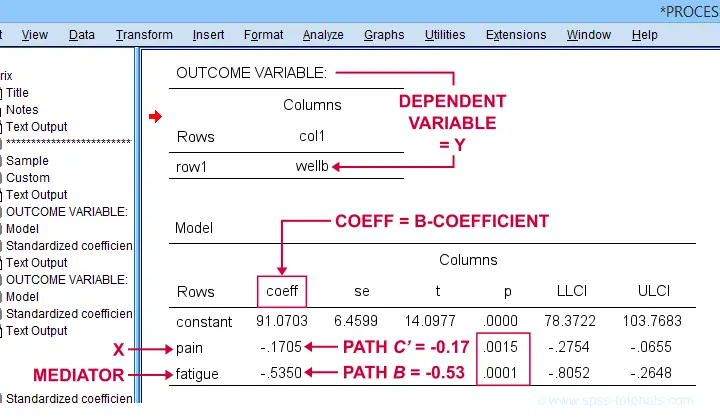
Note that path \(b\) is highly significant, as expected from our mediation hypotheses. Path \(c\,'\) (the direct effect) is also significant but our mediation model does not require this.

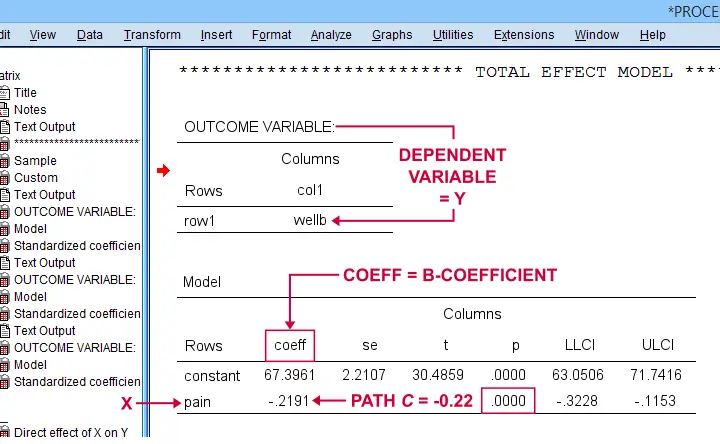
SPSS PROCESS Output - Path C

Some (but not all) authors also report the total effect, path \(c\). It is found in the table that has OUTCOME VARIABLE \(Y\) (well-being) that does not have a b-coefficient for the mediator.

Mediation Summary Diagram & Conclusion

The 4 main paths we examined thus far suffice for a classical mediation analysis. We summarized them in the figure below.

As hypothesized, paths \(a\) and \(b\) are both significant. Also note that direct effect is closer to zero than the total effect. This makes sense because the (negative) direct effect is the (negative) total effect minus the (negative) indirect effect.

A final point is that the direct effect is still significant: the indirect effect only partly accounts for the relation from pain onto well-being. This is known as partial mediation. A careful conclusion could thus be that the effect from pain onto well-being
is partially mediated by fatigue.

Indirect Effect and Index of Mediation

Thus far, we established mediation by examining paths \(a\) and \(b\) separately. A more modern approach, however, focuses mostly on the entire indirect effect which is simply

$$\text{indirect effect } ab = a \cdot b$$

For our example, \(ab\) is the change in \(Y\) (well-being) associated with a 1-unit increase in \(X\) pain through \(M\) (fatigue). This indirect effect is shown in the table below.

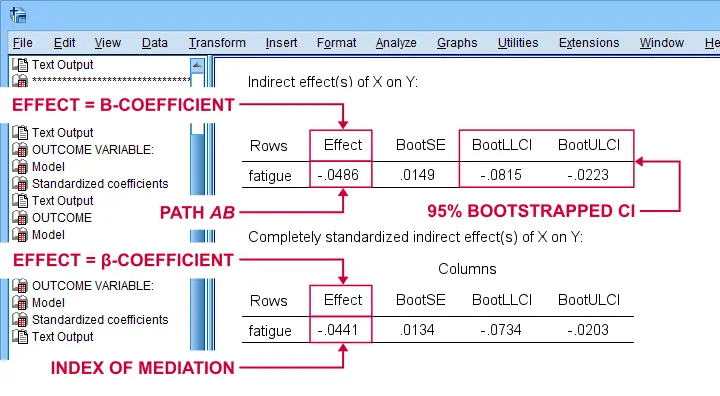
Note that PROCESS does not compute any p-value or confidence interval (CI) for \(ab\). Instead, it estimates a CI by bootstrapping. This CI may be slightly different in your output because it's based on random sampling.

Importantly, the 95% CI [-0.08, -0.02] does not contain zero. This tells us that p < .05 even though we don't have an exact p-value. An alternative for bootstrapping that does come up with a p-value here is the Sobel test.

PROCESS also reports the standardized b-coefficient for \(ab\). This is usually denoted as β and is completely unrelated to (1 - β) or power in statistics. This number, 0.04, is known as the index of mediation and is often interpreted as an effect size measure.

A huge stupidity in this table is that b is denoted as “Effect” rather than “coeff” as in the other tables. For adding to the confusion, “Effect” refers to either b or β. Denoting b as b and β as β would have been highly preferable here.

APA Reporting Mediation Analysis

Mediation analysis is often reported as separate regression analyses: “the first step of our analysis showed that the effect of pain on fatigue was significant, b = 0.09, p < .001...” Some authors also include t-values and degrees of freedom (df) for b-coefficients. For some dumb reason, PROCESS does not report degrees of freedom but you can compute them as

$$df = N - k - 1$$

where

• \(N\) denotes the total sample size (N = 421 in our example) and
• \(k\) denotes the number of predictors in the model (1 or 2 in our example).

Like so, we could report “the second step of our analysis showed that the effect of fatigue on well-being was also significant, b = -0.53, t(419) = -3.89, p < .001...”

Final Notes

First off, mediation is inherently a causal model: \(X\) causes \(M\) which, in turn, causes \(Y\). Nevertheless, mediation analysis does not usually support any causal claims. A rare exception could be \(X\) being a (possibly dichotomous) manipulation variable. In most cases, however, we can merely conclude that our data do (not) contradict
some (causal) mediation model. This is not quite the strong conclusion we'd usually like to draw.

A second point is that I dislike the verbose text reporting suggested by the APA. As shown below, a simple table presents our results much more clearly and concisely.

Lastly, we feel that our example analysis would have been stronger if we had standardized all variables into z-scores prior to running PROCESS. The simple reason is that unstandardized values are uninterpretable for variables such as pain, fatigue and so on. What does a pain score of 60 mean? Low? Medium? High?

In contrast: a pain z-score of -1 means one standard deviation below the mean. If these scores are normally distributed, this is roughly the 16th percentile.

This point carries over to our regression coefficients: b-coefficients are not interpretable because
we don't know how much a “unit” is for our (in)dependent variables. Therefore, reporting only β coefficients makes much more sense.

Now, we do have these standardized coefficients in our output. However, most confidence intervals apply to the unstandardized coefficients. This can be fixed by standardizing all variables prior to running PROCESS.

Thanks for reading!

SPSS PROCESS Macro Tutorial

• Downloading & Installing PROCESS
• Creating Tables instead of Text Output
• Using PROCESS with Syntax
• PROCESS Model Numbers
• PROCESS & Dummy Coding
• Strengths & Weaknesses of PROCESS

What is PROCESS?

PROCESS is a freely downloadable SPSS tool for estimating regression models with mediation and/or moderation effects. An example of such a model is shown below.

This model can fairly easily be estimated without PROCESS as discussed in SPSS Mediation Analysis Tutorial. However, using PROCESS has some advantages (as well as disadvantages) over a more classical approach. So how to get PROCESS and how does it work?

Those who want to follow along may download and open wellbeing.sav, partly shown below.

Note that this tutorial focuses on becoming proficient with PROCESS. The example analysis will be covered in a future tutorial.

Downloading & Installing PROCESS

PROCESS can be downloaded here (scroll down to “PROCESS macro for SPSS, SAS, and R”). The download comes as a .zip file which you first need to unzip. After doing so, in SPSS, navigate to Extensions Utilities Install Custom Dialog (Compatibility Mode) Select “process.spd” and click “Open” as shown below.

This should work for most SPSS users on recent versions. If it doesn't, consult the installation instructions that are included with the download.

Running PROCESS

If you successfully installed PROCESS, you'll find it in the regression menu as shown below.

For a very basic mediation analysis, we fill out the dialog as shown below.

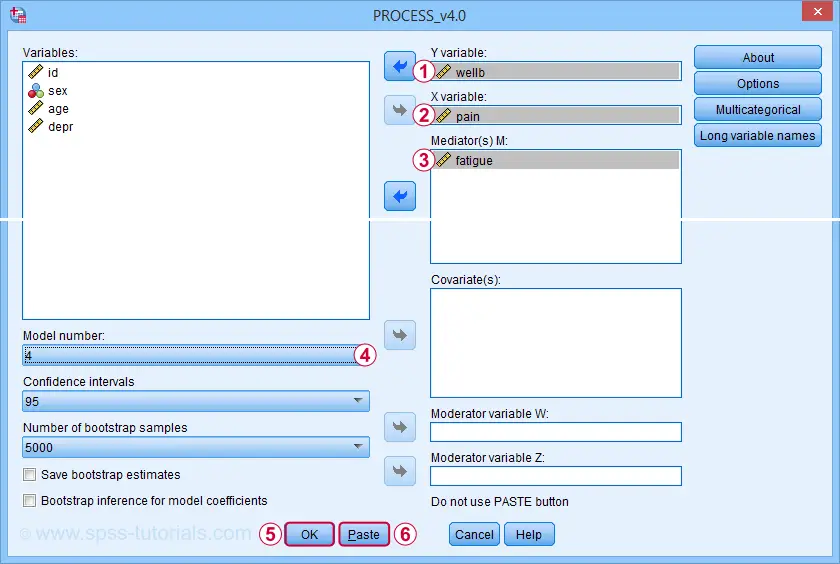
Y refers to the dependent (or “outcome”) variable;

X refers to the independent variable or “predictor” in a regression context;

For simple mediation, select model 4. We'll have a closer look at model numbers in a minute;

Just for now, let's click “Ok”.

Result

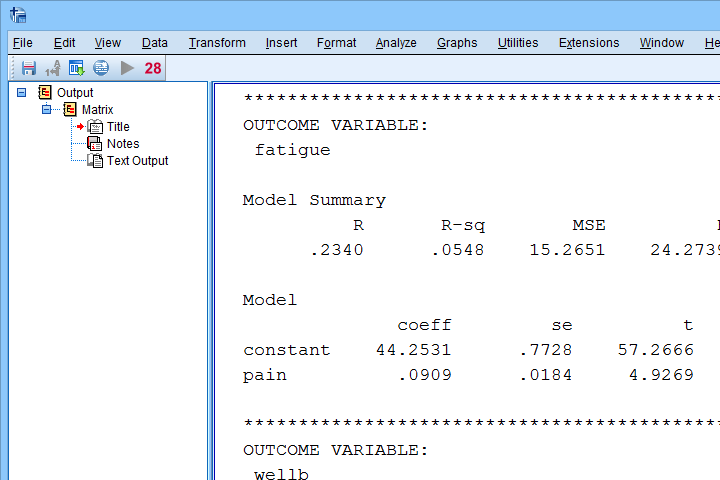
The first thing that may strike you, is that the PROCESS output comes as plain text. This is awkward because formatting it is very tedious and you can't adjust any decimal places. So let's fix that.

Creating Tables instead of Text Output

If you're using SPSS version 24 or higher, run the following SPSS syntax: set mdisplay tables. After doing so, running PROCESS will result in normal SPSS output tables rather than plain text as shown below.

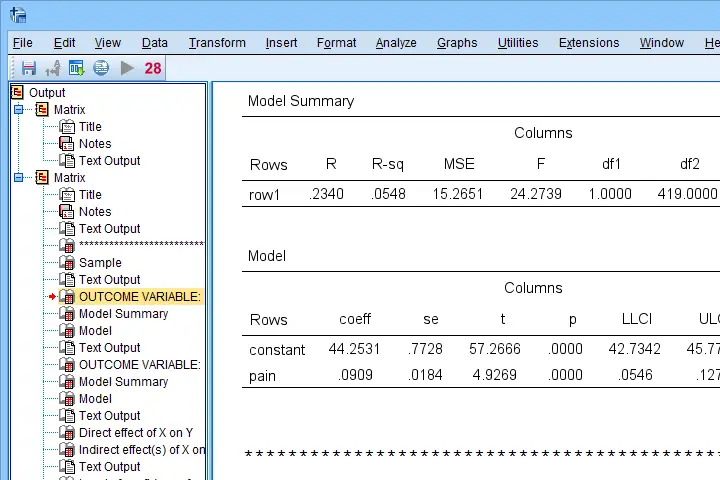
Note that you can readily copy-paste these tables into Excel and/or adjust their decimal places.

Using PROCESS with Syntax

First off: whatever you do in SPSS, save your syntax. Now, like any other SPSS dialog, PROCESS has a Paste button for pasting its syntax. However, a huge stupidity from the programmers is that doing so results in some 6,140 (!) lines of syntax. I'll add the first lines below.

You can run and save this syntax but having over 6,140 lines is awkward. Now, this huge syntax basically consists of 2 parts:

• a macro definition of some 6,130 lines: this consists of the formulas and computations that are performed on the input (variables, models and so on) that the SPSS user specifies;
• a macro call of some 10 lines: this tells SPSS to run the macro and which input to use.

The macro call is at the very end of the pasted syntax (use the Ctrl + End shortcut in your syntax window) and looks as follows.

After you run the (huge) macro definition just once during your session, you only need one (short) macro call for every PROCESS model you'd like to run.

A nice way to implement this, is to move the entire macro definition into a separate SPSS syntax file. Those who want to try this can download DEFINE-PROCESS-40.sps.

Although technically not mandatory, macro names should really start with exclamation marks. Therefore, we replaced DEFINE PROCESS with DEFINE !PROCESS in line 2,983 of this file. The final trick is that we can run this huge syntax file without opening it by using the INSERT command. Like so, the syntax below replicates our entire first PROCESS analysis.

Note: for replicating this, you may need to replace d:/downloaded by the folder where DEFINE-PROCESS-40.sps is located on your computer.

PROCESS Model Numbers

As we speak, PROCESS implements 94 models. An overview of the most common ones is shown in this Googlesheet (read-only), partly shown below.

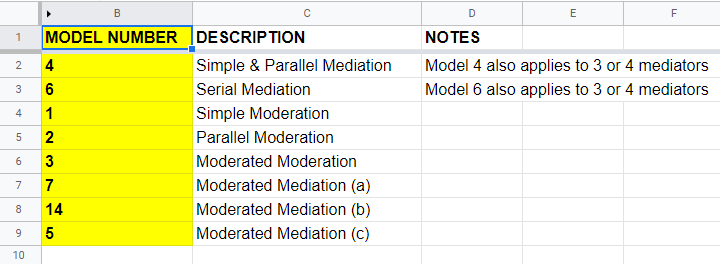
For example, if we have an X, Y and 2 mediator variables, we may hypothesize parallel mediation as illustrated below.

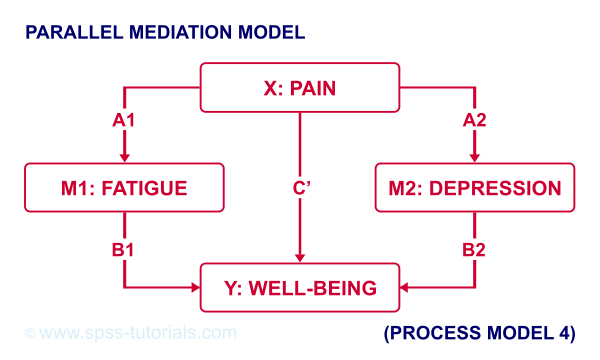
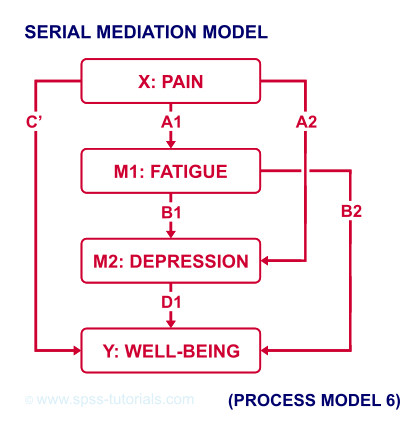
However, you could also hypothesize that mediator 1 affects mediator 2 which, in turn, affects Y. If you want to test this serial mediation effect, select model 6 in PROCESS.

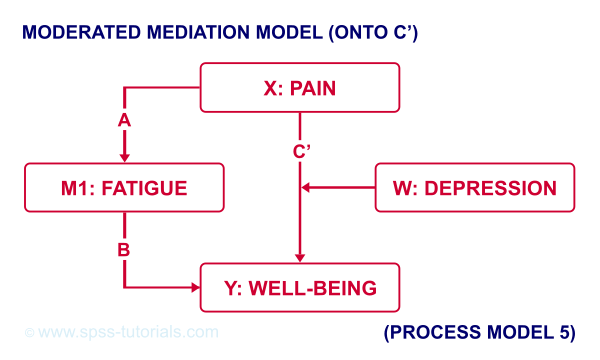
For moderated mediation, things get more complicated: the moderator could act upon any combination of paths a, b or c’. If you believe the moderator only affects path c’, choose model 5 as shown below.

An overview of all model numbers is given in this book.

PROCESS & Dummy Coding

A quick overview of variable types for PROCESS is shown in this Googlesheet (read-only), partly shown below.

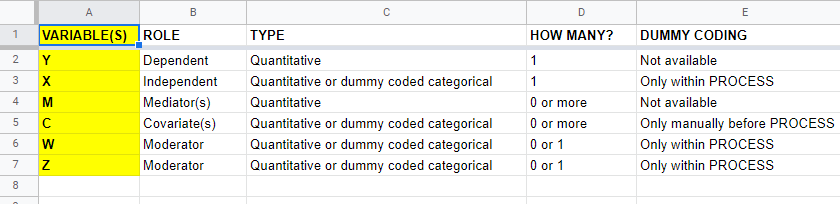
Keep in mind that PROCESS is entirely based on linear regression. This requires that dependent variables are quantitative (interval or ratio measurement level). This includes mediators, which act as both dependent and independent variables.

All other variables

• may be quantitative;
• may be dichotomous (preferably coded as 0-1);
• or must be dummy coded (nominal and ordinal variables).

X and moderator variables W and Z can only be dummy coded within PROCESS as shown below.

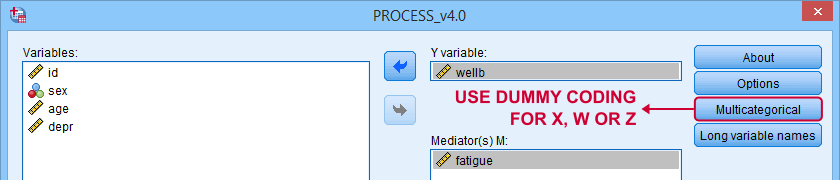
Covariates must be dummy coded before using PROCESS. For a handy tool, see SPSS Create Dummy Variables Tool.

Making Bootstrapping Replicable

Some PROCESS models rely on bootstrapping for reporting confidence intervals. Very basically, bootstrapping comes down to

• drawing a simple random sample (with replacement) from the data;
• computing statistics (for PROCESS, these are b-coefficients) on this new sample;
• repeating this procedure many (typically 1,000 - 10,000) times;
• examining to what extent each statistic fluctuates over these bootstrap samples.

Like so, a 95% bootstrapped CI for some parameter consists of the [2.5th - 97.5th] percentiles for some statistic over the bootstrap samples.

Now, due to the random nature of bootstrapping, running a PROCESS model twice typically results in slightly different CI's. This is undesirable but a fix is to add a /SEED subcommand to the macro call as shown below.

The random seed can be any positive integer. Personally, I tend to use the current date in YYYYMMDD format (20221227 is 27 December, 2022). An alternative is to run something like SET SEED 20221227. before running PROCESS. In this case, you need to prevent PROCESS from overruling this random seed, which you can do by replacing set seed = !seed. by *set seed = !seed. in line 3,022 of the macro definition.

Strengths & Weaknesses of PROCESS

A first strength of PROCESS is that it can save a lot of time and effort. This holds especially true for more complex models such as serial and moderated mediation.

Second, the bootstrapping procedure implemented in PROCESS is thought to have higher power and more accuracy than alternatives such as the Sobel test.

A weakness, though, is that PROCESS does not generate regression residuals. These are often used to examine model assumptions such as linearity and homoscedasticity as discussed in Linear Regression in SPSS - A Simple Example.

Another weakness of PROCESS is that some very basic models are not possible at all in PROCESS. A simple example is parallel moderation as illustrated below.

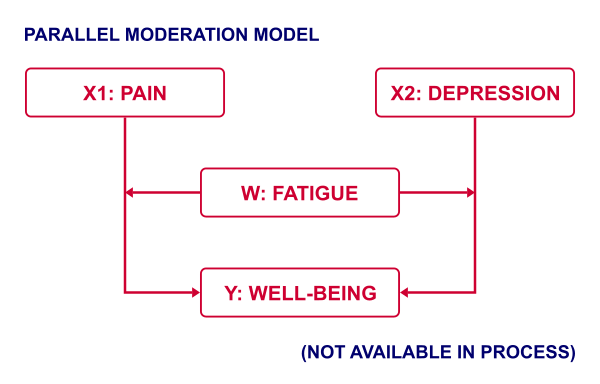
This can't be done because PROCESS is limited to a single X variable. Using just SPSS, estimating this model is a piece of cake. It's a tiny extension of the model discussed in SPSS Moderation Regression Tutorial.

A technical weakness is that PROCESS generates over 6,000 lines of syntax when pasted. The reason this happens is that PROCESS is built on 2 long deprecated SPSS techniques:

• the front end is an SPSS custom dialog (.spd) file. These have long been replaced by SPSS extension bundles (.spe files);
• the actual syntax is wrapped into a macro. SPSS macros have been deprecated in favor of Python ages ago.

I hope this will soon be fixed. There's really no need to bother SPSS users with 6,000 lines of source code.

Thanks for reading!

Sobel Test Tutorial & Calculator

The Sobel test is a significance test for indirect effects
in mediation analysis.

• Sobel Test Example
• Sobel Test - Formulas
• Sobel Test Excel Calculator
• Sobel Test Versus Bootstrapping
• Sobel Test in PROCESS Macro

Sobel Test Example

The diagram below summarizes some basic results discussed in SPSS Mediation Analysis Tutorial.

First off, note that

• path \(a\) from \(X\) onto \(M\) is statistically significant, b = 0.09, p < .001;
• path \(b\) from \(M\) onto \(Y\) is also “significant”, b = -0.53, p < .001.

Now, apart from these 2 components, what can we say about the entire indirect effect from \(X\) onto \(Y\) through \(M\)? Well, this is computed very simply as

$$\text{indirect effect} \;ab = a \cdot b$$

So for our example, that'll be

$$\text{indirect effect} \;ab = 0.09 \cdot -0.53 = -0.049$$

Note that this makes perfect sense. By analogy, if wage \(a\) is $30 per hour and tax \(b\) is $0.20 per dollar, then I'll pay $30 · $0.20 = $6.00 tax per hour.

Now, assuming our data are a random sample, we probably also want to know

• what's the p-value for the entire indirect effect \(ab\)?
• what's a confidence interval (CI) for \(ab\)?

One approach to both questions is the Sobel test. So how does it work?

Sobel Test - Formulas

First off, the Sobel test assumes that the sampling distribution for \(ab\) is a normal distribution with

$$se_{ab} = \sqrt{a^2se^2_b + b^2se^2_a + se^2_a se^2_b}$$

where

• \(se_{ab}\) denotes the standard error of \(ab\);
• \(a\) denotes path \(a\) (technically, a b-coefficient);
• \(se_a\) denotes the standard error of \(a\).

For our example, that'll be

$$se_{ab} = \sqrt{0.09^2 \cdot -0.14^2 + 0.53^2 \cdot 0.02^2 + 0.02^2 \cdot 0.14^2} = 0.016$$

For the actual calculations, I suggest you try our Sobel Test Calculator.xlsx, partly shown below.

So first our p-value: a likely null hypothesis is that \(\mu_{ab} = 0\) and therefore

$$Z_{ab} = \frac{ab - 0}{se_{ab}}$$

is assumed to follow the standard normal distribution.

For our example, that'll be

$$Z_{ab} = \frac{-0.049}{0.016} = 3.016$$

which results in p(2-tailed) = .003: our indirect effect is highly “significant”.

Second, our confidence interval: the alternative hypothesis is that \(\mu_{ab} = ab\) and therefore,

$$CI_{ab} = ab \pm z_{({1-^{\alpha}/_2})} \cdot se_{ab}$$

For our example, the 95% CI for \(ab\) would be roughly

$$CI_{ab} = -0.049 \pm 1.96 \cdot 0.016 = [-0.080, -0.017]$$

Sobel Test Excel Calculator

For quickly running one or many Sobel tests in applied research, I created Sobel Test Calculator.xlsx (partly shown below).

I prefer this over online calculators because

• I can easily copy-paste output from SPSS into this sheet;
• doing so is super precise because all decimal places are preserved (even though they're not shown);
• I can save this file with all input, output and formulas within my project archives so everything is accountable and replicable;
• for multiple Sobel tests, I can quickly and easily add some columns and duplicate parts of the input.

Sobel Test Versus Bootstrapping

For mediation analysis, bootstrapping is often preferred over the Sobel test because

• it's believed that \(ab\) is generally not exactly normally distributed, especially in smaller samples;
• bootstrapping is thought to have more power (that is, result in smaller CI's).

As a quick test, we also bootstrapped the indirect effect \(ab\) of our example analysis with the SPSS PROCESS macro. The bootstrapped sampling distribution over 5,000 bootstrap samples is shown below.

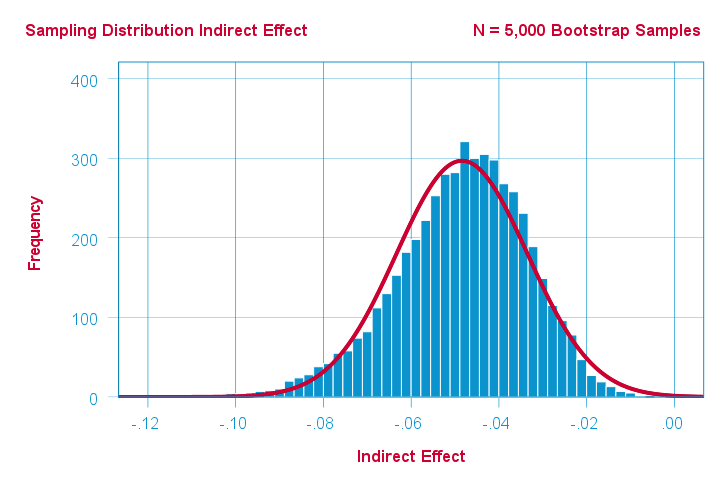
Indeed, this empirical distribution shows slight negative skewness. Nevertheless, it's reasonably normally distributed but this may be due to our pretty decent sample size of N = 421.

The bootstrapped 95% confidence interval is defined by the 2.5th and 97.5th percentiles of our 5,000 estimates for \(ab\). The PROCESS output is shown below.

Note that the bootstrapped CI is indeed slightly smaller than the one based on the Sobel test, which is [-0.080, -0.017].

Sobel Test in PROCESS Macro

The SPSS PROCESS macro computes the p-value but not the confidence interval for the Sobel test. This is done by adding /normal = 1 to the SPSS syntax for the macro call. This is because the Sobel test is also known as the normal theory test because it relies on \(ab\) being normally distributed.

Anyway. We used the syntax below but you'll probably want to consult SPSS PROCESS Macro Tutorial for replicating our analysis.

Result

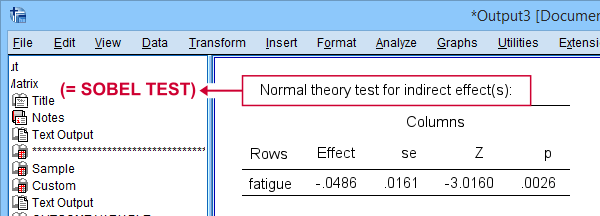
As shown, PROCESS comes up with the same results as our Excel calculator. For some dumb reason, however, it does not report the associated confidence interval for the indirect effect.

Right, I guess that should do regarding the Sobel test. I hope you found this tutorial and our calculator useful. If you've any questions or remarks, please throw us a comment below.

Thanks for reading!