SPSS ANCOVA – Beginners Tutorial
- ANCOVA - Null Hypothesis
- ANCOVA Assumptions
- SPSS ANCOVA Dialogs
- SPSS ANCOVA Output - Between-Subjects Effects
- SPSS ANCOVA Output - Adjusted Means
- ANCOVA - APA Style Reporting
A pharmaceutical company develops a new medicine against high blood pressure. They tested their medicine against an old medicine, a placebo and a control group. The data -partly shown below- are in blood-pressure.sav.
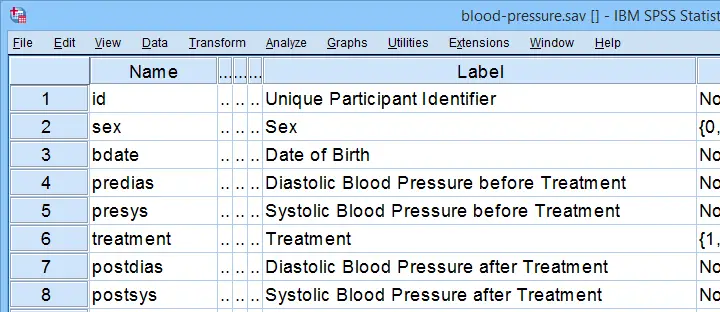
Our company wants to know if their medicine outperforms the other treatments: do these participants have lower blood pressures than the others after taking the new medicine? Since treatment is a nominal variable, this could be answered with a simple ANOVA.
Now, posttreatment blood pressure is known to correlate strongly with pretreatment blood pressure. This variable should therefore be taken into account as well. The relation between pretreatment and posttreatment blood pressure could be examined with simple linear regression because both variables are quantitative.
We'd now like to examine the effect of medicine while controlling for pretreatment blood pressure. We can do so by adding our pretest as a covariate to our ANOVA. This now becomes ANCOVA -short for analysis of covariance. This analysis basically combines ANOVA with regression.
Surprisingly, analysis of covariance does not actually involve covariances as discussed in Covariance - Quick Introduction.
ANCOVA - Null Hypothesis
Generally, ANCOVA tries to demonstrate some effect by rejecting the null hypothesis that all population means are equal when controlling for 1+ covariates. For our example, this translates to “average posttreatment blood pressures are equal for all treatments when controlling for pretreatment blood pressure”. The basic analysis is pretty straightforward but it does require quite a few assumptions. Let's look into those first.
ANCOVA Assumptions
- independent observations;
- normality: the dependent variable must be normally distributed within each subpopulation. This is only needed for small samples of n < 20 or so;
- homogeneity: the variance of the dependent variable must be equal over all subpopulations. This is only needed for sharply unequal sample sizes;
- homogeneity of regression slopes: the b-coefficient(s) for the covariate(s) must be equal among all subpopulations.
- linearity: the relation between the covariate(s) and the dependent variable must be linear.
Taking these into account, a good strategy for our entire analysis is to
- first run some basic data checks: histograms and descriptive statistics give quick insights into frequency distributions and sample sizes. This tells us if we even need assumptions 2 and 3 in the first place.
- see if assumptions 4 and 5 hold by running regression analyses for our treatment groups separately;
- run the actual ANCOVA and see if assumption 3 -if necessary- holds.
Data Checks I - Histograms
Let's first see if our blood pressure variables are even plausible in the first place. We'll inspect their histograms by running the syntax below. If you prefer to use SPSS’ menu, consult Creating Histograms in SPSS.
frequencies predias postdias
/format notable
/histogram.
Result
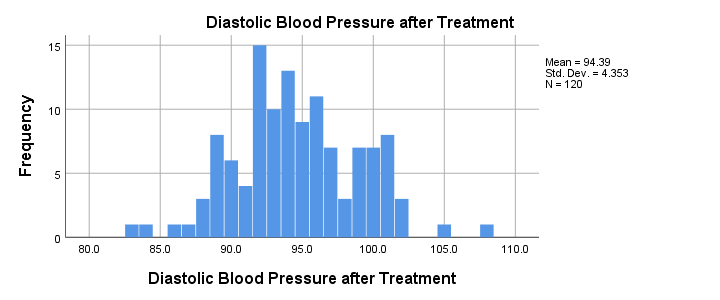
Conclusion: the frequency distributions for our blood pressure measurements look plausible: we don't see any very low or high values. Neither shows a lot of skewness or kurtosis and they both look reasonably normally distributed.
Data Checks II - Descriptive Statistics
Next, let's look into some descriptive statistics, especially sample sizes. We'll create and inspect a table with the
- sample sizes,
- means and
- standard deviations
of the outcome variable and the covariate for our treatment groups separately. We could do so from

 or -faster- straight from syntax.
or -faster- straight from syntax.
means predias postdias by treatment
/statistics anova.
Result
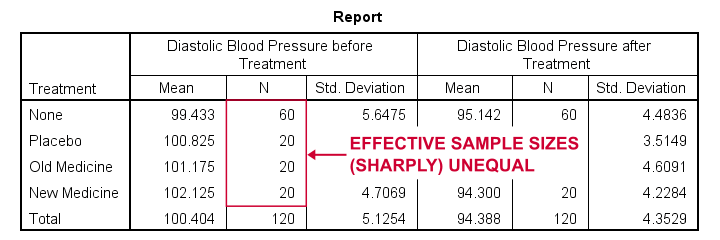
The main conclusions from our output are that
- all treatment groups have reasonable samples sizes of at least n = 20. This means we don't need to bother about the normality assumption. Otherwise, we could use a Shapiro-Wilk normality test or a Kolmogorov-Smirnov test but we rather avoid these.
- the treatment groups have sharply unequal sample sizes. This implies that our ANCOVA will need to satisfy the homogeneity of variance assumption.
- the ANOVA results (not shown here) tell us that the posttreatment means don't differ statistically significantly, F(3,116) = 1.619, p = 0.189. However, this test did not yet include our covariate -pretreatment blood pressure.
So much for our basic data checks. We'll now look into the regression results and then move on to the actual ANCOVA.
Separate Regression Lines for Treatment Groups
Let's now see if our regression slopes are equal among groups -one of the ANCOVA assumptions. We'll first just visualize them in a scatterplot as shown below.
Clicking results in the syntax below.
GRAPH
/SCATTERPLOT(BIVAR)=predias WITH postdias BY treatment
/MISSING=LISTWISE.GRAPH
/TITLE='Diastolic Blood Pressure by Treatment'.
*Double-click resulting chart and click "Add fit line at subgroups" icon.
SPSS now creates a scatterplot with different colors for different treatment groups. Double-clicking it opens it in a Chart Editor window. Here we click the “Add Fit Lines at Subgroups” icon as shown below.
Result
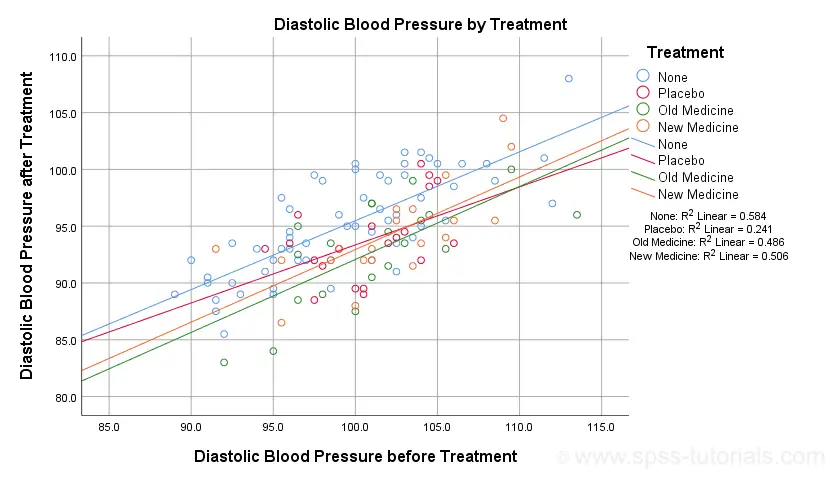
The main conclusion from this chart is that the regression lines are almost perfectly parallel: our data seem to meet the homogeneity of regression slopes assumption required by ANCOVA.
Furthermore, we don't see any deviations from linearity: this ANCOVA assumption also seems to be met. For a more thorough linearity check, we could run the actual regressions with residual plots. We did just that in SPSS Moderation Regression Tutorial.
Now that we checked some assumptions, we'll run the actual ANCOVA twice:
- the first run only examines the homogeneity of regression slopes assumption. If this holds, then there should not be any covariate by treatment interaction-effect.
- the second run tests our null hypothesis: are all population means equal when controlling for our covariate?
SPSS ANCOVA Dialogs
Let's first navigate to

 and fill out the dialog boxes as shown below.
and fill out the dialog boxes as shown below.
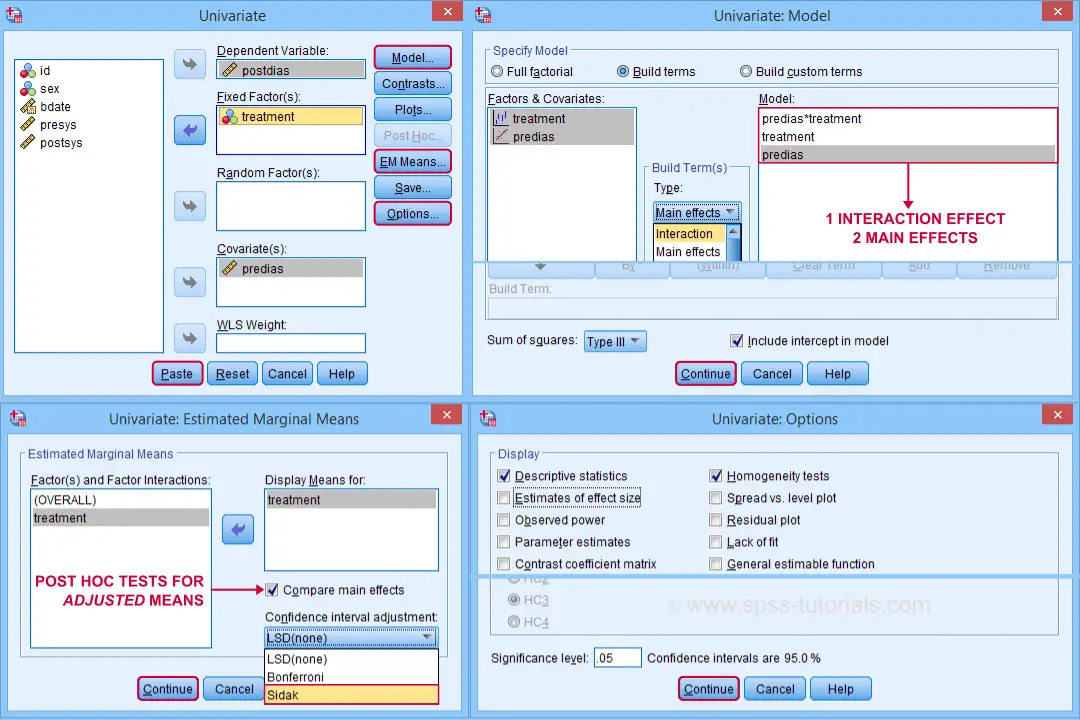
Clicking generates the syntax shown below.
UNIANOVA postdias BY treatment WITH predias
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/EMMEANS=TABLES(treatment) WITH(predias=MEAN) COMPARE ADJ(SIDAK)
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=predias treatment predias*treatment. /* predias*treatment adds interaction effect to model.
Result
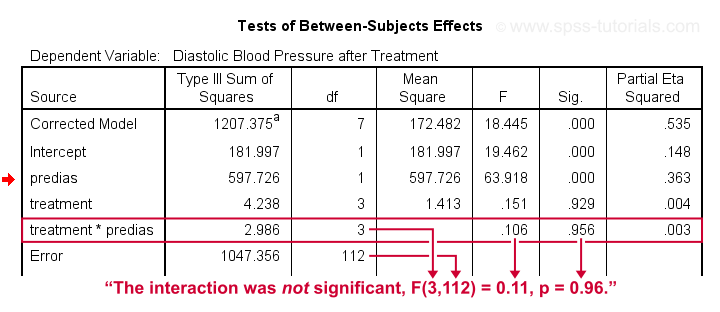
First note that our covariate by treatment interaction is not statistically significant at all: F(3,112) = 0.11, p = 0.96. This means that the regression slopes for the covariate don't differ between treatments: the homogeneity of regression slopes assumption seems to hold almost perfectly.
For these data, this doesn't come as a surprise: we already saw that the regression lines for different treatment groups were roughly parallel. Our first ANCOVA is basically a more formal way to make the same point.
SPSS ANCOVA II - Main Effects
We now run simply rerun our ANCOVA as previously. This time, however, we'll remove the covariate by treatment interaction effect. Doing so results in the syntax shown below.
UNIANOVA postdias BY treatment WITH predias
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/EMMEANS=TABLES(treatment) WITH(predias=MEAN) COMPARE ADJ(SIDAK)
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=predias treatment. /* only test for 2 main effects.
SPSS ANCOVA Output I - Levene's Test
Since our treatment groups have sharply unequal sample sizes, our data need to satisfy the homogeneity of variance assumption. This is why we included Levene's test in our analysis. Its results are shown below.

Conclusion: we don't reject the null hypothesis of equal error variances, F(3,116) = 0.56, p = 0.64. Our data meets the homogeneity of variances assumption. This means we can confidently report the other results.
SPSS ANCOVA Output - Between-Subjects Effects
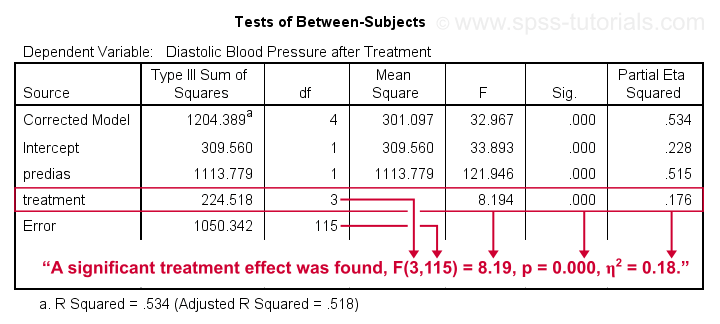
Conclusion: we reject the null hypothesis that our treatments result in equal mean blood pressures, F(3,115) = 8.19, p = 0.000.
Importantly, the effect size for treatment is between medium and large: partial eta squared (written as η2) = 0.176.
Apparently, some treatments perform better than others after all. Interestingly, this treatment effect was not statistically significant before including our pretest as a covariate.
So which treatments perform better or worse? For answering this, we first inspect our estimated marginal means table.
SPSS ANCOVA Output - Adjusted Means
One role of covariates is to adjust posttest means for any differences among the corresponding pretest means. These adjusted means and their standard errors are found in the Estimated Marginal Means table shown below.

These adjusted means suggest that all treatments result in lower mean blood pressures than “None”. The lowest mean blood pressure is observed for the old medicine. So precisely which mean differences are statistically significant? This is answered by post hoc tests which are found in the Pairwise Comparisons table (not shown here). This table shows that all 3 treatments differ from the control group but none of the other differences are statistically significant. For a more detailed discussion of post hoc tests, see SPSS - One Way ANOVA with Post Hoc Tests Example.
ANCOVA - APA Style Reporting
For reporting our ANCOVA, we'll first present descriptive statistics for
- our covariate;
- our dependent variable (unadjusted);
- our dependent variable (adjusted for the covariate).
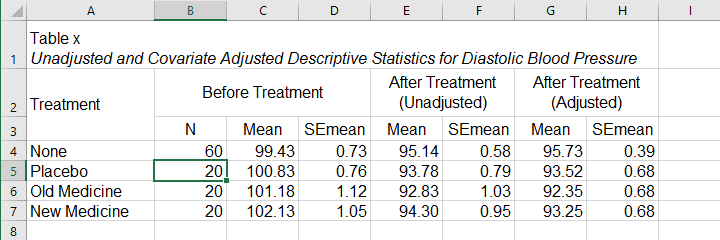
What's interesting about this table is that the posttest means are hardly adjusted by including our covariate. However, the covariate greatly reduces the standard errors for these means. This is why the mean differences are statistically significant only when the covariate is included. The adjusted descriptives are obtained from the final ANCOVA results. The unadjusted descriptives can be created from the syntax below.
means predias postdias by treatment
/cells count mean semean.
The exact APA table is best created by copy-pasting these statistics into Excel or Googlesheets.
Second, we'll present a standard ANOVA table for the effects included in our final model and error.
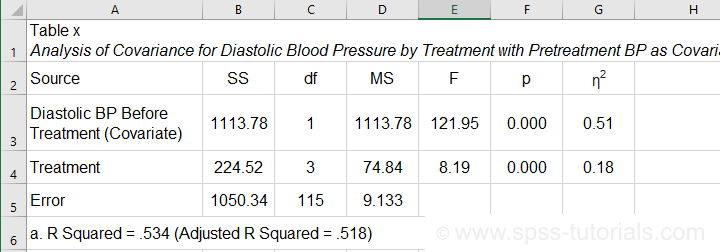
This table is constructed by copy-pasting the SPSS output table into Excel and removing the redundant rows.
Final Notes
So that'll do for a very solid but simple ANCOVA in SPSS. We could have written way more about this example analysis as there's much -much- more to say about the output. We'd also like to cover the basic ideas behind ANCOVA into more detail but that really requires a separate tutorial which we hope to write in some weeks from now.
Hope my tutorial has been helpful anyway. So last off:
thanks for reading!
SPSS ANOVA without Raw Data
- 1. Set Up Matrix Data File
- 2. SPSS Oneway Dialogs
- 3. Adjusting the Syntax
- 4. Interpreting the Output
In SPSS, you can fairly easily run an ANOVA or t-test without having any raw data. All you need for doing so are
- the sample sizes,
- the means and
- the standard deviations
of the dependent variable(s) for the groups you want to compare. This tutorial walks you through analyzing the journal table shown below.
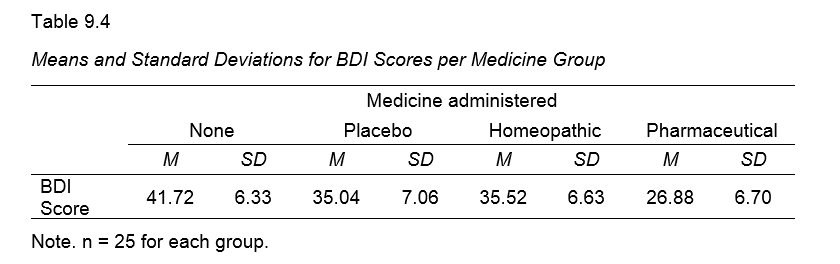
1. Set Up Matrix Data File
First off, we create an SPSS data file containing 3 rows for each group. You may use descriptives-for-anova-01.sav -partly shown below- as a starting point.
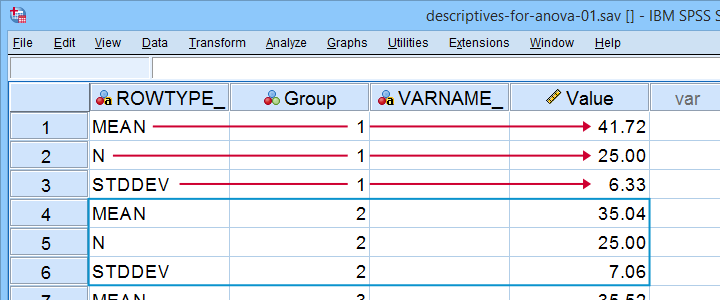
There's 3 adjustments you'll typically want to apply to this example data file:
- removing or adding sets of 3 rows if you want to compare fewer or more groups;
- changing sample sizes, means and standard deviations in the “Value” variable;
- changing the variable labels for the independent and dependent variables as indicated below.
I recommend you don't make any other changes to this data file or otherwise the final analysis is likely to crash. For instance,
- don't change any variable names;
- don't change the variable order;
- don't remove the empty string variable VARNAME_
2. SPSS Oneway Dialogs
First off, make sure the example data file is the only open data file in SPSS. Next, navigate to and fill out the dialogs as if you're analyzing a “normal” data file.
 You may select all options in this dialog. However, Levene's test -denoted as Homogeneity of variances test- will not run as it requires raw data.
You may select all options in this dialog. However, Levene's test -denoted as Homogeneity of variances test- will not run as it requires raw data.
This is no problem for the data at hand due to their equal sample sizes. For other data, it may be wise to carefully inspect the Welch test as discussed in SPSS ANOVA - Levene’s Test “Significant”.
Anyway, completing these steps results in the syntax below. But don't run it just yet.
ONEWAY Value BY Group
/ES=OVERALL
/STATISTICS DESCRIPTIVES WELCH
/PLOT MEANS
/MISSING ANALYSIS
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY ALPHA(0.05).
3. Adjusting the Syntax
Note that we created syntax just like we'd do when analyzing raw data. You could run it, but SPSS would misinterpret the data as 4 groups of 3 observations each. For SPSS to interpret our matrix data correctly, add /MATRIX IN(*). as shown below.
ONEWAY Value BY Group
/ES=OVERALL
/STATISTICS DESCRIPTIVES WELCH
/PLOT MEANS
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY ALPHA(0.05)
/matrix in(*).
*CORRECTED SYNTAX FOR SPSS 26 OR LOWER.
ONEWAY Value BY Group
/STATISTICS DESCRIPTIVES WELCH
/PLOT MEANS
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY ALPHA(0.05)
/matrix in(*).
4. Interpreting the Output
First off, note that SPSS has understood that our data file has 4 groups of 25 observations each as shown below.
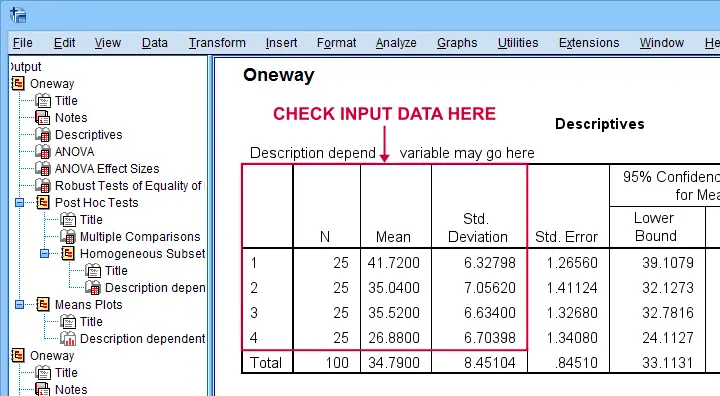
The remainder of the output is nicely detailed and includes
- the main ANOVA F-test;
- post-hoc tests (Tukey's HSD);
- the Welch test (not really needed for this example);
- a line chart visualizing our sample means;
- various effect size measures such as partial eta squared (only SPSS version 27+).
The main output you cannot obtain from these data are
- Levene's test for the homogeneity assumption;
- the Kolmogorov-Smirnov normality test and;
- the Shapiro-Wilk normality test.
For the sample sizes at hand, however, none of these are very useful anyway. A more thorough interpretation of the output for this analysis is presented in SPSS - One Way ANOVA with Post Hoc Tests Example.
Right, so I hope you found this tutorial helpful. We always appreciate if you throw us a quick comment below. Other that that:
Thanks for reading!
SPSS ANOVA – Levene’s Test “Significant”
An assumption required for ANOVA is homogeneity of variances. We often run Levene’s test to check if this holds. But what if it doesn't? This tutorial walks you through.
- SPSS ANOVA Dialogs I
- Results I - Levene’s Test “Significant“
- SPSS ANOVA Dialogs II
- Results II - Welch and Games-Howell Tests
- Plan B - Kruskal-Wallis Test
Example Data
All analyses in this tutorial use staff.sav, part of which is shown below. We encourage you to download these data and replicate our analyses.
Our data contain some details on a sample of N = 179 employees. The research question for today is: is salary associated with region? We'll try to support this claim by rejecting the null hypothesis that all regions have equal mean population salaries. A likely analysis for this is an ANOVA but this requires a couple of assumptions.
ANOVA Assumptions
An ANOVA requires 3 assumptions:
- independent observations;
- normality: the dependent variable must follow a normal distribution within each subpopulation.
- homogeneity: the variance of the dependent variable must be equal over all subpopulations.
With regard to our data, independent observations seem plausible: each record represents a distinct person and people didn't interact in any way that's likely to affect their answers.
Second, normality is only needed for small sample sizes of, say, N < 25 per subgroup. We'll inspect if our data meet this requirement in a minute.
Last, homogeneity is only needed if sample sizes are sharply unequal. If so, we usually run Levene's test. This procedure tests if 2+ population variances are all likely to be equal.
Quick Data Check
Before running our ANOVA, let's first see if the reported salaries are even plausible. The best way to do so is inspecting a histogram which we'll create by running the syntax below.
frequencies salary
/format notable
/histogram.
Result
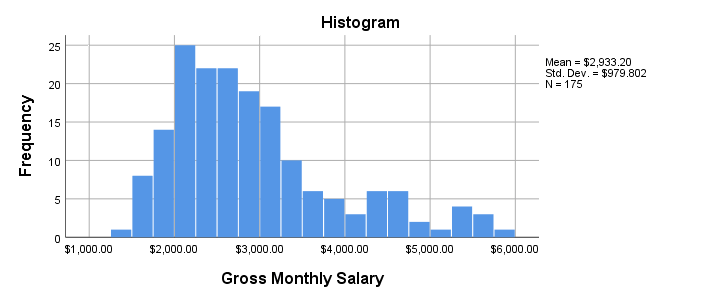
- Note that our histogram reports N = 175 rather than our N = 179 respondents. This implies that salary contains 4 missing values.
- The frequency distribution, however, looks plausible: there's no clear outliers or other abnormalities that should ring any alarm bells.
- The distribution shows some positive skewness. However, this makes perfect sense and is no cause for concern.
Let's now proceed to the actual ANOVA.
SPSS ANOVA Dialogs I
After opening our data in SPSS, let's first navigate to

 as shown below.
as shown below.
Let's now fill in the dialog that opens as shown below.
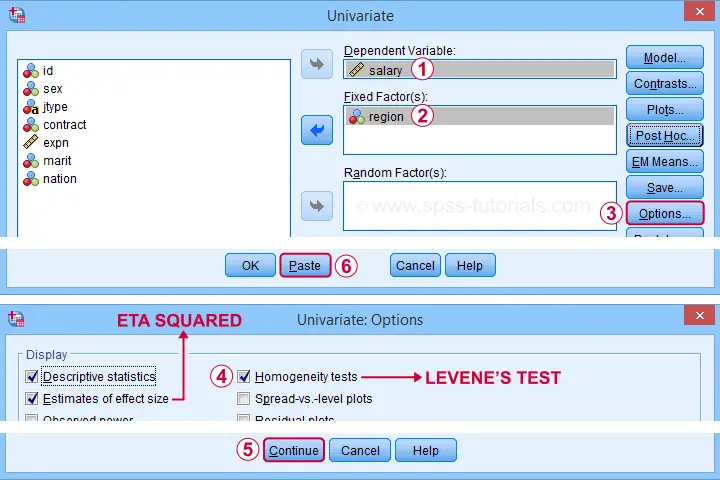
Completing these steps results in the syntax below. Let's run it.
UNIANOVA salary BY region
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT ETASQ DESCRIPTIVE HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=region.
Results I - Levene’s Test “Significant”
The very first thing we inspect are the sample sizes used for our ANOVA and Levene’s test as shown below.
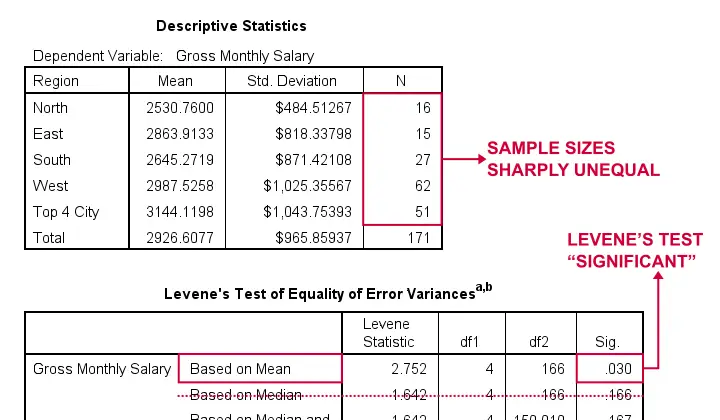
- First off, note that our Descriptive Statistics table is based on N = 171 respondents (bottom row). This is due to some missing values in both region and salary.
- Second, sample sizes for “North” and “East” are rather small. We may therefore need the normality assumption. For now, let's just assume it's met.
- Next, our sample sizes are sharply unequal so we really need to meet the homogeneity of variances assumption.
- However, Levene’s test is statistically significant because its p < 0.05: we reject its null hypothesis of equal population variances.
The combination of these last 2 points implies that we can not interpret or report the F-test shown in the table below.
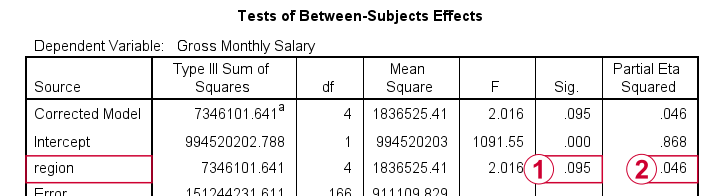
 As discussed, we can't rely on this p-value for the usual F-test.
As discussed, we can't rely on this p-value for the usual F-test.
 However, we can still interpret eta squared (often written as η2). This is a descriptive statistic that neither requires normality nor homogeneity. η2 = 0.046 implies a small to medium effect size for our ANOVA.
However, we can still interpret eta squared (often written as η2). This is a descriptive statistic that neither requires normality nor homogeneity. η2 = 0.046 implies a small to medium effect size for our ANOVA.
Now, if we can't interpret our F-test, then how can we know if our mean salaries differ? Two good alternatives are:
- running an ANOVA with the Welch statistic or
- a Kruskal-Wallis test.
Let's start off with the Welch statistic.
SPSS ANOVA Dialogs II
For inspecting the Welch statistic, first navigate to

 as shown below.
as shown below.
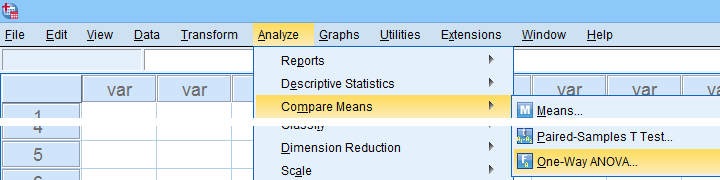
Next, we'll fill out the dialogs that open as shown below.
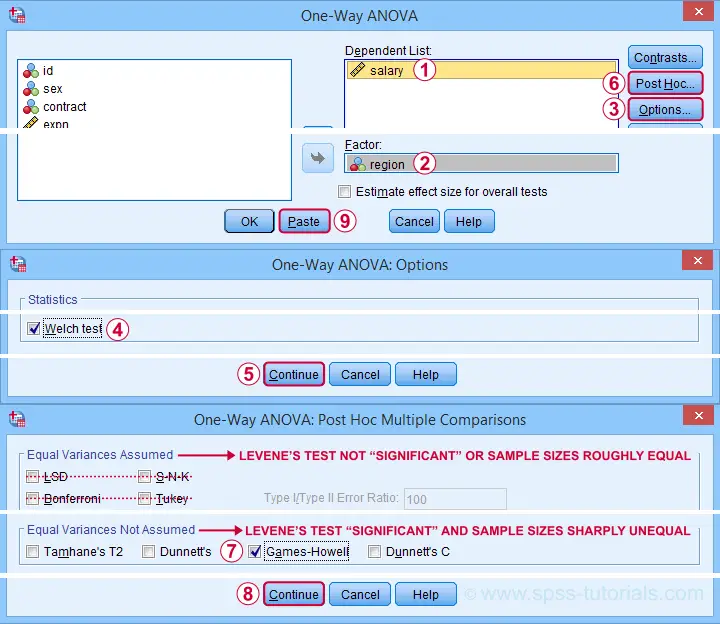
This results in the syntax below. Again, let's run it.
ONEWAY salary BY region
/STATISTICS HOMOGENEITY WELCH
/MISSING ANALYSIS
/POSTHOC=GH ALPHA(0.05).
Results II - Welch and Games-Howell Tests
As shown below, the Welch test rejects the null hypothesis of equal population means.

This table is labelled “Robust Tests...” because it's robust to a violation of the homogeneity assumption as indicated by Levene’s test. So we now conclude that mean salaries are not equal over all regions.
But precisely which regions differ with regard to mean salaries? This is answered by inspecting post hoc tests. And if the homogeneity assumption is violated, we usually prefer Games-Howell as shown below.
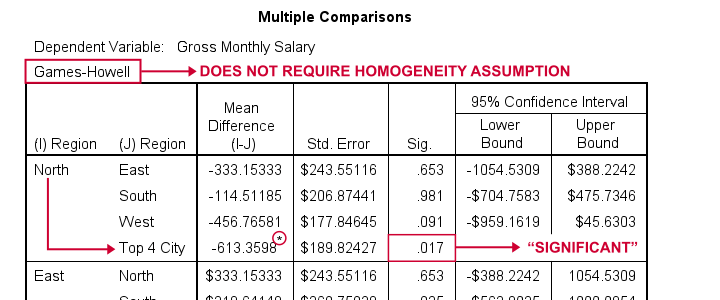
Note that each comparison is shown twice in this table. The only regions whose mean salaries differ “significantly” are North and Top 4 City.
Plan B - Kruskal-Wallis Test
So far, we overlooked one issue: some regions have sample sizes of n = 15 or n = 16. This implies that the normality assumption should be met as well. A terrible idea here is to run
for each region separately. Neither test rejects the null hypothesis of a normally distributed dependent variable but this is merely due to insufficient sample sizes.
A much better idea is running a Kruskal-Wallis test. You could do so with the syntax below.
NPAR TESTS
/K-W=salary BY region(1 5)
/STATISTICS DESCRIPTIVES
/MISSING ANALYSIS.
Result

Sadly, our Kruskal-Wallis test doesn't detect any difference between mean salary ranks over regions, H(4) = 6.58, p = 0.16.
In short, our analyses come up with inconclusive outcomes and it's unclear precisely why. If you've any suggestions, please throw us a comment below. Other than that,
Thanks for reading!
SPSS Two-Way ANOVA with Interaction Tutorial
Introduction & Practice Data File
Do you think running a two-way ANOVA with an interaction effect is challenging? Then this is the tutorial for you. We'll run the analysis by following a simple flowchart and we'll explain each step in simple language. After reading it, you'll know what to do and you'll understand why.
We'll use depression.sav throughout. The screenshot below shows it in variable view.
Research Questions
Very basically, 100 participants suffering from depression were divided into 4 groups of 25 each. Each group was given a different medicine. After 4 weeks, participants filled out the BDI, short for Beck's depression inventory. Our main research question is: did our different medicines result in different mean BDI scores? A secondary question is whether the BDI scores are related to gender in any way. In short we'll try to gain insight into 4 (medicines) x 2 (gender) = 8 mean BDI scores.
Quick Check: Histogram over Scores
Before jumping blindly into statistical tests, let's first see if our BDI scores make any sense in the first place. Before analyzing any metric variable, I always first inspect its histogram. The fastest way to create it is running the syntax below.
frequencies bdi
/format notable
/histogram.
Result
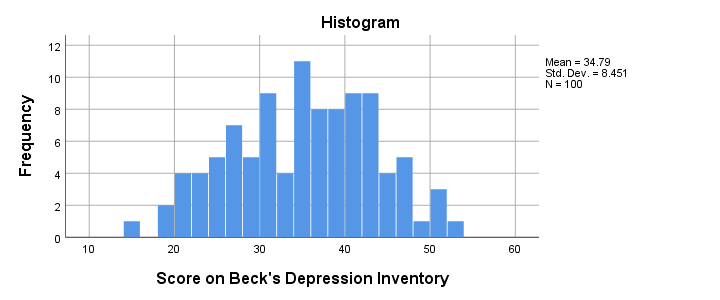
The scores look fine. We've perhaps one outlier who scores only 15 but we'll leave it in the data. The scores are roughly normally distributed and there's no need to specify any missing values.
ANOVA Assumptions
When we compare more than 2 means, we usually do so by ANOVA -short for analysis of variance. Doing so requires our data to meet the following assumptions:
- Independent observations (or independent and identically distributed variables). This often holds if each case contains a distinct person and the participants didn't interact.
- Homogeneity: the population variances are all equal over subpopulations. Violation of this assumption is less serious insofar as sample sizes are equal.
- Normality: the test variable must be normally distributed in each subpopulation. This assumption becomes less important insofar as the sample sizes are larger.
ANOVA Flowchart
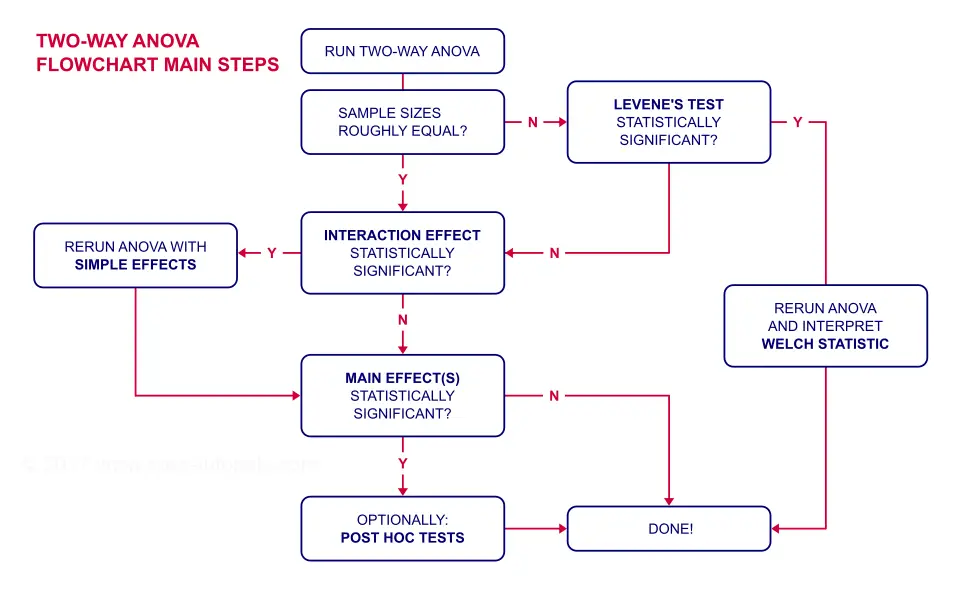
Inspecting Means and Sample Sizes
The first question in our ANOVA flowchart is whether the sample sizes are roughly equal. I like to run a means table for inspecting this because I'm going to need this table anyway for my report. I'll create it with the syntax below.
means bdi by gender by medicine
/cells count mean stddev.
*Note: MEANS allows you to choose exactly which statistics you want.
Result
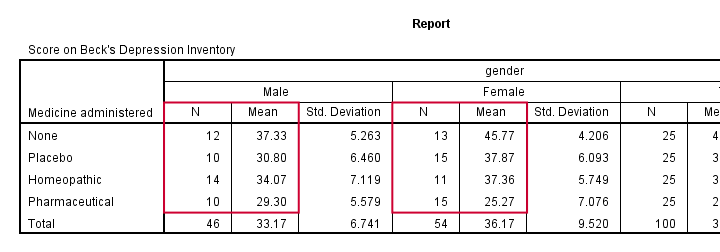
Note that this table shows the 8 means (2 genders * 4 medicines) that our analysis is all about. Each of these 8 means is based on 10 through 15 observations so the sample sizes are roughly equal.
This means that we don't need to bother about the homogeneity assumption. We can therefore skip Levene's test as shown in our flowchart.
Running Two-Way ANOVA in SPSS
We'll now run our two-way ANOVA through

 .
We'll then follow the screenshots below.
.
We'll then follow the screenshots below.
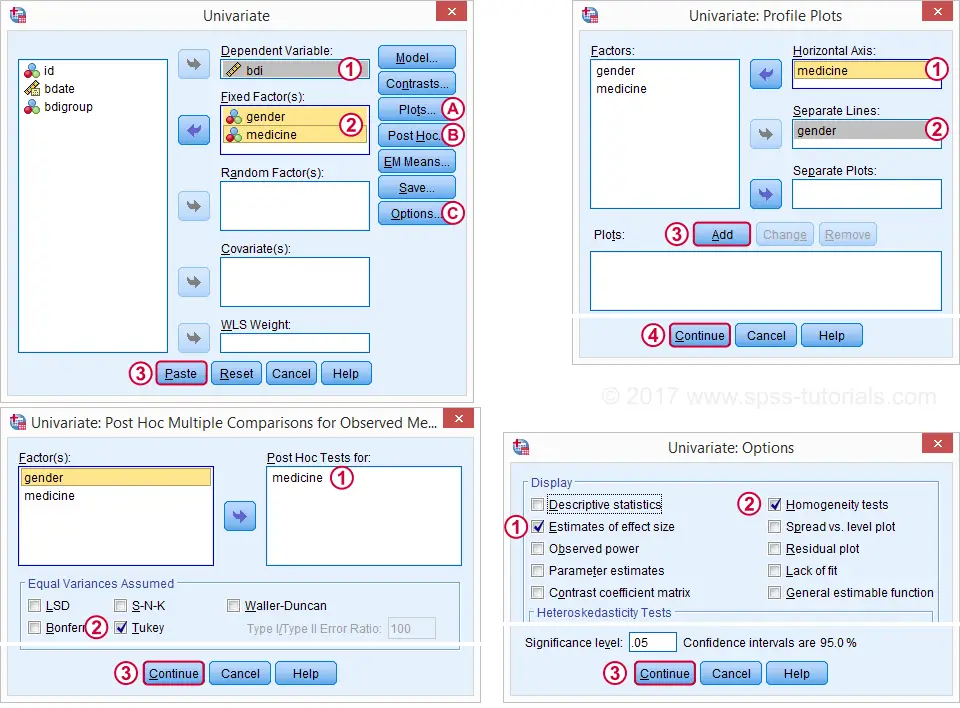
This results in the syntax below. Let's run it and see what happens.
UNIANOVA bdi BY gender medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PLOT=PROFILE(medicine*gender) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=gender medicine gender*medicine.
ANOVA Output - Between Subjects Effects
Following our flowchart, we should now find out if the interaction effect is statistically significant. A -somewhat arbitrary- convention is that an effect is statistically significant if “Sig.” < 0.05. According to the table below, our 2 main effects and our interaction are all statistically significant.
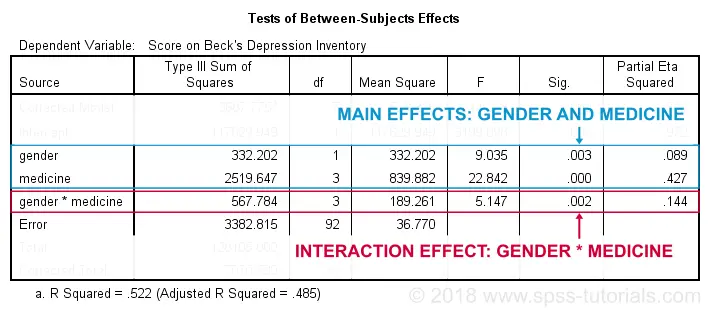
The flowchart says we should now rerun our ANOVA with simple effects. For now, we'll ignore the main effects -even if they're statistically significant. But why?! Well, this will become clear if we understand what our interaction effect really means. So let's inspect our profile plots.
ANOVA Output - Profile Plots
The profile plot shown below basically just shows the 8 means from our means table.If you ran the ANOVA like we just did, the “Estimated Marginal Means” are always the same as the observed means that we saw earlier. Interestingly, it also shows how medicine and gender affect these means.
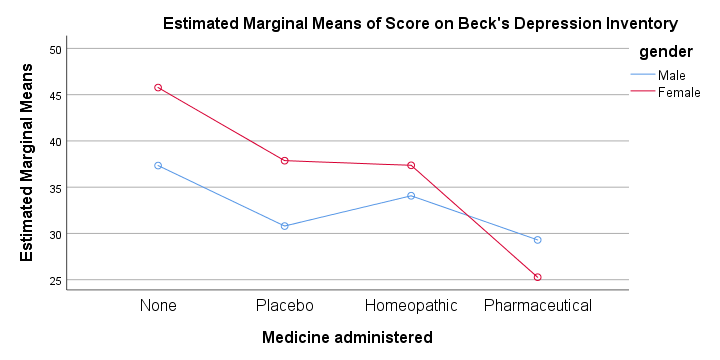
An interaction effect means that the effect of one factor depends on the other factor and it's shown by the lines in our profile plot not running parallel.
In this case, the effect for medicine interacts with gender. That is,
medicine affects females differently than males.
Roughly, we see the red line (females) descent quite steeply from “None” to “Pharmaceutical” whereas the blue line (males) is much more horizontal. Since it depends on gender,
there's no such thing as the effect of medicine.
So that's why we ignore the main effect of medicine -even if it's statistically significant. This main effect “lumps together” the different effects for males and females and this obscures -rather than clarifies- how medicine really affects the BDI scores.
Interaction Effect? Run Simple Effects.
So what should we do? Well, if medicine affects males and females differently, then we'll analyze male and female participants separately: we'll run a one-way ANOVA for just medicine on either group. This is what's meant by “simple effects” in our flowchart.
ANOVA with Simple Effects - Split File
How can we analyze 2 (or more) groups of cases separately? Well, SPSS has a terrific solution for this, known as SPLIT FILE. It requires that we first sort our cases so we'll do so as well.
sort cases by gender.
split file separate by gender.
Minor note: SPLIT FILE does not change your data in any way. It merely affects your output as we'll see in a minute. You can simply undo it by running
SPLIT FILE OFF.
but don't do so yet; we first want to run our one-way ANOVAs for inspecting our simple effects.
ANOVA with Simple Effects in SPSS
Since we switched on our SPLIT FILE, we can now just run one-way ANOVAs. We'll use

 .
The screenshots below guide you through the next steps.
.
The screenshots below guide you through the next steps.
This results in the syntax below. Let's run it.
UNIANOVA bdi BY medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PLOT=PROFILE(medicine) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
/PRINT ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=medicine.
ANOVA Output - Between Subjects Effects
First off, note that the output window now contains all ANOVA results for male participants and then a similar set of results for females. According to our flowchart we should now inspect the main effect.
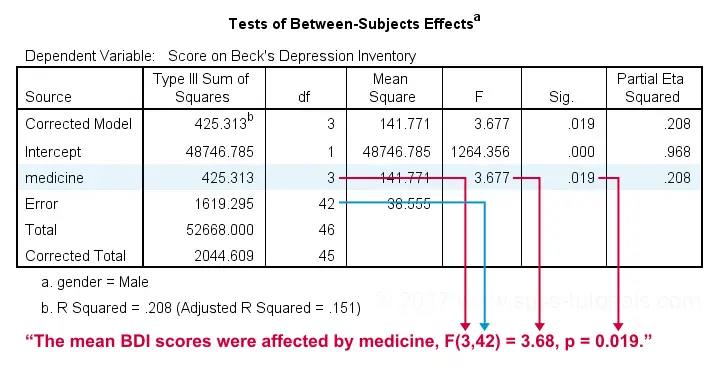
The effect for medicine is statistically significant. However, this just means it's probably not zero. But it's not very strong either as indicated by its partial eta squared of 0.208. This shouldn't come as a surprise. The 4 medicines don't differ much for males as we saw in our profile plots.
ANOVA Output - Post Hoc Tests
Our main effect suggests that our 4 medicines did not all perform similarly. But which one(s) really differ from which other one(s)? This question is addressed by our post hoc tests, in this case Tukey's HSD (“honestly significant differences”) comparisons.

This table compares each medicine with each other medicine (twice). The only comparison yielding p < 0.05 is “None” versus “Pharmaceutical”. Our profile plots show that these are the worst and best performing medicines for male participants. The means for all other medicines are too close to differ statistically significantly.
Female Participants
According to our flowchart, we're now done -at least for males. Interpreting the results for female participants is left as an exercise for the reader. However, I do want to point out the following:
- our profile plots show a much steeper line for females than for males.
- the main effect of medicine has a much higher partial eta squared of 0.63 for females.
- the effect of medicine has p = 0.000 for females and p = 0.019 for males.
- for females, all post hoc comparisons are statistically significant except for “Homeopathic” versus “Placebo” (p = 0.997).
All these findings indicate a much stronger effect of medicine for females than for males; there's a substantial interaction effect between medicine and gender on BDI scores. And this -again- is the reason why we need to analyze these groups separately and rerun our ANOVA with simple effects -like we just did.
Final Notes
Do you still think running a two-way ANOVA with an interaction effect is challenging? I hope this tutorial helped you understand the main line of thinking. And -hopefully!- things start to sink in for you -perhaps after a second reading.
SPSS ANOVA with Post Hoc Tests
Contents
- Descriptive Statistics for Subgroups
- ANOVA - Flowchart
- SPSS ANOVA Dialogs
- SPSS ANOVA Output
- SPSS ANOVA - Post Hoc Tests Output
- APA Style Reporting Post Hoc Tests
Post hoc tests in ANOVA test if the difference between
each possible pair of means is statistically significant.
This tutorial walks you through running and understanding post hoc tests using depression.sav, partly shown below.
The variables we'll use are
 the medicine that our participants were randomly assigned to and
the medicine that our participants were randomly assigned to and
 their levels of depressiveness measured 16 weeks after starting medication.
their levels of depressiveness measured 16 weeks after starting medication.
Our research question is whether some medicines result in lower depression scores than others. A better analysis here would have been ANCOVA but -sadly- no depression pretest was administered.
Quick Data Check
Before jumping blindly into any analyses, let's first see if our data look plausible in the first place. A good first step is inspecting a histogram which I'll run from the SPSS syntax below.
frequencies bdi
/format notable
/histogram.
Result
First off, our histogram (shown below) doesn't show anything surprising or alarming.
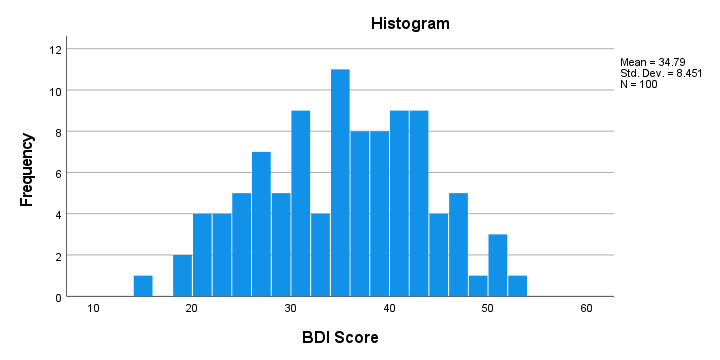
Also, note that N = 100 so this variable does not have any missing values. Finally, it could be argued that a single participant near 15 points could be an outlier. It doesn't look too bad so we'll just leave it for now.
Descriptive Statistics for Subgroups
Let's now run some descriptive statistics for each medicine group separately. The right way for doing so is from

 or simply typing the 2 lines of syntax shown below.
or simply typing the 2 lines of syntax shown below.
means bdi by medicine
/cells count min max mean median stddev skew kurt.
Result
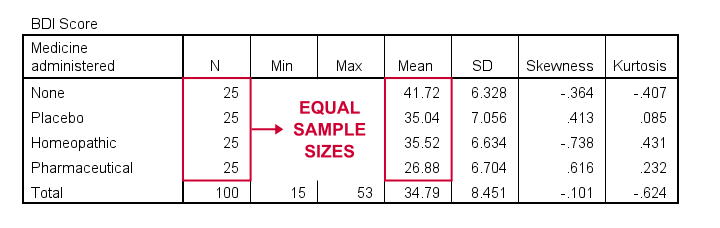
As shown, I like to present a nicely detailed table including the
for each group separately. But most important here are the sample sizes because these affect which assumptions we'll need for our ANOVA.
Also note that the mean depression scores are quite different across medicines. However, these are based on rather small samples. So the big question is: what can we conclude about the entire populations? That is: all people who'll take these medicines?
ANOVA - Null Hypothesis
In short, our ANOVA tries to demonstrate that some medicines work better than others by nullifying the opposite claim. This null hypothesis states that
the population mean depression scores are equal
across all medicines.
An ANOVA will tell us if this is credible, given the sample data we're analyzing. However, these data must meet a couple of assumptions in order to trust the ANOVA results.
ANOVA - Assumptions
ANOVA requires the following assumptions:
- independent observations;
- normality: the dependent variable must be normally distributed within each subpopulation we're comparing. However, normality is not needed if each n > 25 or so.
- homogeneity: the variance of the dependent variable must be equal across all subpopulations we're comparing. However, homogeneity is not needed if all sample sizes are roughly equal.
Now, homogeneity is only required for sharply unequal sample sizes. In this case, Levene's test can be used to examine if homogeneity is met. What to do if it isn't, is covered in SPSS ANOVA - Levene’s Test “Significant”.
ANOVA - Flowchart
The flowchart below summarizes when/how to check the ANOVA assumptions and what to do if they're violated.
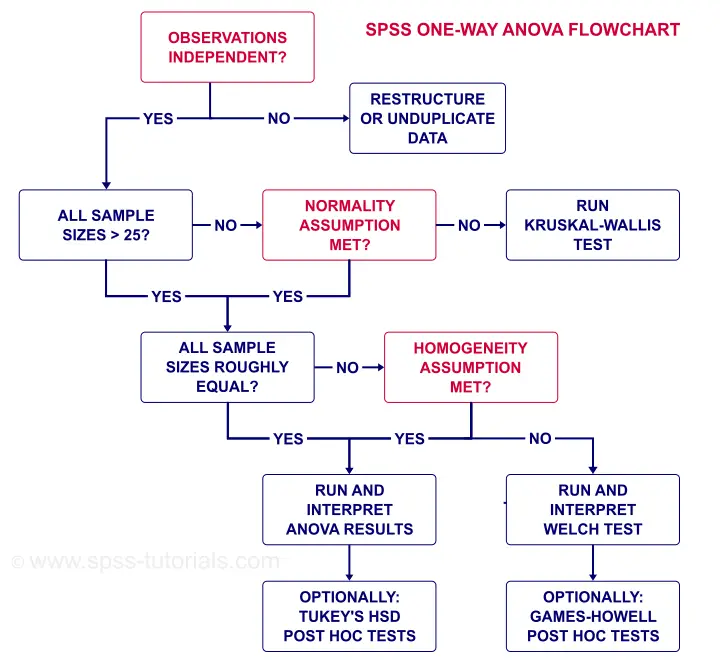
Note that depression.sav contains 4 medicine samples of n = 25 independent observations. It therefore meets all ANOVA assumptions.
SPSS ANOVA Dialogs
We'll run our ANOVA from

 as shown below.
as shown below.

Next, let's fill out the dialogs as shown below.
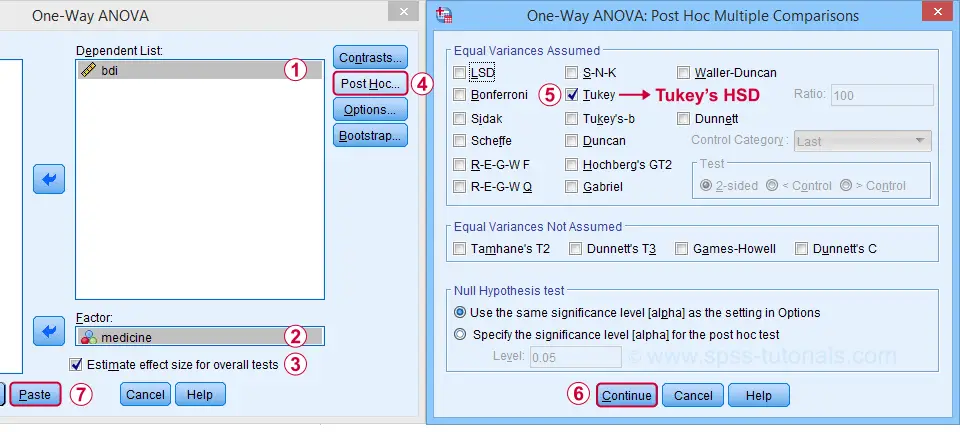
 Estimate effect size(...) is only available for SPSS version 27 or higher. If you're on an older version, you can get it from
Estimate effect size(...) is only available for SPSS version 27 or higher. If you're on an older version, you can get it from

 (“ANOVA table” under “Options”).
(“ANOVA table” under “Options”).
 Tukey's HSD (“honestly significant difference”) is the most common post hoc test for ANOVA. It is listed under “equal variances assumed”, which refers to the homogeneity assumption. However, this is not needed for our data because our sample sizes are all equal.
Tukey's HSD (“honestly significant difference”) is the most common post hoc test for ANOVA. It is listed under “equal variances assumed”, which refers to the homogeneity assumption. However, this is not needed for our data because our sample sizes are all equal.
Completing these steps results in the syntax below.
ONEWAY bdi BY medicine
/ES=OVERALL
/MISSING ANALYSIS
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY ALPHA(0.05).
SPSS ANOVA Output
First off, the ANOVA table shown below addresses the null hypothesis that all population means are equal. The significance level indicates that p < .001 so we reject this null hypothesis. The figure below illustrates how this result should be reported.
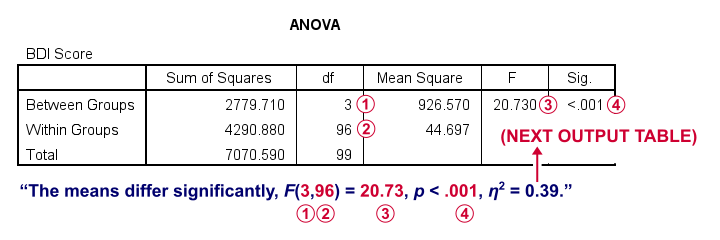
What's absent from this table, is eta squared, denoted as η2. In SPSS 27 and higher, we find this in the next output table shown below.
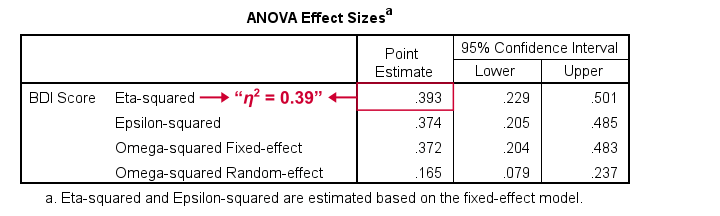
Eta-squared is an effect size measure: it is a single, standardized number that expresses how different several sample means are (that is, how far they lie apart). Generally accepted rules of thumb for eta-squared are that
- η2 = 0.01 indicates a small effect;
- η2 = 0.06 indicates a medium effect;
- η2 = 0.14 indicates a large effect.
For our example, η2 = 0.39 is a huge effect: our 4 medicines resulted in dramatically different mean depression scores.
This may seem to complete our analysis but there's one thing we don't know yet: precisely which mean differs from which mean? This final question is answered by our post hoc tests that we'll discuss next.
SPSS ANOVA - Post Hoc Tests Output
The table below shows if the difference between each pair of means is statistically significant. It also includes 95% confidence intervals for these differences.
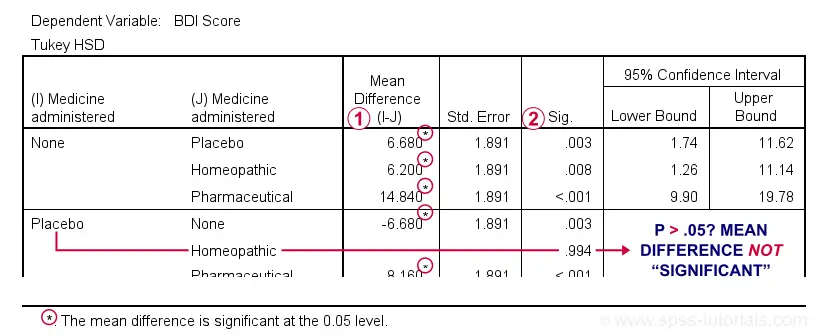
 Mean differences that are “significant” at our chosen α = .05 are flagged. Note that each mean differs from each other mean except for Placebo versus Homeopathic.
Mean differences that are “significant” at our chosen α = .05 are flagged. Note that each mean differs from each other mean except for Placebo versus Homeopathic.
 If we take a good look at the exact 2-tailed p-values, we see that they're all < .01 except for the aforementioned comparison.
If we take a good look at the exact 2-tailed p-values, we see that they're all < .01 except for the aforementioned comparison.
Given this last finding, I suggest rerunning our post hoc tests at α = .01 for reconfirming these findings. The syntax below does just that.
ONEWAY bdi BY medicine
/ES=OVERALL
/MISSING ANALYSIS
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY ALPHA(0.01).
APA Style Reporting Post Hoc Tests
The table below shows how to report post hoc tests in APA style.
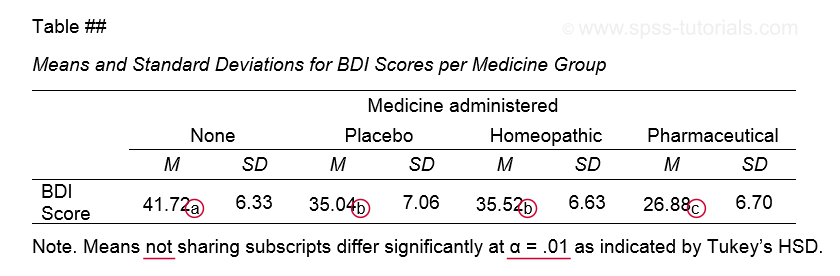
This table itself was created with a MEANS command like we used for Descriptive Statistics for Subgroups. The subscripts are based on the Homogeneous Subsets table in our ANOVA output.
Note that we chose α = .01 instead of the usual α = .05. This is simply more informative for our example analysis because all of our p-values < .05 are also < .01.
This APA table also seems available from

 but I don't recommend this: the p-values from Custom Tables seem to be based on Bonferroni adjusted independent samples t-tests instead of Tukey's HSD. The general opinion on this is that this procedure is overly conservative.
but I don't recommend this: the p-values from Custom Tables seem to be based on Bonferroni adjusted independent samples t-tests instead of Tukey's HSD. The general opinion on this is that this procedure is overly conservative.
Final Notes
Right, so a common routine for ANOVA with post hoc tests is
- run a basic ANOVA to see if the population means are all equal. This is often referred to as the omnibus test (omnibus is Latin, meaning something like “about all things”);
- only if we reject this overall null hypothesis, then find out precisely which pairs of means differ with post hoc tests (post hoc is Latin for “after that”).
Running post hoc tests when the omnibus test is not statistically significant is generally frowned upon. Some scenarios could perhaps justify doing so but let's leave that discussion for another day.
Right, so that should do. I hope you found this tutorial helpful. If you've any questions or remarks, please throw me a comment below. Other than that...
thanks for reading!
SPSS One-Way ANOVA Tutorial
For reading up on some basics, see ANOVA - What Is It?
- One-Way ANOVA - Null Hypothesis
- ANOVA Assumptions
- SPSS ANOVA Flowchart
- SPSS One-Way ANOVA Dialog
- SPSS ANOVA Output
- ANOVA - APA Reporting Guidelines
ANOVA Example - Effect of Fertilizers on Plants
A farmer wants to know which fertilizer is best for his parsley plants. So he tries different fertilizers on different plants and weighs these plants after 6 weeks. The data -partly shown below- are in parsley.sav.
Quick Data Check - Split Histograms
After opening our data in SPSS, let's first see what they basically look like. A quick way for doing so is inspecting a histogram of weights for each fertilizer separately. The screenshot below guides you through.
After following these steps, clicking results in the syntax below. Let's run it.
GRAPH
/HISTOGRAM=grams
/PANEL COLVAR=fertilizer COLOP=CROSS.
Result
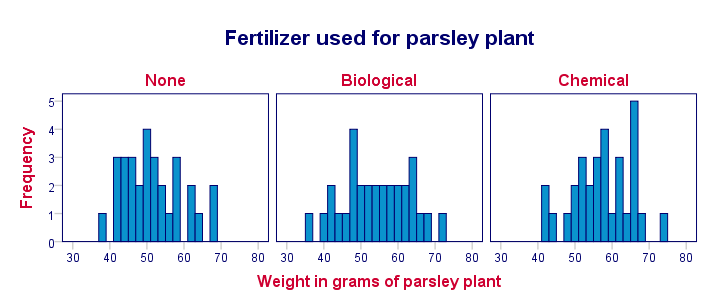
Importantly, these distributions look plausible and we don't see any outliers: our data seem correct to begin with -not always the case with real-world data!
Conclusion: the vast majority of weights are between some 40 and 65 grams and they seem reasonably normally distributed.
Inspecting Sample Sizes and Means
Precisely how did the fertilizers affect the plants? Let's compare some descriptive statistics for fertilizers separately. The quickest way is using MEANS which we could paste from

 but just typing the syntax may be just as easy.
but just typing the syntax may be just as easy.
means grams by fertilizer
/cells count mean stddev.
Result
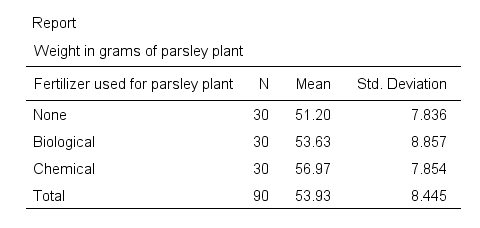
- We have sample sizes of n = 30 for each fertilizer.
- Second, the chemical fertilizer resulted in the highest mean weight of almost 57 grams. “None” performed worst at some 51 grams while “Biological” is in between.
- “Biological” has a slightly higher standard deviation than the other conditions but the difference is pretty small.
Now, this table tells us a lot about our samples of plants. But what do our sample means say about the population means? Can we say anything about the effects of fertilizers on all (future) plants? We'll try to do so by refuting the statement that all fertilizers perform equally: our null hypothesis.
One-Way ANOVA - Null Hypothesis
The null hypothesis for ANOVA is that
all population means are equal.
If this is true, then our sample means will probably differ a bit anyway. However, very different sample means contradict the hypothesis that the population means are equal. In this case, we may conclude that this null hypothesis probably wasn't true after all.
ANOVA will basically tells us to what extent our null hypothesis is credible. However, it requires some assumptions regarding our data.
ANOVA Assumptions
- independent observations: each record in the data must be a distinct and independent entity.Precisely, the assumption is “independent and identically distributed variables” but a thorough explanation is way beyond the scope of this tutorial.
- normality: the dependent variable is normally distributed in the population. Normality is not needed for reasonable sample sizes, say each n ≥ 25.
- homogeneity: the variance of the dependent variable must be equal in each subpopulation. Homogeneity is only needed for (sharply) unequal sample sizes. In this case, Levene's test can be used to see if homogeneity is met.
So how to check if we meet these assumptions? And what to do if we violate them? The simple flowchart below guides us through.
SPSS ANOVA Flowchart
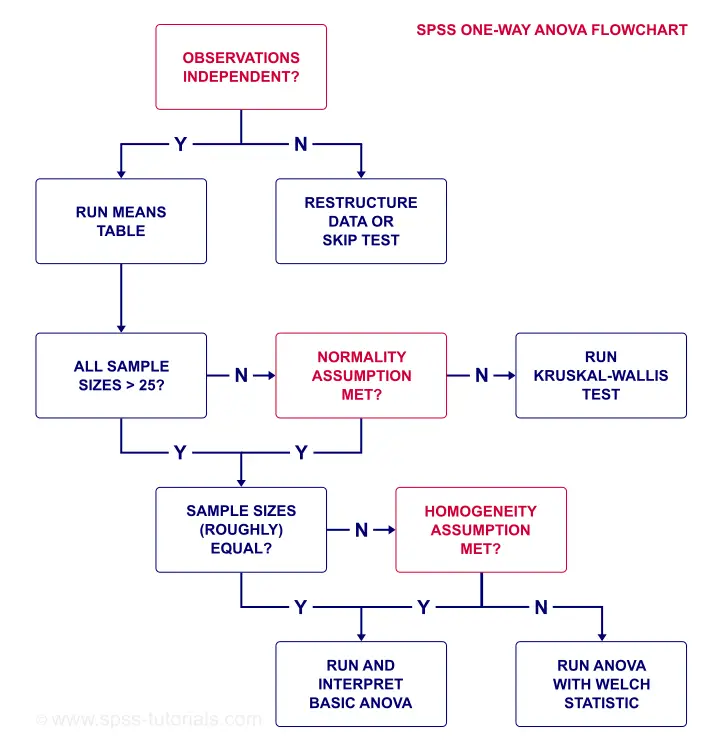
So what about our data?
- Our plants seem to be independent observations: each has a different id value (first variable).
- Our means table shows that each n ≥ 25 so we don't need to meet normality.
- Since our sample sizes are equal, we don't need the homogeneity assumption either.
So why do we inspect our sample sizes based on a means table? Why didn't we just look at the frequency distribution for fertilizer? Well, our ANOVA uses only cases without missing values on our dependent variable. And our means table shows precisely those.
A second reason is that we need to report the means and standard deviations per group. And the means table gives us precisely the statistics we want in the order we want them.
SPSS One-Way ANOVA Dialog
We'll now run a basic ANOVA from the menu. The screenshot below guides you through.
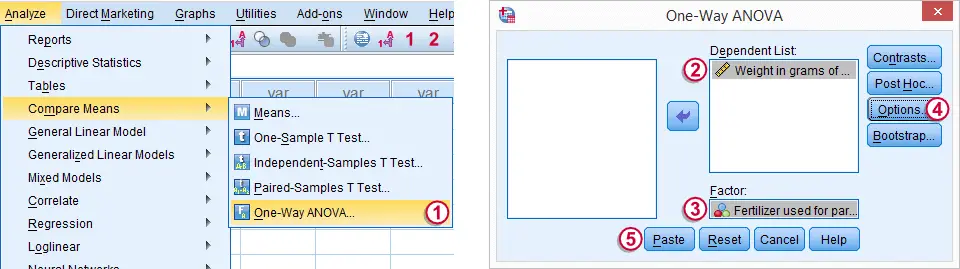
The button creates the syntax below.
One-Way ANOVA Syntax
ONEWAY grams BY fertilizer
/MISSING ANALYSIS.
SPSS One-Way ANOVA Output
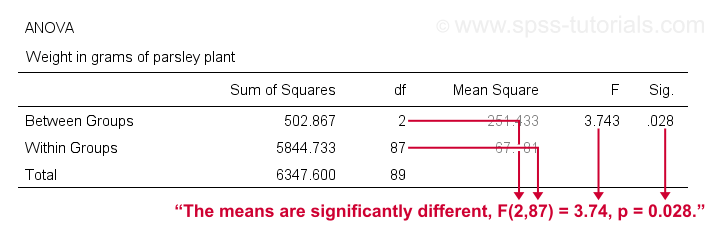
A general rule of thumb is that we
reject the null hypothesis if “Sig.” or p < 0.05
which is the case here. So we reject the null hypothesis that all population means are equal.
Conclusion: different fertilizers perform differently. The differences between our mean weights -ranging from 51 to 57 grams- are statistically significant.
ANOVA - APA Reporting Guidelines
First and foremost, we'll report our means table. Regarding the significance test, the APA suggests we report
- the F value;
- df1, the numerator degrees of freedom;
- df2, the denominator degrees of freedom;
- the p value
like so: “our three fertilizer conditions resulted in different mean weights for the parsley plants, F(2,87) = 3.7, p = .028.”
One-Way ANOVA - Next Steps
For this example, there's 2 more things we could take a look at:
- Post hoc tests: our ANOVA results tell us that not all population means are equal. But precisely which mean differs from which other mean? This is answered by running post hoc tests. For an outstanding tutorial, consult SPSS - One Way ANOVA with Post Hoc Tests Example.
- Effect size: we concluded that fertilizers affect mean weights but how strong is this effect? A common effect size measure for ANOVA is partial eta squared. Sadly, effect size is absent from the One-Way dialog.
Oddly, MEANS does include eta-squared but lacks other essential options such as Levene’s test. For complete output, you need to run your ANOVA twice from 2 different commands. This really is a major stupidity in SPSS. There. I said it.
ANOVA with Eta-Squared from MEANS
means grams by fertilizer
/statistics anova.
Result

Right, so that's about the most basic SPSS ANOVA tutorial I could come up with. I hope you found it helpful. Let me know what you think by throwing me a comment below.
Thanks for reading!
How to Run Levene’s Test in SPSS?
Levene’s test examines if 2+ populations all have
equal variances on some variable.
Levene’s Test - What Is It?
If we want to compare 2(+) groups on a quantitative variable, we usually want to know if they have equal mean scores. For finding out if that's the case, we often use
- an independent samples t-test for comparing 2 groups or
- a one-way ANOVA for comparing 3+ groups.
Both tests require the homogeneity (of variances) assumption: the population variances of the dependent variable must be equal within all groups. However, you don't always need this assumption:
- you don't need to meet the homogeneity assumption if the groups you're comparing have roughly equal sample sizes;
- you do need this assumption if your groups have sharply different sample sizes.
Now, we usually don't know our population variances but we do know our sample variances. And if these don't differ too much, then the population variances being equal seems credible.
But how do we know if our sample variances differ “too much”? Well, Levene’s test tells us precisely that.
Null Hypothesis
The null hypothesis for Levene’s test is that the groups we're comparing all have equal population variances. If this is true, we'll probably find slightly different variances in samples from these populations. However, very different sample variances suggest that the population variances weren't equal after all. In this case we'll reject the null hypothesis of equal population variances.
Levene’s Test - Assumptions
Levene’s test basically requires two assumptions:
- independent observations and
- the test variable is quantitative -that is, not nominal or ordinal.
Levene’s Test - Example
A fitness company wants to know if 2 supplements for stimulating body fat loss actually work. They test 2 supplements (a cortisol blocker and a thyroid booster) on 20 people each. An additional 40 people receive a placebo.
All 80 participants have body fat measurements at the start of the experiment (week 11) and weeks 14, 17 and 20. This results in fatloss-unequal.sav, part of which is shown below.
One approach to these data is comparing body fat percentages over the 3 groups (placebo, thyroid, cortisol) for each week separately.Perhaps a better approach to these data is using a single mixed ANOVA. Weeks would be the within-subjects factor and supplement would be the between-subjects factor. For now, we'll leave it as an exercise to the reader to carry this out. This can be done with an ANOVA for each of the 4 body fat measurements. However, since we've unequal sample sizes, we first need to make sure that our supplement groups have equal variances.
Running Levene’s test in SPSS
Several SPSS commands contain an option for running Levene’s test. The easiest way to go -especially for multiple variables- is the One-Way ANOVA dialog.This dialog was greatly improved in SPSS version 27 and now includes measures of effect size such as (partial) eta squared. So let's navigate to and fill out the dialog that pops up.
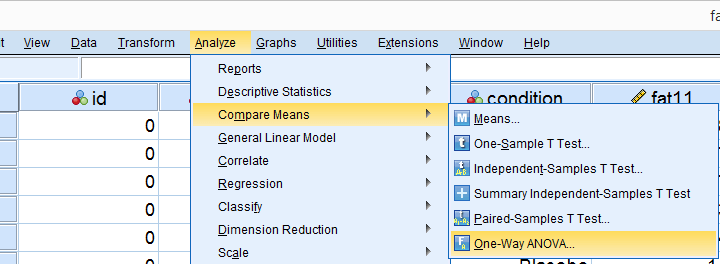
As shown below,  the Homogeneity of variance test under Options refers to Levene’s test.
the Homogeneity of variance test under Options refers to Levene’s test.
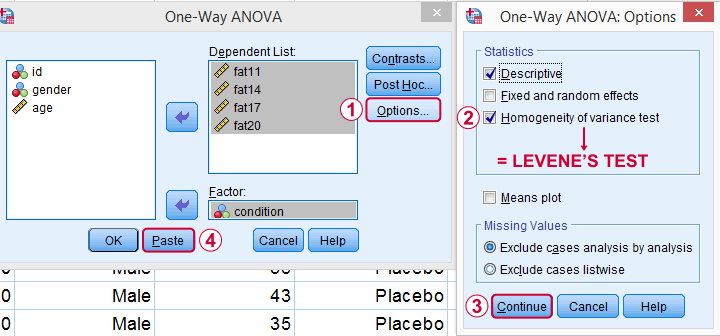
Clicking results in the syntax below. Let's run it.
SPSS Levene’s Test Syntax Example
ONEWAY fat11 fat14 fat17 fat20 BY condition
/STATISTICS DESCRIPTIVES HOMOGENEITY
/MISSING ANALYSIS.
Output for Levene’s test
On running our syntax, we get several tables. The second -shown below- is the Test of Homogeneity of Variances. This holds the results of Levene’s test.
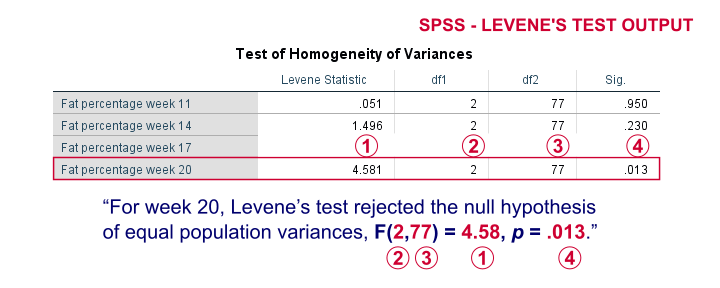
As a rule of thumb, we conclude that population variances are not equal if “Sig.” or p < .05. For the first 2 variables, p > .05: for fat percentage in weeks 11 and 14 we don't reject the null hypothesis of equal population variances.
For the last 2 variables, p < .05: for fat percentages in weeks 17 and 20, we reject the null hypothesis of equal population variances. So these 2 variables violate the homogeneity of variance assumption needed for an ANOVA.
Descriptive Statistics Output
Remember that we don't need equal population variances if we have roughly equal sample sizes. A sound way for evaluating if this holds is inspecting the Descriptives table in our output.
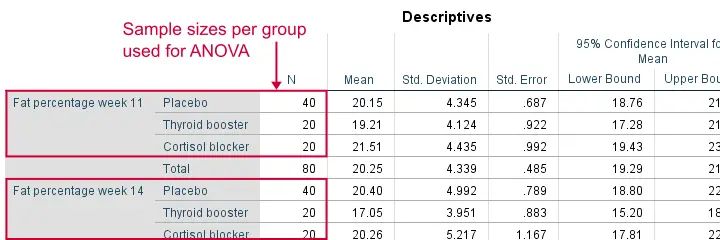
As we see, our ANOVA is based on sample sizes of 40, 20 and 20 for all 4 dependent variables. Because they're not (roughly) equal, we do need the homogeneity of variance assumption but it's not met by 2 variables.
In this case, we'll report alternative measures (Welch and Games-Howell) that don't require the homogeneity assumption. How to run and interpret these is covered in SPSS ANOVA - Levene’s Test “Significant”.
Reporting Levene’s test
Perhaps surprisingly, Levene’s test is technically an ANOVA as we'll explain here. We therefore report it like just a basic ANOVA too. So we'll write something like “Levene’s test showed that the variances for body fat percentage in week 20 were not equal, F(2,77) = 4.58, p = .013.”
Levene’s Test - How Does It Work?
Levene’s test works very simply: a larger variance means that -on average- the data values are “further away” from their mean. The figure below illustrates this: watch the histograms become “wider” as the variances increase.
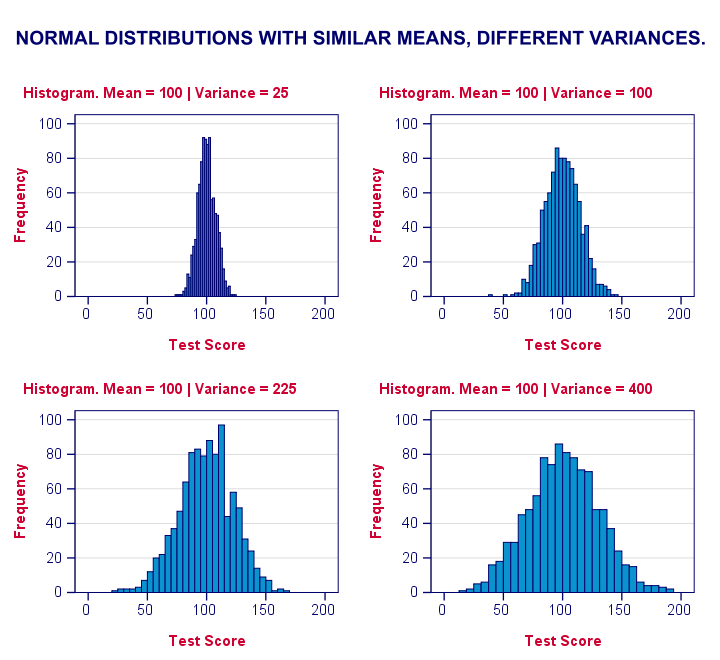
We therefore compute the absolute differences between all scores and their (group) means. The means of these absolute differences should be roughly equal over groups. So technically, Levene’s test is an ANOVA on the absolute difference scores. In other words: we run an ANOVA (on absolute differences) to find out if we can run an ANOVA (on our actual data).
If that confuses you, try running the syntax below. It does exactly what I just explained.
“Manual” Levene’s Test Syntax
aggregate outfile * mode addvariables
/break condition
/mfat20 = mean(fat20).
*Compute absolute differences between fat20 and group means.
compute adfat20 = abs(fat20 - mfat20).
*Run minimal ANOVA on absolute differences. F-test identical to previous Levene's test.
ONEWAY adfat20 BY condition.
Result
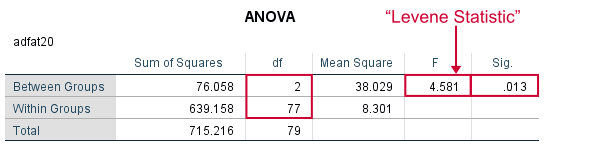
As we see, these ANOVA results are identical to Levene’s test in the previous output. I hope this clarifies why we report it as an ANOVA as well.
Thanks for reading!
SPSS RM ANOVA – 2 Within-Subjects Factors
- Repeated Measures ANOVA - Null Hypothesis
- Repeated Measures ANOVA - Assumptions
- Factorial ANOVA - Basic Flowchart
- Factorial Repeated Measures ANOVA in SPSS
- Repeated Measures ANOVA - APA Style Reporting
How does alcohol consumption affect driving performance? A study tested 36 participants during 3 conditions:
- no alcohol - 0 glasses of beer;
- medium alcohol - 2 glasses of beer;
- high alcohol - 4 glasses of beer.
Each participant went through all 3 conditions in random order on 3 consecutive days. During each condition, the participants drove for 30 minutes in a driving simulator. During these “rides” they were confronted with 5 trials: dangerous situations to which they need to respond fast. The 15 reaction times (5 trials for each of 3 conditions) are in alcoholtest.sav, part of which is shown below.
The main research questions are
- how does alcohol affect reaction times?
- how does trial affect reaction times?
- does the effect of alcohol depend on trial?
We'll obviously inspect the mean reaction times over (combinations of) conditions and trials. However, we've only 36 participants. Based on this tiny sample, what -if anything- can we conclude about the general population? The right way to answer that is running a repeated measures ANOVA over our 15 reaction time variables.
Repeated Measures ANOVA - Null Hypothesis
Generally, the null hypothesis for a repeated measures ANOVA is that
the population means of 3+ variables are all equal.
If this is true, then the corresponding sample means may differ somewhat. However, very different sample means are unlikely if population means are equal. So if that happens, we no longer believe that the population means were truly equal: we reject this null hypothesis.
Now, with 2 factors -condition and trial- our means may be affected by condition, trial or the combination of condition and trial: an interaction effect. We'll examine each of these possible effect separately. This means we'll test 3 null hypotheses:
- population means are equal over conditions;
- population means are equal over trials;
- population means are equal over combinations of condition and trial.
As we're about to see: we may or may not reject each of our 3 hypotheses independently of the others.
Repeated Measures ANOVA - Assumptions
A repeated measures ANOVA will usually run just fine in SPSS. However, we can only trust the results if we meet some assumptions. These are:
- Independent observations or -precisely- independent and identically distributed variables.
- Normality: the test variables follow a multivariate normal distribution in the population. This is only needed for small sample sizes of N < 25 or so. You can test if variables are normally distributed with a Kolmogorov-Smirnov test or a Shapiro-Wilk test.
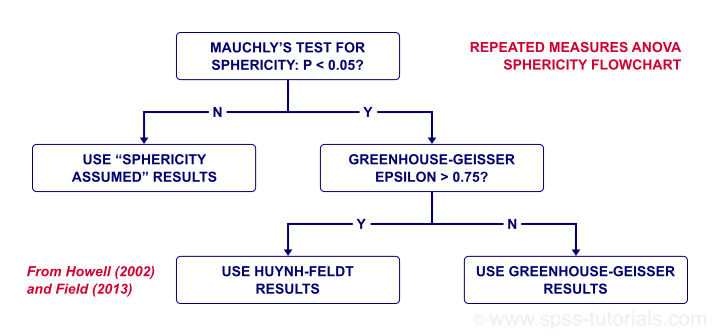
- Sphericity: the population variances of all difference scores among the test variables must be equal. Sphericity is often tested with Mauchly’s test.
With regard to our example data in alcoholtest.sav:
- Independent observations is probably met: each case contains a separate person who didn't interact in any way with any other participants.
- We don't need normality because we've a reasonable sample size of N = 36.
- We'll use Mauchly's test to see if sphericity is met. If it isn't, we'll apply a correction to our results as shown in our sphericity flowchart.
Data Checks I - Histograms
Let's first see if our data look plausible in the first place. Since our 15 reaction times are quantitative variables, running some basic histograms over them will give us some quick insights. The fastest way to do so is running the syntax below. Easier -but slower- alternatives are covered in Creating Histograms in SPSS.
frequencies no_1 to hi_5
/format notable
/histogram.
I won't bother you with the output. See for yourself that all frequency distributions look at least reasonably plausible.
Data Checks II - Missing Values
In SPSS, repeated measures ANOVA uses
only cases without any missing values
on any of the test variables. That's right: cases having one or more missing values on the 15 reaction times are completely excluded from the analysis. This is a major pitfall and it's hard to detect after running the analysis.
Our advice is to
inspect how many cases are complete on all test variables
before running the actual analysis. A very fast way to do so is running a minimal DESCRIPTIVES table.
descriptives no_1 to hi_5.
Result
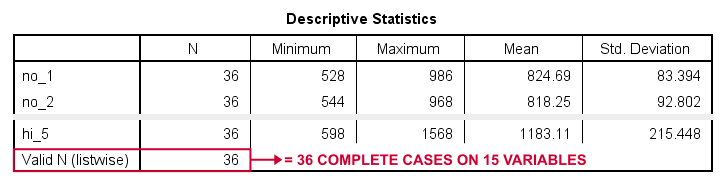
“Valid N (listwise)” indicates the number of cases who are complete on all variables in this table. For our example data, all 36 cases are complete. All cases will be used for our repeated measures ANOVA.
If missing values do occur in other data, you may want to exclude such cases altogether before proceeding. The simplest options are FILTER or SELECT IF. Alternatively, you could try and impute some -or all- missing values.
Creating a Reporting Table
Our last step before the actual ANOVA is creating a table with descriptive statistics for reporting. The APA suggests using 1 row per variable that includes something like
- sample size;
- mean;
- 95% confidence interval for the mean;
- median;
- standard deviation and
- skewness.
A minimal EXAMINE table comes close:
examine no_1 to hi_5.
Sadly, there's some issues with EXAMINE that you must know:
- by default, EXAMINE uses only cases that are complete on all variables in the table. We usually don't want that. However, for this example it's great because our final ANOVA is also restricted to complete cases.
- EXAMINE only reports sample sizes in a separate table. This is utter stupidity. However, for this example it's ok: we know we've 36 complete cases. We'll report this in the table title.
- EXAMINE creates way more output than you need and you can't choose which statistics you'll get in which order. The least cumbersome solution is editing the table in Excel.
After creating the table, we'll rearrange its dimensions like we did in SPSS Correlations in APA Format. The result is shown below.
Reporting Table - Result
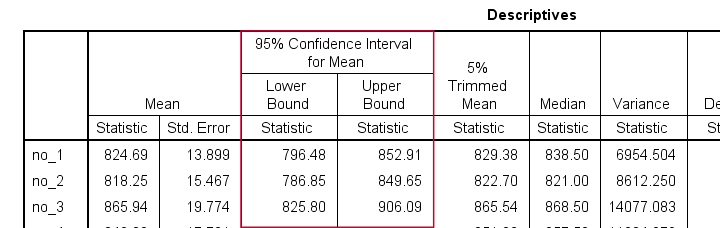
This table contains all descriptives we'd like to report. Moreover, it also allows us to double-check some of the later ANOVA output.
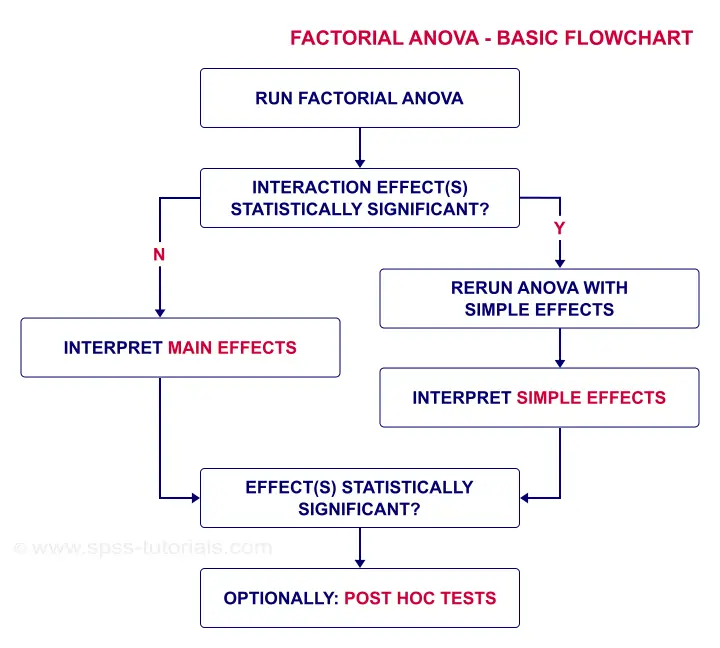
Factorial ANOVA - Basic Flowchart
Factorial Repeated Measures ANOVA in SPSS
The screenshots below guide you through running the actual ANOVA. Note that you'll only have in your menu if you're licensed for the Advanced Statistics module.
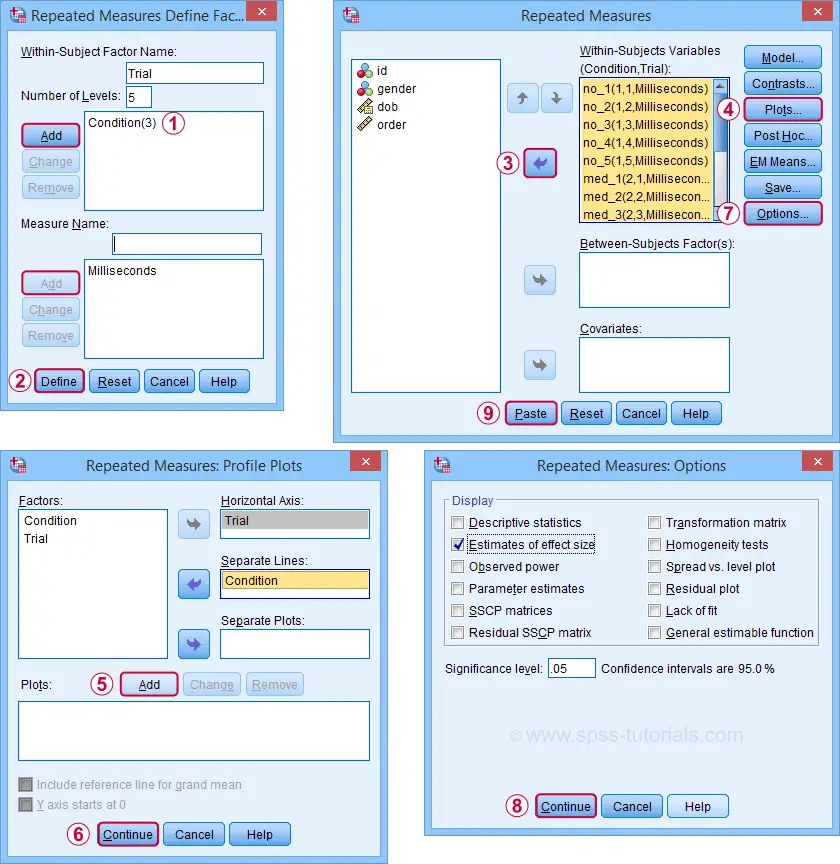
Completing these steps results in the syntax below. Let's run it.
GLM no_1 med_1 hi_1
/WSFACTOR=Condition_1 3 Polynomial
/MEASURE=Milliseconds
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(Condition_1) COMPARE ADJ(BONFERRONI)
/PRINT=ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=Condition_1.
ANOVA Results I - Mauchly's Test
As indicated by our flowchart, we first inspect the interaction effect: condition by trial. Before looking up its significance level, let's first see if sphericity holds for this effect. We find this in the “Mauchly's Test of Sphericity” table shown below.
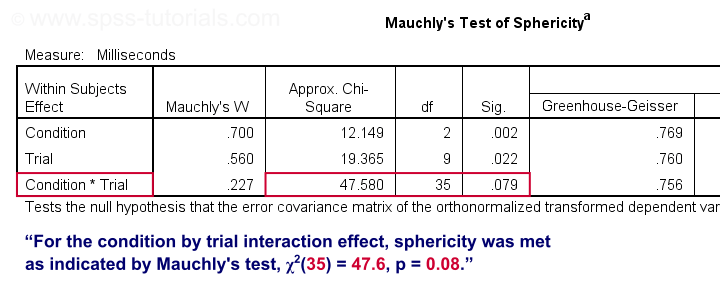
As a rule of thumb, we reject the null hypothesis if p < 0.05. For the interaction effect, “Sig.” or p = 0.079. We retain the null hypothesis. For Mauchly's test, the null hypothesis is that sphericity holds. Conclusion: the sphericity assumption seems to be met. Let's now see if the interaction effect is statistically significant.
ANOVA Results II - Within-Subjects Effects
In the Tests of Within-Subjects Effects table, each effect has 4 rows. We just saw that sphericity holds for the condition by trial interaction. We therefore only use the rows labeled “Sphericity Assumed” as shown below.
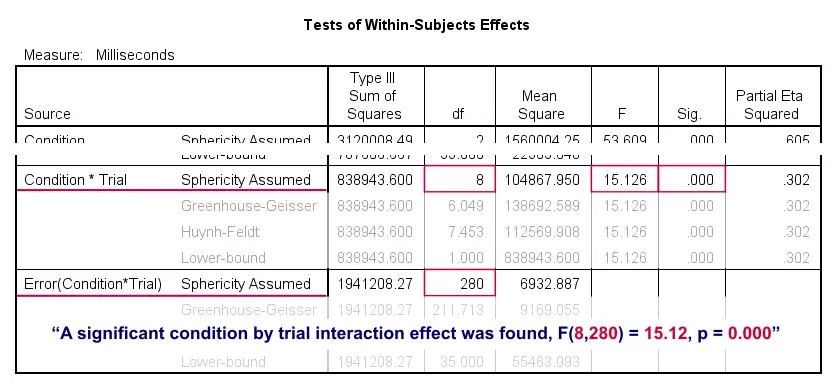
First off, “Sig.” or p = 0.000: the interaction effect is extremely statistically significant. Also note that its effect size -partial eta squared- is 0.302. This indicates a strong effect for condition by trial. But what does that mean? The best way to find out is inspecting our profile plot.
ANOVA Results III - Profile Plot
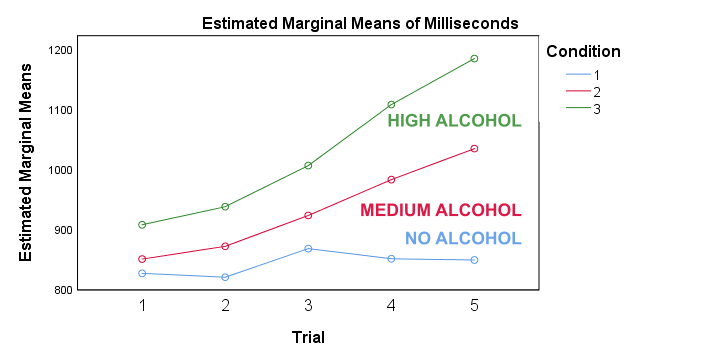
First off, the “estimated marginal means” are simply the observed sample means when running the full factorial model -the default in SPSS. If you're not sure, you can verify this from the reporting table we created earlier. Anyway, what we see is that
- reaction times don't clearly increase over trials for the no alcohol condition;
- reaction times somewhat increase over trials after medium alcohol consumption and
- reaction times strongly increase in the high alcohol condition.
In short, the interaction effect means that the effect of alcohol depends on trial. For the first trial, the lines -representing alcohol conditions- lie close together. But over trials, they diverge further and further. The largest effect of alcohol is seen for trial 5: the reaction times run from 850 milliseconds (no alcohol) up to some 1,200 milliseconds (high alcohol). This implies that there's no such thing as the effect of alcohol. It depends on which trial we inspect. So the logical thing to do is analyze the effect of alcohol for each trial separately. Precisely this is meant by the simple effects suggested in our flowchart.
Rerunning the ANOVA with Simple Effects
So how to run simple effects? It really is simple: we run a one-way repeated measures ANOVA over the 3 conditions for trial 1 only. We'll then just repeat that for trials 2 through 5.
We'll include post hoc tests too. Surprisingly, the dialog is only for between-subjects factors -which we don't have now. For within-subjects factors, use the dialog as shown below.
Completing these steps results in the syntax below.
GLM no_5 med_5 hi_5
/WSFACTOR=Condition_5 3 Polynomial
/MEASURE=Milliseconds
/METHOD=SSTYPE(3)
/EMMEANS=TABLES(Condition_5) COMPARE ADJ(BONFERRONI)
/PRINT=ETASQ
/CRITERIA=ALPHA(.05)
/WSDESIGN=Condition_5.
Simple Effects Output I - Mauchly's Test

When comparing the 3 alcohol conditions for trial 1 only, Mauchly's test suggests that the sphericity assumption is violated. In this case, we report either
- the Greenhouse-Geisser corrected results or
- the Huyn-Feldt corrected results.
Precisely which depends on the Greenhouse-Geisser epsilon. Epsilon is the Greek letter e written as ε. It estimates to which extent sphericity holds. For this example, ε = 0.840 -a modest violation of sphericity. If ε > 0.75, we report the Huyn-Feldt corrected results as shown below.
Repeated Measures ANOVA - Sphericity Flowchart
Simple Effects Output II - Within-Subjects Effects
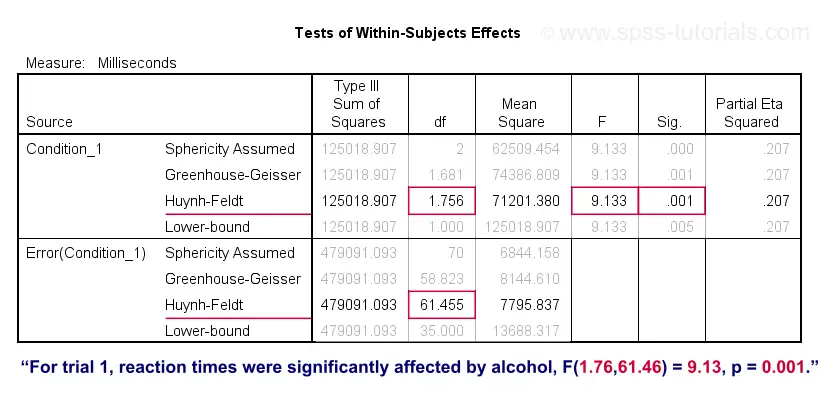
For trial 1, the 3 mean reaction times are significantly different because “Sig.” or p < 0.05. However, note that the effect size -partial eta squared- is modest: η2 = 0.207.
In any case, we conclude that the 3 means are not all equal. However, we don't know precisely which means are (not) different. As suggested by our flowchart, we can find out from the post hoc tests we ran.
Simple Effects Output III - Post Hoc Tests
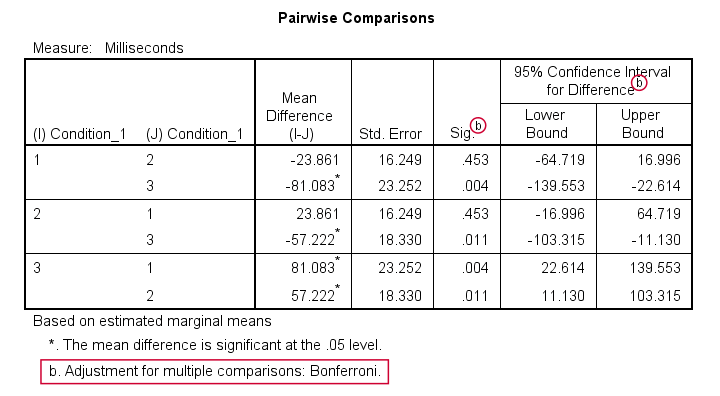
Precisely which means are (not) different? The Pairwise Comparisons table tells us that
only the mean difference between conditions 1 and 2
is not statistically significant.
So how do these tests work? What SPSS does here, is simply running a paired samples t-test between each pair of variables. For 3 conditions, this results in 3 such tests. Now, 3 tests have a bigger chance of coming up with a false result than 1 test. In order to correct for this, all p-values are multiplied by 3. This is the Bonferroni correction mentioned in the table comment. You can easily verify this by running
T-TEST PAIRS=no_1 med_1 hi_1.
This results in uncorrected p-values which are equal to the corrected p-values divided by 3.
So that'll do for trial 1. Analyzing trials 2-5 is left as an exercise to the reader.
Repeated Measures ANOVA - APA Style Reporting
First and foremost, present a table with descriptive statistics like the reporting table we created earlier.
Second, report the outcome of Mauchly's test for each effect you discuss:
“for trial 1, Mauchly's test indicated a violation
of the sphericity assumption, χ2(2) = 7.17, p = 0.028.”
If sphericity is violated, report the Greenhouse-Geisser ε and which corrected results you'll report:
“Since sphericity is violated (ε = 0.840),
Huyn-Feldt corrected results are reported.”
Finally, report the (corrected) F-test results for the within-subjects effects:
“Mean reaction times were affected by alcohol,
F(1.76,61.46) = 9.13, p = 0.001, η2 = 0.21.”
Note that η2 refers to (partial) eta squared, an effect size measure for ANOVA.
Thanks for reading.
SPSS Two-Way ANOVA – Quick Tutorial
Research Question
How to lose weight effectively? Do diets really work and what about exercise? In order to find out, 180 participants were assigned to one of 3 diets and one of 3 exercise levels. After two months, participants were asked how many kilos they had lost. These data -partly shown above- are in weightloss.sav.
We're going to test if the means for weight loss after two months are the same for diet, exercise level and each combination of a diet with an exercise level. That is, we'll compare more than two means so we end up with some kind of ANOVA.
Case Count and Histogram
We always want to have a basic idea what our data look like before jumping into any analyses. We first want to confirm that we really do have 180 cases. Next, we'd like to inspect the frequency distribution for weight loss with a histogram. We'll do so by running the syntax below.
show n.
*Inspect histogram for weight loss.
frequencies wloss
/format notable /*= don't create table because it's too large.
/histogram.
Result
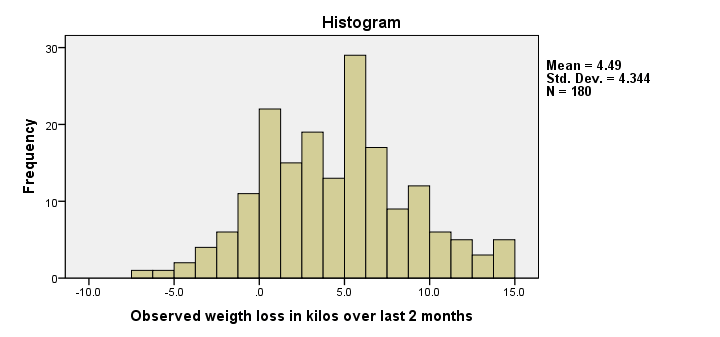
We have 180 cases indeed. Importantly, the histogram of weight loss looks plausible. We don't see any very high or low values that we should set as user missing values. One or two participants gained some 7 kilos (weight loss = -7) and some managed to lose up to 15 kilos. Furthermore, weight loss looks reasonably normally distributed.
Contingency Table Diet by Exercise
We now like to know how participants are distributed over diet and exercise. For our ANOVA, later on, we need to know if our design is balanced: are the percentages of participants in each diet equal over exercise levels? Some of you may notice that this question is actually the null hypothesis in a chi-square test. And that's exactly what we'll run next.
crosstabs diet by exercise
/statistics chisq.
Result

Note that each cell (combination of diet and exercise level) holds 20 participants. Note that our chi-square value is 0 (not shown in screenshot). This implies that we're dealing with a balanced design, which is a good thing because unbalanced designs somewhat complicate a two-way ANOVA.
Means Table
So did the diet and exercise have any effect? A very simple way for getting an idea of this is running a basic MEANS table.
means wloss by diet by exercise.
Result
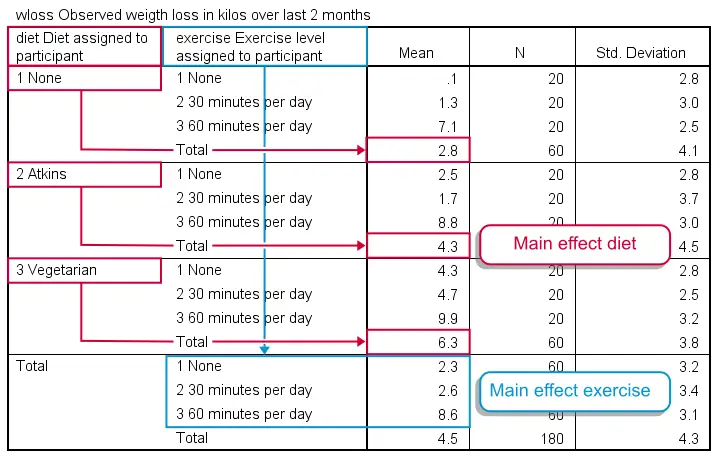
It may take a minute to see the pattern in this table but I did my best to highlight it with colors. Note that participants without any diet -all exercise levels taken together- lost an average of 2.8 kilos. The Atkins and vegetarian diets resulted in 6.3 and 4.3 kilos of weight loss on average. This is the main effect for diet: the differences in weight loss attributable to diet while taking together all exercise levels. In a similar vein, we see a somewhat stronger main effect for exercise with means running from 2.3 up to 8.6 kilos.
An interesting question is whether the effect of exercise depends on the diet followed. This is what we call an interaction effect. We'll explain it in a minute by visualizing our means in a chart.
Two Way ANOVA - Basic Idea
We just saw that different diets and exercise levels show different mean weight losses. However, we're looking at just a tiny sample. The situation in the (much larger) population may be different. Is it credible that we find these differences if neither diet nor exercise has any effect whatsoever in our population? We'll answer this question by running a two way ANOVA.
ANOVA Assumptions
In short, the main statistical assumptions required for ANOVA are
- independent observations: this often means that each case (row of data values) must represent a separate person (or other “object”). It's not allowed for a single person to appear as more than one case, which holds for our data.
- homoscedasticity: the standard deviation of our dependent variable (weight loss) must be equal for each (diet/exercise) group of respondents. Our previous means table shows that they are pretty similar indeed. Nevertheless, we'll also test this assumption more formally with Levene's test which is included in SPSS ANOVA procedure.
- a normally distributed dependent variable in the population. Our previous histogram suggests this holds for our data. On top of that, the normality assumption is of minor importance for larger sample sizes due to the central limit theorem.
SPSS Two Way ANOVA Menu
We choose whenever we analyze just one dependent variable (weight loss), regardless how many independent variables (diet and exercise) we may have.
Before pasting the syntax, we'll quickly jump into the subdialogs  ,
,  and
and  for adjusting some settings.
for adjusting some settings.
 Estimates of effect size will add partial eta squared in our output.
Estimates of effect size will add partial eta squared in our output.
 Homogeneity tests refers to Levene’s test. It assesses whether the population variances of our dependent variable are equal over the levels of our factors. This assumption is required for ANOVA.
Homogeneity tests refers to Levene’s test. It assesses whether the population variances of our dependent variable are equal over the levels of our factors. This assumption is required for ANOVA.
Profile plots visualize means for each combination of factors. As we'll see in a minute, this gives a lot of insight into how our factors relate to our dependent variable and -possibly- interact while doing so.
A basic ANOVA only tests the null hypothesis that all means are equal. If this is unlikely, then we'll usually want to know exactly which means are not equal. The most common post hoc test for finding out is Tukey’s HSD (short for Honestly Significant Difference).
SPSS Two Way ANOVA Syntax
Following through all steps results in the syntax below. We'll run it and discuss the results.
UNIANOVA wloss BY diet exercise
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=diet exercise (TUKEY)
/PLOT=PROFILE(exercise*diet)
/PRINT=ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=diet exercise diet*exercise.
Two Way ANOVA Output - Levene’s Test

Levene’s test does not reject the assumption of equal variances that's needed for our ANOVA results later on. We're good to go. Let's scroll down to the end of our output now for our profile plots first.
Two Way ANOVA Output - Profile Plots
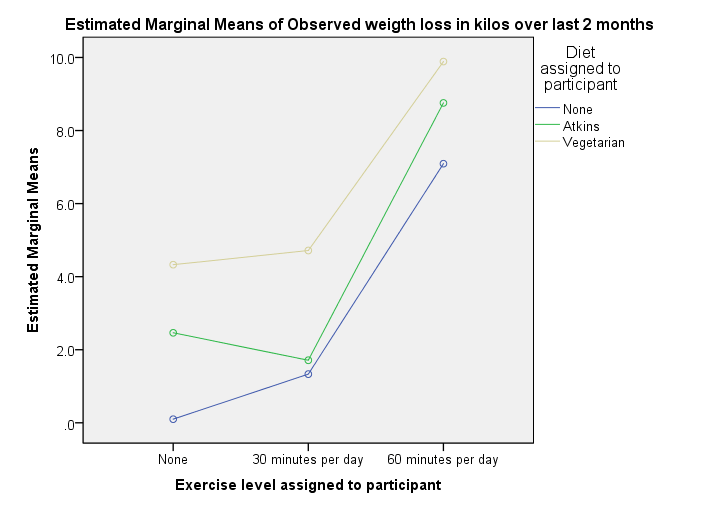
This basically says it all. We see each line rise steeply between 30 to 60 minutes of exercise per day. Second, a vegetarian diet always resulted in more weight loss than the other diets. Both diet and exercise seem to have a main effect on weight loss.
So what about our interaction effect? Well, the effect of exercise is visualized as a line for each diet group separately. Since these lines look pretty similar, our plot doesn't show much of an interaction effect. However, we'll try to confirm this with a more formal test in a minute.
Technical note: the “estimated marginal means” are equal to the observed means in our previous means table because we tested the saturated model (consisting of all main and interaction effects as this is the default setting in UNIANOVA).
Two Way ANOVA Output - Between Subjects Effects
Our means plot was very useful for describing the pattern of means resulting from diet and exercise in our sample. But perhaps things are different in the larger population. If neither diet nor exercise affect weight loss, could we find these sample results by mere sampling fluctuation? Short answer: no.
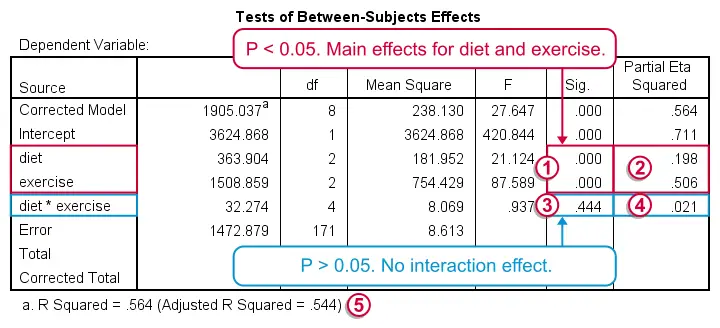
In Tests of Between-Subjects Effects, we're interested in 3 rows: our 2 main effects (diet and exercise) and 1 interaction effect (diet * exercise). We usually ignore the other rows such as “Corrected Model” and “Intercept”.
 First the interaction: if the effect of exercise is the same for all diets, then there's a 0.44 probability (p-value under “Sig” for “significance”) of finding our sample results. We usually report our df (“degrees of freedom”), F-value and p-value for each of our 3 effects separately:
“An interaction between diet and exercise could not be demonstrated, F(4,171) = .94, p = 0.44.”
First the interaction: if the effect of exercise is the same for all diets, then there's a 0.44 probability (p-value under “Sig” for “significance”) of finding our sample results. We usually report our df (“degrees of freedom”), F-value and p-value for each of our 3 effects separately:
“An interaction between diet and exercise could not be demonstrated, F(4,171) = .94, p = 0.44.”
 Further note that partial eta squared is only 0.021 for our interaction effect. This is basically negligible.
Further note that partial eta squared is only 0.021 for our interaction effect. This is basically negligible.
 If and only if there's no interaction effect, we'll look into the main effects, both of which have p = 0.000: if there's no main effects in our larger population, the probability of finding these sample main effects is basically zero.
If and only if there's no interaction effect, we'll look into the main effects, both of which have p = 0.000: if there's no main effects in our larger population, the probability of finding these sample main effects is basically zero.
 Partial eta squared is 0.51 for exercise and 0.20 for diet. That is, the relative impact of exercise is more than twice as strong as diet.
Partial eta squared is 0.51 for exercise and 0.20 for diet. That is, the relative impact of exercise is more than twice as strong as diet.
 Last but not least, adjusted r squared tells us that 54.4% of the variance in weight loss is attributable to diet and exercise. In social sciences research, this is a high value, indicating strong relationships between our factors and weight loss.
Last but not least, adjusted r squared tells us that 54.4% of the variance in weight loss is attributable to diet and exercise. In social sciences research, this is a high value, indicating strong relationships between our factors and weight loss.
Two Way ANOVA Output - Multiple Comparisons
We now know that the average weight loss is not equal for all different diets and exercise levels. So precisely which means are different? We can figure that out with post hoc tests, the most common of which is Tukey’s HSD, the output of which is shown below.
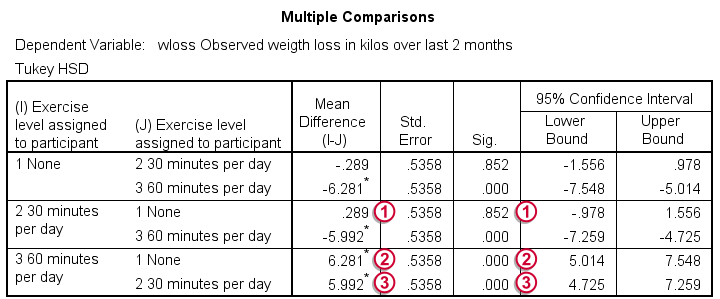
For 3 means, 3 comparisons are made (a-b, b-c and a-c). Each is reported twice in this table, resulting in 6 rows.
 The difference in weight loss between no exercise and 30 minutes is 0.29 kilos. If it is zero in our larger populations, there's an 85.2% probability of finding this in our sample. Our results don't demonstrate any effect of 30 minutes of exercise as compared to no exercise.
The difference in weight loss between no exercise and 30 minutes is 0.29 kilos. If it is zero in our larger populations, there's an 85.2% probability of finding this in our sample. Our results don't demonstrate any effect of 30 minutes of exercise as compared to no exercise.
 The difference between no exercise and 60 minutes is a whopping 6.28 kilos. Both the asterisk (*), confidence interval and p-value show that the difference is statistically significant.
The difference between no exercise and 60 minutes is a whopping 6.28 kilos. Both the asterisk (*), confidence interval and p-value show that the difference is statistically significant.
A similar table for diet appears in the output but we'll leave it as an exercise to the reader to interpret it.
So that's about it. I hope you were able to follow the lines of thought in this tutorial and that they make some sense to you.
SPSS Repeated Measures ANOVA Tutorial
- What is Repeated Measures ANOVA?
- Repeated Measures ANOVA Assumptions
- Quick Data Check
- Running Repeated Measures ANOVA in SPSS
- Interpreting the Output
- Reporting Repeated Measures ANOVA
1. What is Repeated Measures ANOVA?
SPSS repeated measures ANOVA tests if the means of 3 or more metric variables are all equal in some population. If this is true and we inspect a sample from our population, the sample means may differ a little bit. Large sample differences, however, are unlikely; these suggest that the population means weren't equal after all.
The simplest repeated measures ANOVA involves 3 outcome variables, all measured on 1 group of cases (often people). Whatever distinguishes these variables (sometimes just the time of measurement) is the within-subjects factor.
Repeated Measures ANOVA Example
A marketeer wants to launch a new commercial and has four concept versions. She shows the four concepts to 40 participants and asks them to rate each one of them on a 10-point scale, resulting in commercial_ratings.sav.Although such ratings are strictly ordinal variables, we'll treat them as metric variables under the assumption of equal intervals. Part of these data are shown below.

The research question is: which commercial has the highest mean rating? We'll first just inspect the mean ratings in our sample. We'll then try and generalize this sample outcome to our population by testing the null hypothesis that the 4 population mean scores are all equal. We'll reject this if our sample means are very different. Reversely, our sample means being slightly different is a normal sample outcome if population means are all similar.
2. Assumptions Repeated Measures ANOVA
Running a statistical test doesn't always make sense; results reflect reality only insofar as relevant assumptions are met. For a (single factor) repeated measures ANOVA these are
- Independent observations (or, more precisely, independent and identically distributed variables). This is often -not always- satisfied by each case in SPSS representing a different person or other statistical unit.
- The test variables follow a multivariate normal distribution in the population. However, this assumption is not needed if the sample size >= 25.
- Sphericity. This means that the population variances of all possible difference scores (com_1 - com_2, com_1 - com_3 and so on) are equal. Sphericity is tested with Mauchly’s test which is always included in SPSS’ repeated measures ANOVA output so we'll get to that later.
3. Quick Data Check
Before jumping blindly into statistical tests, let's first get a rough idea of what the data look like. Do the frequency distributions look plausible? Are there any system missing values or user missing values that we need to define? For quickly answering such questions, we'll open the data and run histograms with the syntax below.
frequencies com_1 to com_4
/format notable
/histogram.
Result
First off, our histograms look plausible and don't show any weird patterns or extreme values. There's no need to exclude any cases or define user missing values.
Second, since n = 40 for all variables, we don't have any system missing values. In this case, we can proceed with confidence.
4. Run SPSS Repeated Measures ANOVA
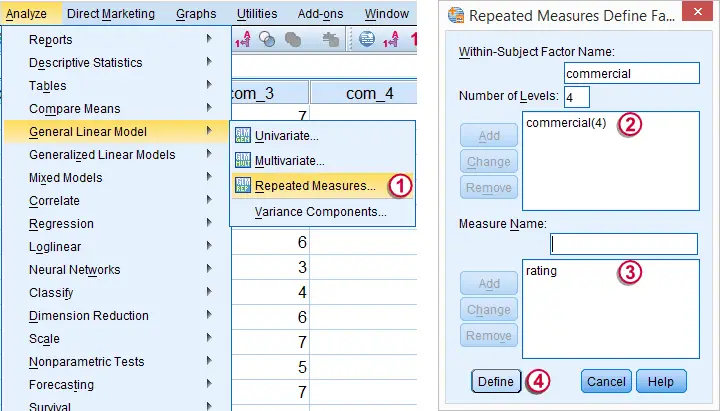
 We may freely choose a name for our within-subjects factor. We went with “commercial” because it's the commercial that differs between the four ratings made by each respondent.
We may freely choose a name for our within-subjects factor. We went with “commercial” because it's the commercial that differs between the four ratings made by each respondent.
 We may also choose a name for our measure: whatever each of the four variables is supposed to reflect. In this case we simply chose “rating”.
We may also choose a name for our measure: whatever each of the four variables is supposed to reflect. In this case we simply chose “rating”.
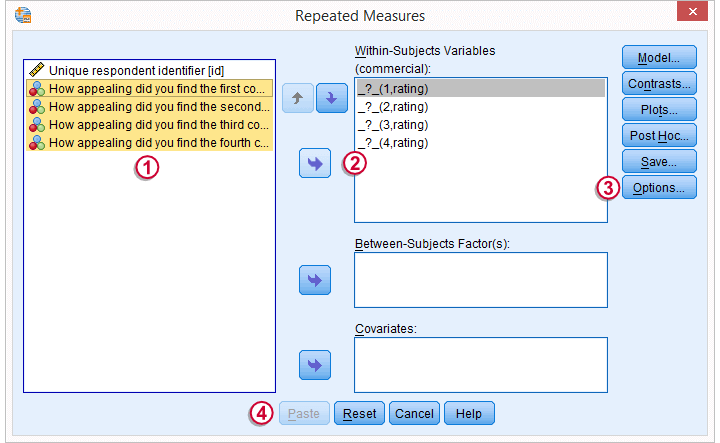
 We now select all four variables and move them to the box with
We now select all four variables and move them to the box with  the arrow to the right.
the arrow to the right.
 Under we'll select .
Under we'll select .
 Clicking results in the syntax below.
Clicking results in the syntax below.
GLM com_1 com_2 com_3 com_4
/WSFACTOR=commercial 4 Polynomial
/MEASURE=rating
/METHOD=SSTYPE(3)
/PRINT=DESCRIPTIVE
/CRITERIA=ALPHA(.05)
/WSDESIGN=commercial.
5. Repeated Measures ANOVA Output - Descriptives
First off, we take a look at the Descriptive Statistics table shown below. Commercial 4 was rated best (m = 6.25). Commercial 1 was rated worst (m = 4.15). Given our 10-point scale, these are large differences.

Repeated Measures ANOVA Output - Mauchly’s Test
We now turn to Mauchly's test for the sphericity assumption. As a rule of thumb, sphericity is assumed if Sig. > 0.05. For our data, Sig. = 0.54 so sphericity is no issue here.

The amount of sphericity is estimated by epsilon (the Greek letter ‘e’ and written as ε). There are different ways for estimating it, including the Greenhouse-Geisser, Huynh-Feldt and lower bound methods. If sphericity is violated, these are used to correct the within-subjects tests as we'll see below.If sphericity is very badly violated, we may report the Multivariate Tests table or abandon repeated measures ANOVA altogether in favor of a Friedman test.
Repeated Measures ANOVA Output - Within-Subjects Effects
Since our data seem spherical, we'll ignore the Greenhouse-Geisser, Huynh-Feldt and lower bound results in the table below. We'll simply interpret the uncorrected results denoted as “Sphericity Assumed”.

The Tests of Within-Subjects Effects is our core output. Because we've just one factor (which commercial was rated), it's pretty simple.
 Our p-value, Sig. = .000. So if the means are perfectly equal in the population, there's a 0% chance of finding the differences between the means that we observe in the sample. We therefore reject the null hypothesis of equal means.
Our p-value, Sig. = .000. So if the means are perfectly equal in the population, there's a 0% chance of finding the differences between the means that we observe in the sample. We therefore reject the null hypothesis of equal means.
 The F-value is not really interesting but we'll report it anyway. The same goes for
The F-value is not really interesting but we'll report it anyway. The same goes for  the effect degrees of freedom (df1) and
the effect degrees of freedom (df1) and  the error degrees of freedom (df2).
the error degrees of freedom (df2).
6. Reporting the Measures ANOVA Result
When reporting a basic repeated-measures ANOVA, we usually report
- the descriptive statistics table
- the outcome of Mauchly's test and
- the outcome of the within-subjects tests.
When reporting corrected results (Greenhouse-Geisser, Huynh-Feldt or lower bound), indicate which of these corrections you used. We'll cover this in SPSS Repeated Measures ANOVA - Example 2.
Finally, the main F-test is reported as
“The four commercials were not rated equally,
F(3,117) = 15.4, p = .000.”
Thank you for reading!
 SPSS TUTORIALS
SPSS TUTORIALS