SPSS Multiple Linear Regression Example
- Multiple Regression - Example
- Data Checks and Descriptive Statistics
- SPSS Regression Dialogs
- SPSS Multiple Regression Output
- Multiple Regression Assumptions
- APA Reporting Multiple Regression
Multiple Regression - Example
A scientist wants to know if and how health care costs can be predicted from several patient characteristics. All data are in health-costs.sav as shown below.
 The dependent variable is health care costs (in US dollars) declared over 2020 or “costs” for short.
The dependent variable is health care costs (in US dollars) declared over 2020 or “costs” for short.
 The independent variables are sex, age, drinking, smoking and exercise.
The independent variables are sex, age, drinking, smoking and exercise.
Our scientist thinks that each independent variable has a linear relation with health care costs. He therefore decides to fit a multiple linear regression model. The final model will predict costs from all independent variables simultaneously.
Data Checks and Descriptive Statistics
Before running multiple regression, first make sure that
- the dependent variable is quantitative;
- each independent variable is quantitative or dichotomous;
- you have sufficient sample size.
A visual inspection of our data shows that requirements 1 and 2 are met: sex is a dichotomous variable and all other relevant variables are quantitative. Regarding sample size, a general rule of thumb is that you want to
use at least 15 independent observations
for each independent variable
you'll include. In our example, we'll use 5 independent variables so we need a sample size of at least N = (5 · 15 =) 75 cases. Our data contain 525 cases so this seems fine.
 Note that we've N = 525 independent observations in our example data.
Note that we've N = 525 independent observations in our example data.
Keep in mind, however, that we may not be able to use all N = 525 cases if there's any missing values in our variables.
Let's now proceed with some quick data checks. I strongly encourage you to at least
- run basic histograms over all variables. Check if their frequency distributions look plausible. Are there any outliers? Should you specify any missing values?
- inspect a scatterplot for each independent variable (x-axis) versus the dependent variable (y-axis).A handy tool for doing just that is downloadable from SPSS - Create All Scatterplots Tool. Do you see any curvilinear relations or anything unusual?
- run descriptive statistics over all variables. Inspect if any variables have any missing values and -if so- how many.
- inspect the Pearson correlations among all variables. Absolute correlations exceeding 0.8 or so may later cause complications (known as multicollinearity) for the actual regression analysis.
The APA recommends you combine and report these last two tables as shown below.
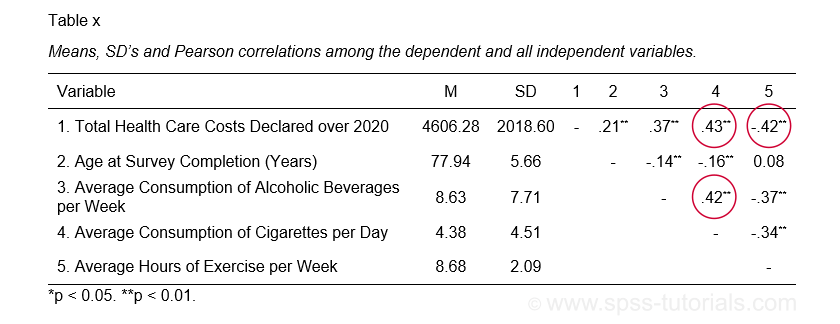 APA recommended table for reporting correlations and descriptive statistics
APA recommended table for reporting correlations and descriptive statistics as part of multiple regression results
These data checks show that our example data look perfectly fine: all charts are plausible, there's no missing values and none of the correlations exceed 0.43. Let's now proceed with the actual regression analysis.
SPSS Regression Dialogs
We'll first navigate to

 as shown below.
as shown below.
Next, we fill out the main dialog and subdialogs as shown below.
 We'll select 95% confidence intervals for our b-coefficients.
We'll select 95% confidence intervals for our b-coefficients.
 Some analysts report squared semipartial (or “part”) correlations as effect size measures for individual predictors. But for now, let's skip them.
Some analysts report squared semipartial (or “part”) correlations as effect size measures for individual predictors. But for now, let's skip them.
 By selecting “Exclude cases listwise”, our regression analysis uses only cases without any missing values on any of our regression variables. That's fine for our example data but this may be a bad idea for other data files.
By selecting “Exclude cases listwise”, our regression analysis uses only cases without any missing values on any of our regression variables. That's fine for our example data but this may be a bad idea for other data files.
 Clicking results in the syntax below. Let's run it.
Clicking results in the syntax below. Let's run it.
SPSS Multiple Regression Syntax I
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT costs
/METHOD=ENTER sex age alco cigs exer.
SPSS Multiple Regression Output
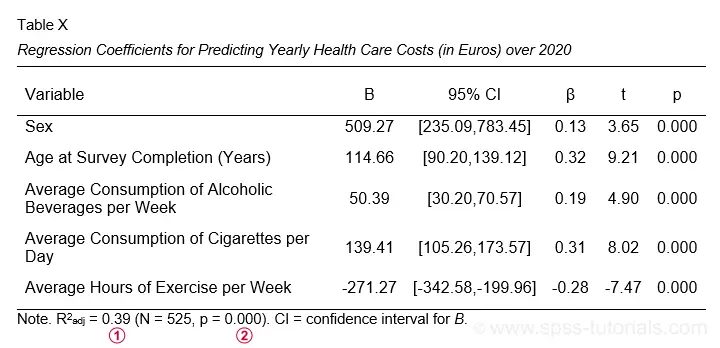
The first table we inspect is the Coefficients table shown below.
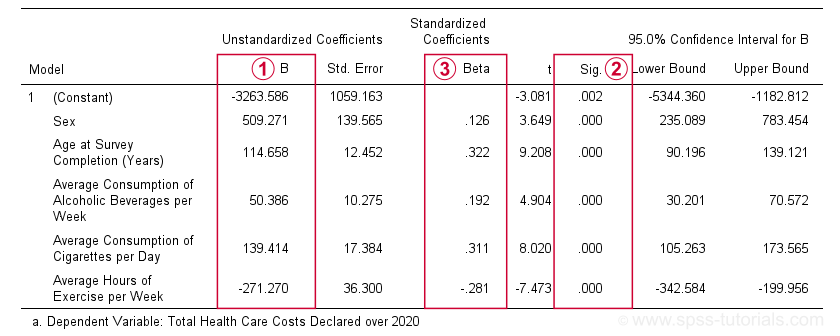
 The b-coefficients dictate our regression model:
The b-coefficients dictate our regression model:
$$Costs' = -3263.6 + 509.3 \cdot Sex + 114.7 \cdot Age + 50.4 \cdot Alcohol\\ + 139.4 \cdot Cigarettes - 271.3 \cdot Exericse$$
where \(Costs'\) denotes predicted yearly health care costs in dollars.
Each b-coefficient indicates the average increase in costs associated with a 1-unit increase in a predictor. For example, a 1-year increase in age results in an average $114.7 increase in costs. Or a 1 hour increase in exercise per week is associated with a -$271.3 increase (that is, a $271.3 decrease) in yearly health costs.
Now, let's talk about sex: a 1-unit increase in sex results in an average $509.3 increase in costs. For understanding what this means, please note that sex is coded 0 (female) and 1 (male) in our example data. So for this variable, the only possible 1-unit increase is from female (0) to male (1). Therefore, B = $509.3 simply means that
the average yearly costs for males
are $509.3 higher than for females
(everything else equal, that is). This hopefully clarifies how dichotomous variables can be used in multiple regression. We'll expand on this idea when we'll cover dummy variables in a later tutorial.
 The “Sig.” column in our coefficients table contains the (2-tailed) p-value for each b-coefficient. As a general guideline,
a b-coefficient is statistically significant if its “Sig.” or p < 0.05.
Therefore, all b-coefficients in our table are highly statistically significant. Precisely, a p-value of 0.000 means that if some b-coefficient is zero in the population (the null hypothesis), then there's a 0.000 probability of finding the observed sample b-coefficient or a more extreme one. We then conclude that the population b-coefficient probably wasn't zero after all.
The “Sig.” column in our coefficients table contains the (2-tailed) p-value for each b-coefficient. As a general guideline,
a b-coefficient is statistically significant if its “Sig.” or p < 0.05.
Therefore, all b-coefficients in our table are highly statistically significant. Precisely, a p-value of 0.000 means that if some b-coefficient is zero in the population (the null hypothesis), then there's a 0.000 probability of finding the observed sample b-coefficient or a more extreme one. We then conclude that the population b-coefficient probably wasn't zero after all.
Now, our b-coefficients don't tell us the relative strengths of our predictors. This is because these have different scales: is a cigarette per day more or less than an alcoholic beverage per week? One way to deal with this, is to compare the standardized regression coefficients or beta coefficients, often denoted as β (the Greek letter “beta”).In statistics, β also refers to the probability of committing a type II error in hypothesis testing. This is why (1 - β) denotes power but that's a completely different topic than regression coefficients.
 Beta coefficients (standardized regression coefficients) are useful for comparing the relative strengths of our predictors. Like so, the 3 strongest predictors in our coefficients table are:
Beta coefficients (standardized regression coefficients) are useful for comparing the relative strengths of our predictors. Like so, the 3 strongest predictors in our coefficients table are:
- age (β = 0.322);
- cigarette consumption (β = 0.311);
- exercise (β = -0.281).
Beta coefficients are obtained by standardizing all regression variables into z-scores before computing b-coefficients. Standardizing variables applies a similar standard (or scale) to them: the resulting z-scores always have mean of 0 and a standard deviation of 1.
This holds regardless whether they're computed over years, cigarettes or alcoholic beverages. So that's why b-coefficients computed over standardized variables -beta coefficients- are comparable within and between regression models.
Right, so our b-coefficients make up our multiple regression model. This tells us how to predict yearly health care costs. What we don't know, however, is precisely how well does our model predict these costs? We'll find the answer in the model summary table discussed below.
SPSS Regression Output II - Model Summary & ANOVA
The figure below shows  the model summary and
the model summary and  the ANOVA tables in the regression output.
the ANOVA tables in the regression output.

 R denotes the multiple correlation coefficient. This is simply the Pearson correlation between the actual scores and those predicted by our regression model.
R denotes the multiple correlation coefficient. This is simply the Pearson correlation between the actual scores and those predicted by our regression model.
 R-square or R2 is simply the squared multiple correlation. It is also the proportion of variance in the dependent variable accounted for by the entire regression model.
R-square or R2 is simply the squared multiple correlation. It is also the proportion of variance in the dependent variable accounted for by the entire regression model.
 R-square computed on sample data tends to overestimate R-square for the entire population. We therefore prefer to report adjusted R-square or R2adj, which is an unbiased estimator for the population R-square. For our example, R2adj = 0.390. By most standards, this is considered very high.
R-square computed on sample data tends to overestimate R-square for the entire population. We therefore prefer to report adjusted R-square or R2adj, which is an unbiased estimator for the population R-square. For our example, R2adj = 0.390. By most standards, this is considered very high.
Sadly, SPSS doesn't include a confidence interval for R2adj. However, the p-value found in the ANOVA table applies to R and R-square (the rest of this table is pretty useless). It evaluates the null hypothesis that our entire regression model has a population R of zero. Since p < 0.05, we reject this null hypothesis for our example data.
It seems we're done for this analysis but we skipped an important step: checking the multiple regression assumptions.
Multiple Regression Assumptions
Our data checks started off with some basic requirements. However, the “official” multiple linear regression assumptions are
- independent observations;
- normality: the regression residuals must be normally distributed in the populationStrictly, we should distinguish between residuals (sample) and errors (population). For now, however, let's not overcomplicate things.;
- homoscedasticity: the population variance of the residuals should not fluctuate in any systematic way;
- linearity: each predictor must have a linear relation with the dependent variable.
We'll check if our example analysis meets these assumptions by doing 3 things:
- A visual inspection of our data shows that each of our N = 525 observations applies to a different person. Furthermore, these people did not interact in any way that should influence their survey answers. In this case, we usually consider them independent observations.
- We'll create and inspect a histogram of our regression residuals to see if they are approximately normally distributed.
- We'll create and inspect a scatterplot of residuals (y-axis) versus predicted values (x-axis). This scatterplot may detect violations of both homoscedasticity and linearity.
The easy way to obtain these 2 regression plots, is selecting them in the dialogs (shown below) and rerunning the regression analysis.
 Clicking results in the syntax below. We'll run it and inspect the residual plots shown below.
Clicking results in the syntax below. We'll run it and inspect the residual plots shown below.
SPSS Multiple Regression Syntax II
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT costs
/METHOD=ENTER sex age alco cigs exer
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
Residual Plots I - Histogram
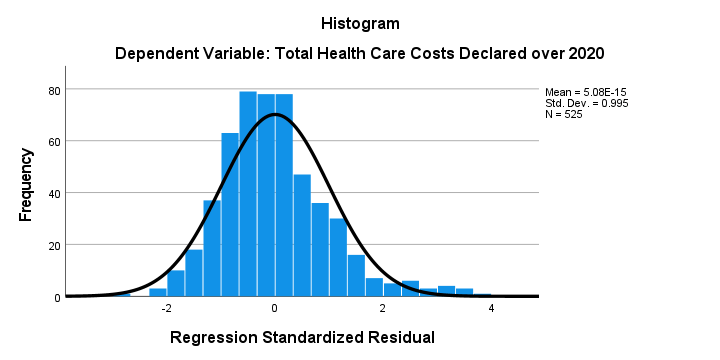
The histogram over our standardized residuals shows
- a tiny bit of positive skewness; the right tail of the distribution is stretched out a bit.
- a tiny bit of positive kurtosis; our distribution is more peaked (or “leptokurtic”) than the normal curve. This is because the bars in the middle are too high and pierce through the normal curve.
In short, we do see some deviations from normality but they're tiny. Most analysts would conclude that the residuals are roughly normally distributed. If you're not convinced, you could add the residuals as a new variable to the data via the SPSS regression dialogs. Next, you could run a Shapiro-Wilk test or a Kolmogorov-Smirnov test on them. However, we don't generally recommend these tests.
Residual Plots II - Scatterplot
The residual scatterplot shown below is often used for checking a) the homoscedasticity and b) the linearity assumptions. If both assumptions hold, this scatterplot shouldn't show any systematic pattern whatsoever. That seems to be the case here.
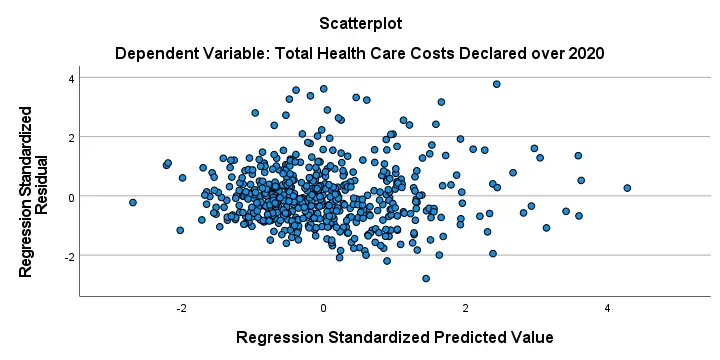
Homoscedasticity implies that the variance of the residuals should be constant. This variance can be estimated from how far the dots in our scatterplot lie apart vertically. Therefore, the height of our scatterplot should neither increase nor decrease as we move from left to right. We don't see any such pattern.
A common check for the linearity assumption is inspecting if the dots in this scatterplot show any kind of curve. That's not the case here so linearity also seems to hold here.On a personal note, however, I find this a very weak approach. An unusual (but much stronger) approach is to fit a variety of non linear regression models for each predictor separately.
Doing so requires very little effort and often reveils non linearity. This can then be added to some linear model in order to improve its predictive accuracy.
Sadly, this “low hanging fruit” is routinely overlooked because analysts usually limit themselves to the poor scatterplot aproach that we just discussed.
APA Reporting Multiple Regression
The APA reporting guidelines propose the table shown below for reporting a standard multiple regression analysis.
I think it's utter stupidity that the APA table doesn't include the constant for our regression model. I recommend you add it anyway. Furthermore, note that
 R-square adjusted is found in the model summary table and
R-square adjusted is found in the model summary table and
 its p-value is the only number you need from the ANOVA table
its p-value is the only number you need from the ANOVA table
in the SPSS output. Last, the APA also recommends reporting a combined descriptive statistics and correlations table like we saw here.
Thanks for reading!
SPSS Scatterplots & Fit Lines Tool
Contents
- Example Data File
- Prerequisites and Installation
- Example I - Create All Unique Scatterplots
- Example II - Linearity Checks for Predictors
Visualizing your data is the single best thing you can do with it. Doing so may take little effort: a single line FREQUENCIES command in SPSS can create many histograms or bar charts in one go.
Sadly, the situation for scatterplots is different: each of them requires a separate command. We therefore built a tool for creating one, many or all scatterplots among a set of variables, optionally with (non)linear fit lines and regression tables.
Example Data File
We'll use health-costs.sav (partly shown below) throughout this tutorial.

We encourage you to download and open this file and replicate the examples we'll present in a minute.
Prerequisites and Installation
Our tool requires SPSS version 24 or higher. Also, the SPSS Python 3 essentials must be installed (usually the case with recent SPSS versions).
Clicking SPSS_TUTORIALS_SCATTERS.spe downloads our scatterplots tool. You can install it through as shown below.
In the dialog that opens, navigate to the downloaded .spe file and install it. SPSS will then confirm that the extension was successfully installed under

Example I - Create All Unique Scatterplots
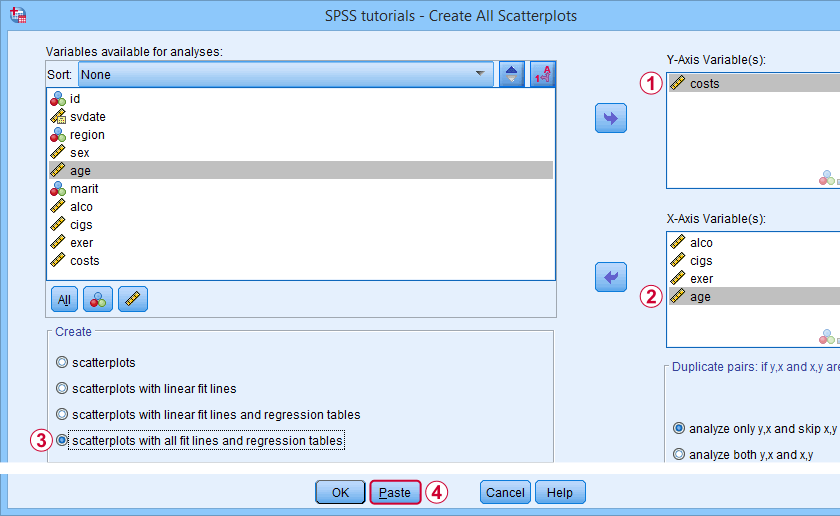
Let's now inspect all unique scatterplots among health costs, alcohol and cigarette consumption and exercise. We'll navigate to and fill out the dialog as shown below.
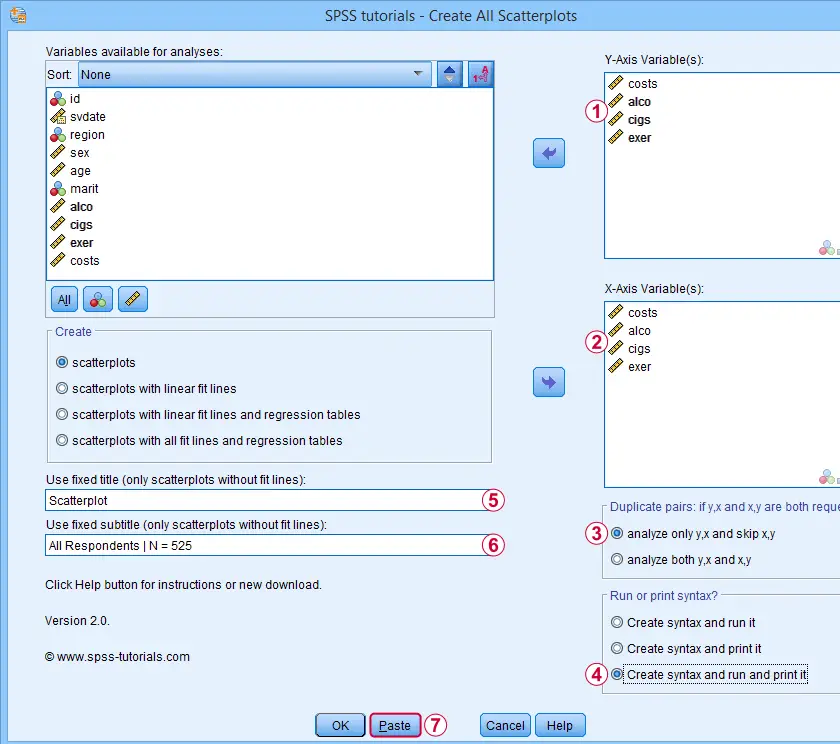
 We enter all relevant variables as y-axis variables. We recommend you always first enter the dependent variable (if any).
We enter all relevant variables as y-axis variables. We recommend you always first enter the dependent variable (if any).
 We enter these same variables as x-axis variables.
We enter these same variables as x-axis variables.
 This combination of y-axis and x-axis variables results in duplicate chart. For instance, costs by alco is similar alco by costs transposed. Such duplicates are skipped if “analyze only y,x and skip x,y” is selected.
This combination of y-axis and x-axis variables results in duplicate chart. For instance, costs by alco is similar alco by costs transposed. Such duplicates are skipped if “analyze only y,x and skip x,y” is selected.
 Besides creating scatterplots, we'll also take a quick look at the SPSS syntax that's generated.
Besides creating scatterplots, we'll also take a quick look at the SPSS syntax that's generated.
 If no title is entered, our tool applies automatic titles. For this example, the automatic titles were rather lengthy. We therefore override them with a fixed title (“Scatterplot”) for all charts. The only way to have no titles at all is suppressing them with a chart template.
If no title is entered, our tool applies automatic titles. For this example, the automatic titles were rather lengthy. We therefore override them with a fixed title (“Scatterplot”) for all charts. The only way to have no titles at all is suppressing them with a chart template.
 Clicking results in the syntax below. Let's run it.
Clicking results in the syntax below. Let's run it.
SPSS Scatterplots Tool - Syntax I
SPSS TUTORIALS SCATTERS YVARS=costs alco cigs exer XVARS=costs alco cigs exer
/OPTIONS ANALYSIS=SCATTERS ACTION=BOTH TITLE="Scatterplot" SUBTITLE="All Respondents | N = 525".
Results
First off, note that the GRAPH commands that were run by our tool have also been printed in the output window (shown below). You could copy, paste, edit and run these on any SPSS installation, even if it doesn't have our tool installed.
Beneath this syntax, we find all 6 unique scatterplots. Most of them show substantive correlations and all of them look plausible. However, do note that some plots -especially the first one- hint at some curvilinearity. We'll thoroughly investigate this in our second example.
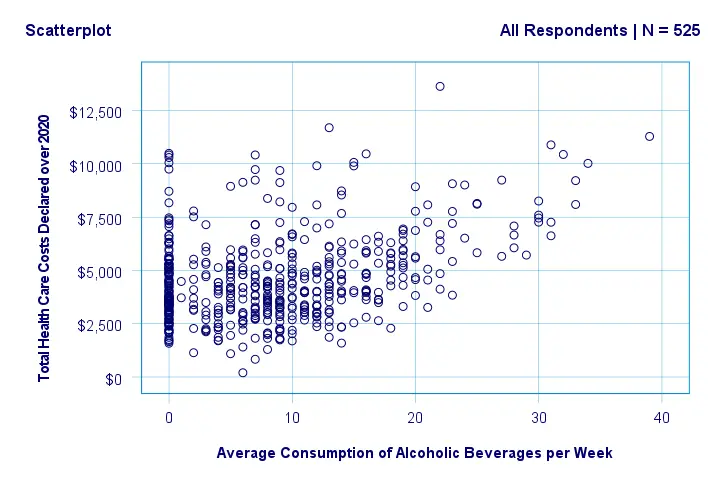
In any case, we feel that a quick look at such scatterplots should always precede an SPSS correlation analysis.
Example II - Linearity Checks for Predictors
I'd now like to run a multiple regression analysis for predicting health costs from several predictors. But before doing so, let's see if each predictor relates linearly to our dependent variable. Again, we navigate to and fill out the dialog as shown below.
 Our dependent variable is our y-axis variable.
Our dependent variable is our y-axis variable.
 All independent variables are x-axis variables.
All independent variables are x-axis variables.
 We'll create scatterplots with all fit lines and regression tables.
We'll create scatterplots with all fit lines and regression tables.
 We'll run the syntax below after clicking the button.
We'll run the syntax below after clicking the button.
SPSS Scatterplots Tool - Syntax II
SPSS TUTORIALS SCATTERS YVARS=costs XVARS=alco cigs exer age
/OPTIONS ANALYSIS=FITALLTABLES ACTION=RUN.
Note that running this syntax triggers some warnings about zero values in some variables. These can safely be ignored for these examples.
Results
In our first scatterplot with regression lines, some curves deviate substantially from linearity as shown below.
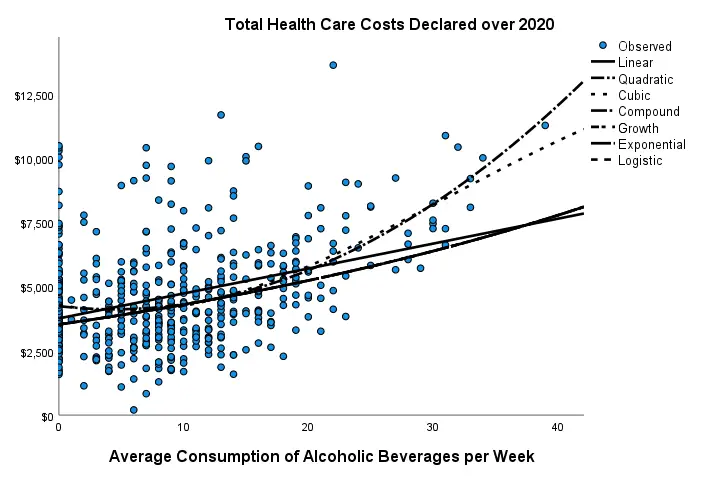
Sadly, this chart's legend doesn't quite help to identify which curve visualizes which transformation function. So let's look at the regression table shown below.
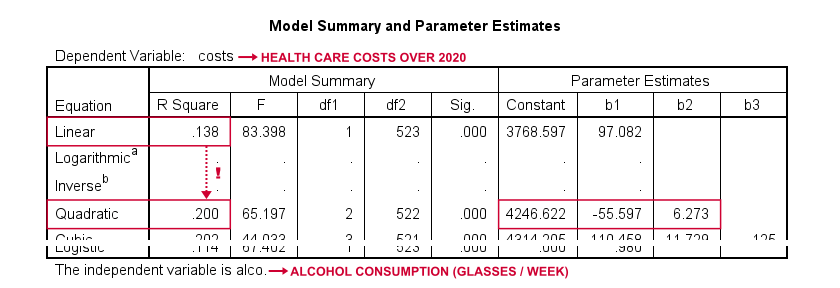
Very interestingly, r-square skyrockets from 0.138 to 0.200 when we add the squared predictor to our model. The b-coefficients tell us that the regression equation for this model is Costs’ = 4,246.22 - 55.597 * alco + 6.273 * alco2 Unfortunately, this table doesn't include significance levels or confidence intervals for these b-coefficients. However, these are easily obtained from a regression analysis after adding the squared predictor to our data. The syntax below does just that.
compute alco2 = alco**2.
*Multiple regression for costs on squared and non squared alcohol consumption.
regression
/statistics r coeff ci(95)
/dependent costs
/method enter alco alco2.
Result
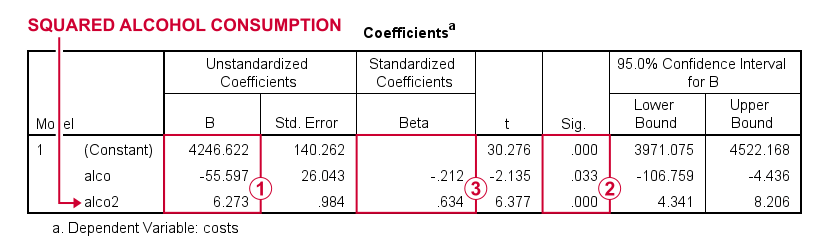
 First note that we replicated the exact b-coefficients we saw earlier.
First note that we replicated the exact b-coefficients we saw earlier.
 Surprisingly, our squared predictor is more statistically significant than its original, non squared counterpart.
Surprisingly, our squared predictor is more statistically significant than its original, non squared counterpart.
 The beta coefficients suggest that the relative strength of the squared predictor is roughly 3 times that of the original predictor.
The beta coefficients suggest that the relative strength of the squared predictor is roughly 3 times that of the original predictor.
In short, these results suggest substantial non linearity for at least one predictor. Interestingly, this is not detected by using the standard linearity check: inspecting a scatterplot of standardized residuals versus predicted values after running multiple regression.
But anyway, I just wanted to share the tool I built for these analyses and illustrate it with some typical examples. Hope you found it helpful!
If you've any feedback, we always appreciate if you throw us a comment below.
Thanks for reading!
SPSS Hierarchical Regression Tutorial
Hierarchical regression comes down to comparing different regression models. Each model adds 1(+) predictors to the previous model, resulting in a “hierarchy” of models. This analysis is easy in SPSS but we should pay attention to some regression assumptions:
- linearity: each predictor has a linear relation with our outcome variable;
- normality: the prediction errors are normally distributed in the population;
- homoscedasticity: the variance of the errors is constant in the population.
Also, let's ensure our data make sense in the first place and choose which predictors we'll include in our model. The roadmap below summarizes these steps.
SPSS Hierarchical Regression Roadmap
| Step | Why? | Action? | |
|---|---|---|---|
| 1 | Inspect histograms | See if distributions make sense. | Set missing values. Exclude variables. |
| 2 | Inspect descriptives | See if any variables have low N. Inspect listwise valid N. | Exclude variables with low N. |
| 3 | Inspect scatterplots | See if relations are linear. Look for influential cases. | Exclude cases if needed. Transform predictors if needed. |
| 4 | Inspect correlation matrix | See if Pearson correlations make sense. | Inspect variables with unusual correlations. |
| 5 | Regression I: model selection | See which model is good. | Exclude variables from model. |
| 6 | Regression II: residuals | Inspect residual plots. | Transform variables if needed. |
Case Study - Employee Satisfaction
A company held an employee satisfaction survey which included overall employee satisfaction. Employees also rated some main job quality aspects, resulting in work.sav.
The main question we'd like to answer is which quality aspects predict job satisfaction? Let's follow our roadmap and find out.
Inspect All Histograms
Let's first see if our data make any sense in the first place. We'll do so by running histograms over all predictors and the dependent variable. The easiest way for doing so is running the syntax below. For more detailed instructions, see Creating Histograms in SPSS.
frequencies overall to tasks
/format notable
/histogram.
Result
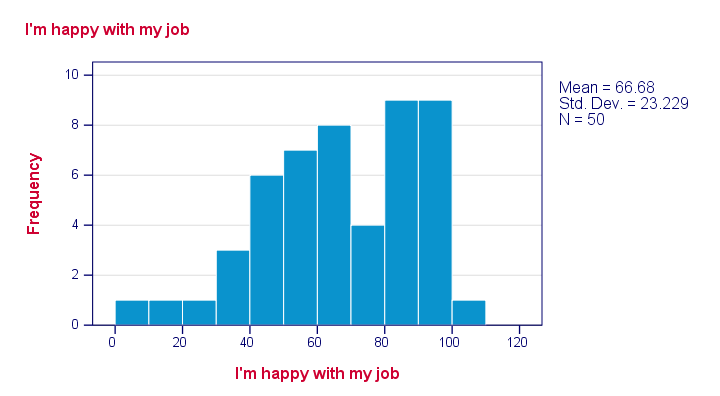
Just a quick look at our 6 histograms tells us that
- none of these variables contain any system missing values;
- none of our variables contain any clear outliers: there's no need to set any user missing values;
- all frequency distributions look plausible.
If histograms do show unlikely values, it's essential to set those as user missing values before proceeding with your analyses.
Inspect Descriptives Table
If variables contain missing values, a simple descriptives table is a fast way to inspect the extent of missingness. We'll run it from a single line of syntax .
descriptives overall to tasks.
Result
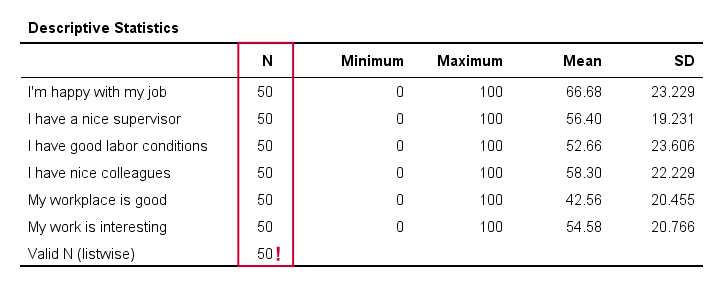
The descriptives table tells us if any variables have many missing values. If so, you may want to exclude such variables from analysis.
Valid N (listwise) is the number of cases without missing values on any variables in this table. SPSS regression (as well as factor analysis) uses only such complete cases unless you select pairwise deletion of missing values as we'll see in a minute.
Inspect Scatterplots
Do our predictors have (roughly) linear relations with the outcome variable? Most textbooks suggest inspecting residual plots: scatterplots of the predicted values (x-axis) with the residuals (y-axis) are supposed to detect non linearity.
However, I think residual plots are useless for inspecting linearity. The reason is that predicted values are (weighted) combinations of predictors. So what if just one predictor has a curvilinear relation with the outcome variable? This curvilinearity will be diluted by combining predictors into one variable -the predicted values.
It makes much more sense to inspect linearity for each predictor separately. A minimal way to do so is running scatterplots for each predictor (x-axis) with the outcome variable (y-axis).
A simple way to create these scatterplots is to just one command from the menu as shown in SPSS Scatterplot Tutorial. Next, remove the line breaks and copy-paste-edit it as needed.
GRAPH /SCATTERPLOT(BIVAR)= supervisor WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= conditions WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= colleagues WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= workplace WITH overall /MISSING=LISTWISE.
GRAPH /SCATTERPLOT(BIVAR)= tasks WITH overall /MISSING=LISTWISE.
Result
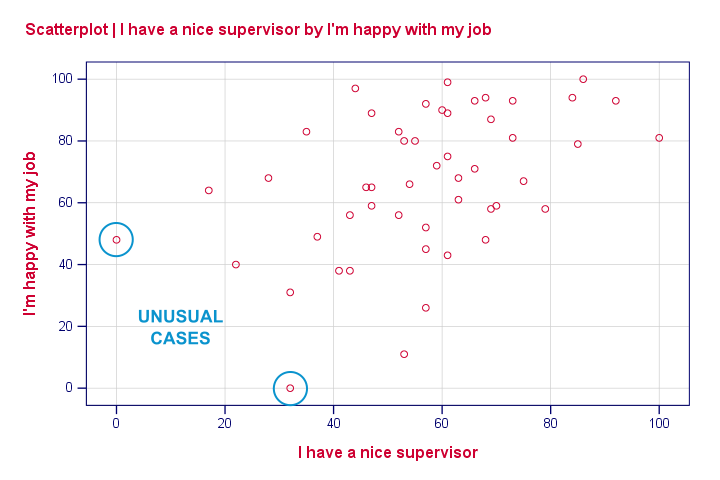
None of our scatterplots show clear curvilinearity. However, we do see some unusual cases that don't quite fit the overall pattern of dots. We'll flag and inspect these cases with the syntax below.
compute flag1 = (overall > 40 and supervisor < 10).
*Move unusual case(s) to top of file for visual inspection.
sort cases by flag1(d).
Result
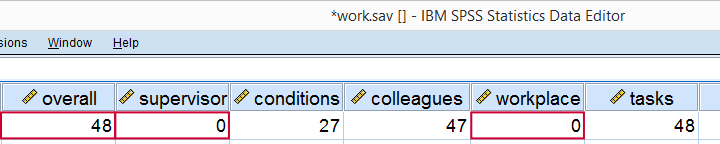
Our first case looks odd indeed: supervisor and workplace are 0 -couldn't be worse- but overall job rating is quite good. We should perhaps exclude such cases from further analyses with FILTER but we'll just ignore them for now.
Regarding linearity, our scatterplots provide a minimal check. A much better approach is inspecting linear and nonlinear fit lines as discussed in How to Draw a Regression Line in SPSS?
An excellent tool for doing this super fast and easy is downloadable from SPSS - Create All Scatterplots Tool.
Inspect Correlation Matrix
We'll now see if the (Pearson) correlations among all variables make sense. For the data at hand, I'd expect only positive correlations between, say, 0.3 and 0.7 or so. For more details, read up on SPSS Correlation Analysis.
correlations overall to tasks
/print nosig
/missing pairwise.
Result
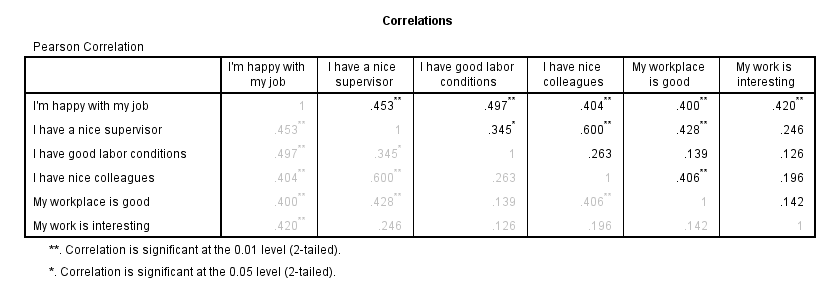
The pattern of correlations looks perfectly plausible. Creating a nice and clean correlation matrix like this is covered in SPSS Correlations in APA Format.
Regression I - Model Selection
The next question we'd like to answer is:
which predictors contribute substantially
to predicting job satisfaction?
Our correlations show that all predictors correlate statistically significantly with the outcome variable. However, there's also substantial correlations among the predictors themselves. That is, they overlap.
Some variance in job satisfaction accounted by a predictor may also be accounted for by some other predictor. If so, this other predictor may not contribute uniquely to our prediction.
There's different approaches towards finding the right selection of predictors. One of those is adding all predictors one-by-one to the regression equation. Since we've 5 predictors, this will result in 5 models. So let's navigate to and fill out the dialog as shown below.
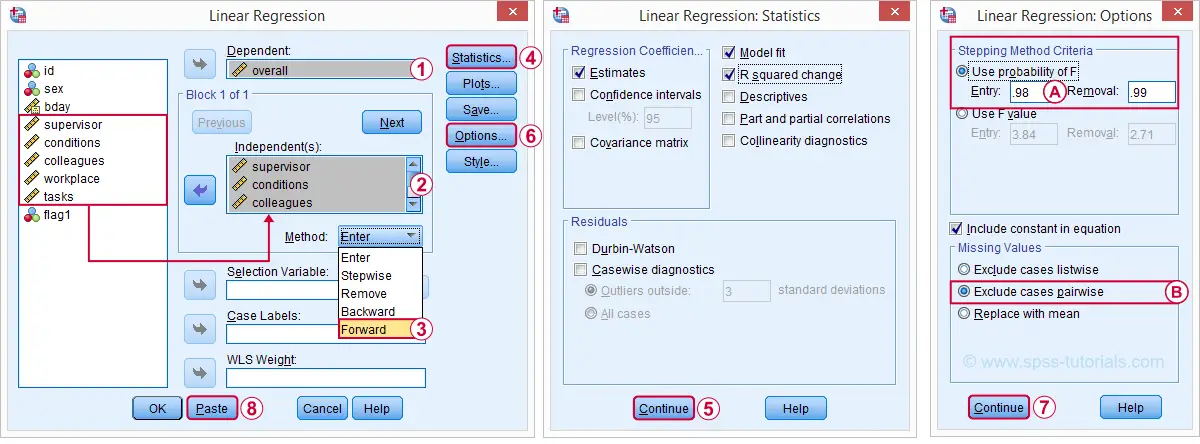
 The method we chose means that SPSS will add all predictors (one at the time) whose p-valuesPrecisely, this is the p-value for the null hypothesis that the population b-coefficient is zero for this predictor. are less than some chosen constant, usually 0.05.
The method we chose means that SPSS will add all predictors (one at the time) whose p-valuesPrecisely, this is the p-value for the null hypothesis that the population b-coefficient is zero for this predictor. are less than some chosen constant, usually 0.05.
 Choosing 0.98 -or even higher- usually results in all predictors being added to the regression equation.
Choosing 0.98 -or even higher- usually results in all predictors being added to the regression equation.
 By default, SPSS uses only cases without missing values on the predictors and the outcome variable (“listwise exclusion”). If missing values are scattered over variables, this may result in little data actually being used for the analysis. For cases with missing values, pairwise exclusion tries to use all non missing values for the analysis.Pairwise deletion is not uncontroversial and may occasionally result in computational problems.
By default, SPSS uses only cases without missing values on the predictors and the outcome variable (“listwise exclusion”). If missing values are scattered over variables, this may result in little data actually being used for the analysis. For cases with missing values, pairwise exclusion tries to use all non missing values for the analysis.Pairwise deletion is not uncontroversial and may occasionally result in computational problems.
Syntax Regression I - Model Selection
REGRESSION
/MISSING PAIRWISE /*... because LISTWISE uses only complete cases...*/
/STATISTICS COEFF OUTS R ANOVA CHANGE
/CRITERIA=PIN(.98) POUT(.99)
/NOORIGIN
/DEPENDENT overall
/METHOD=FORWARD supervisor conditions colleagues workplace tasks.
Results Regression I - Model Summary
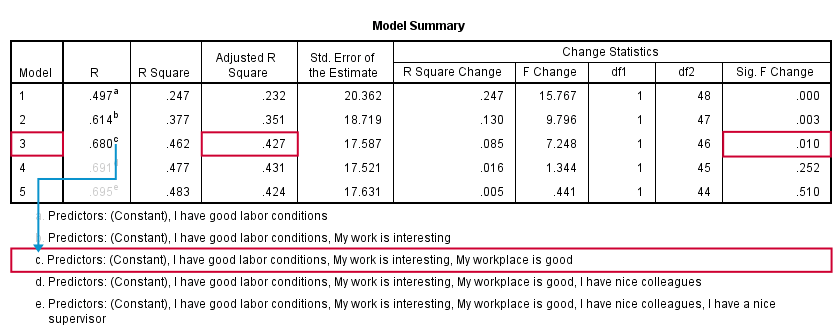
SPSS fitted 5 regression models by adding one predictor at the time. The model summary table shows some statistics for each model. The adjusted r-square column shows that it increases from 0.351 to 0.427 by adding a third predictor.
However, r-square adjusted hardly increases any further by adding a fourth predictor and it even decreases when we enter a fifth predictor. There's no point in including more than 3 predictors in or model. The “Sig. F Change” column confirms this: the increase in r-square from adding a third predictor is statistically significant, F(1,46) = 7.25, p = 0.010. Adding a fourth predictor does not significantly improve r-square any further. In short: this table suggests we should choose model 3.
Results Regression I - B Coefficients
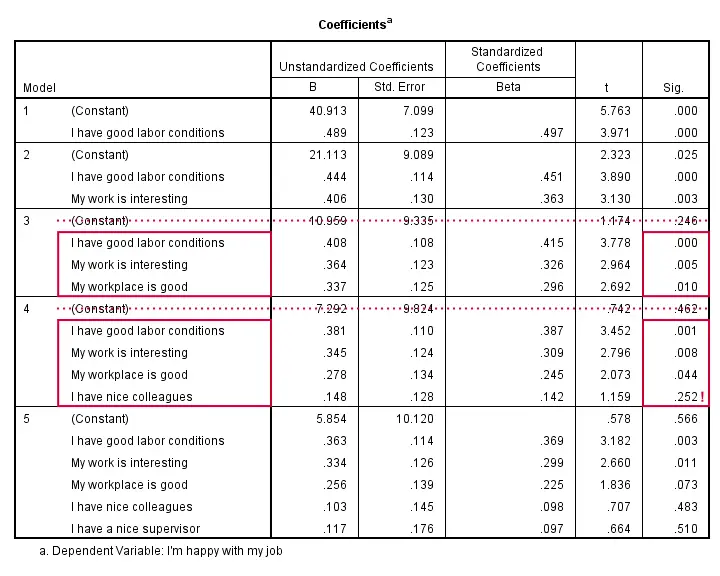
The coefficients table shows that all b-coefficients for model 3 are statistically significant. For a fourth predictor, p = 0.252. Its b-coefficient of 0.148 is not statistically significant. That is, it may well be zero in our population. Realistically, we can't take b = 0.148 seriously. We should not use it for predicting job satisfaction. It's not unlikely to deteriorate -rather than improve- predictive accuracy except for this tiny sample of N = 50.
Note that all b-coefficients shrink as we add more predictors. If we include 5 predictors (model 5), only 2 are statistically significant. The b-coefficients become unreliable if we estimate too many of them.
A rule of thumb is that we need 15 observations for each predictor. With N = 50, we should not include more than 3 predictors and the coefficients table shows exactly that. Conclusion? We settle for model 3 which says that
Satisfaction’ = 10.96 + 0.41 * conditions
+ 0.36 * interesting + 0.34 * workplace.
Now, before we report this model, we should take a close look if our regression assumptions are met. We usually do so by inspecting regression residual plots.
Regression II - Residual Plots
Let's reopen our regression dialog. An easy way is to use the dialog recall ![]() tool on our toolbar. Since model 3 excludes supervisor and colleagues, we'll remove them from the model as shown below.
tool on our toolbar. Since model 3 excludes supervisor and colleagues, we'll remove them from the model as shown below.
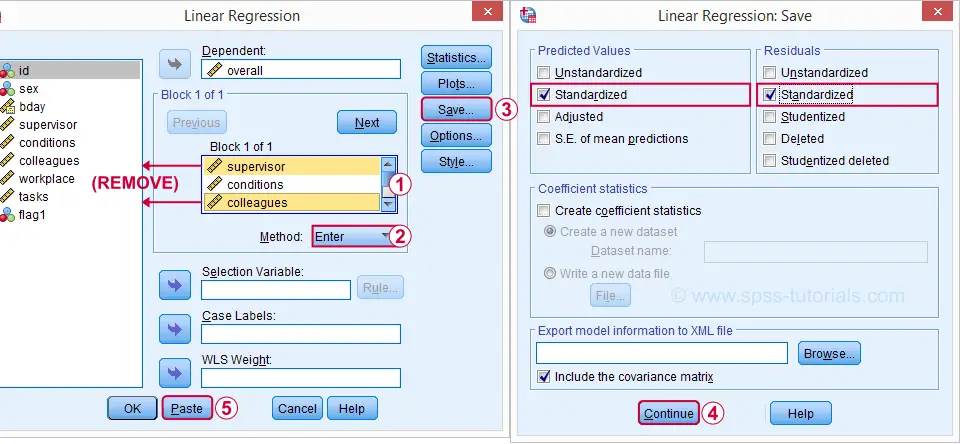
Now, the regression dialogs can create some residual plots but I rather do this myself. This is fairly easy if we  save the predicted values and residuals as new variables in our data.
save the predicted values and residuals as new variables in our data.
Syntax Regression II - Residual Plots
REGRESSION
/MISSING PAIRWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA CHANGE /*CI(95) = 95% confidence intervals for B coefficients.*
/CRITERIA=PIN(.98) POUT(.99)
/NOORIGIN
/DEPENDENT overall
/METHOD=ENTER conditions workplace tasks /*Only 3 predictors now.*
/SAVE ZPRED ZRESID.
Results Regression II - Normality Assumption
First note that SPSS added two new variables to our data: ZPR_1 holds z-scores for our predicted values. ZRE_1 are standardized residuals.
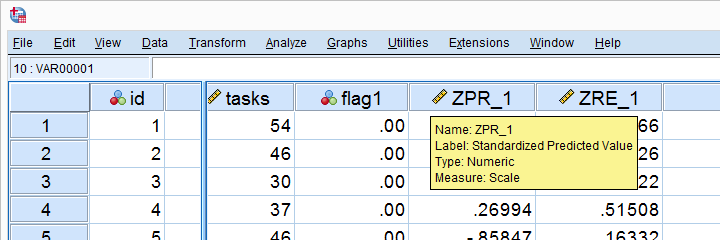
Let's first see if the residuals are normally distributed. We'll do so with a quick histogram.
frequencies zre_1
/format notable
/histogram normal.
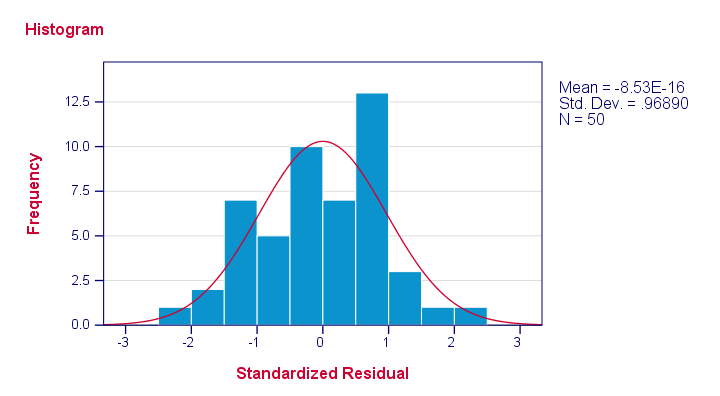
Note that our residuals are roughly normally distributed.
Results Regression II - Linearity and Homoscedasticity
Let's now see to what extent homoscedasticity holds. We'll create a scatterplot for our predicted values (x-axis) with residuals (y-axis).
GRAPH
/SCATTERPLOT(BIVAR)= zpr_1 WITH zre_1
/title "Scatterplot for evaluating homoscedasticity and linearity".
Result
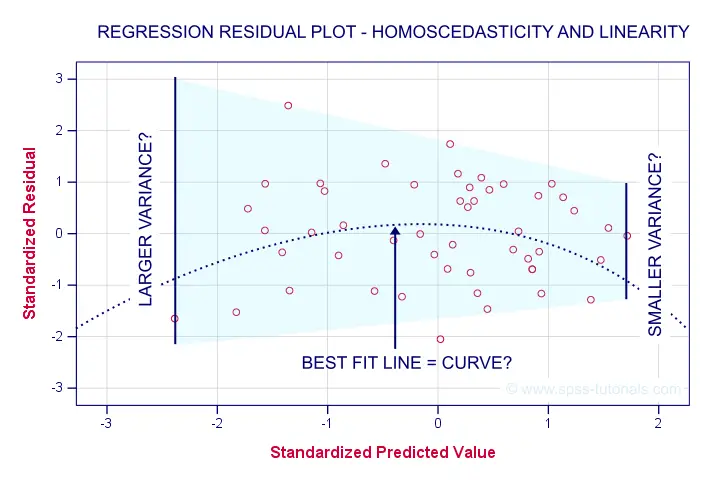
First off, our dots seem to be less dispersed vertically as we move from left to right. That is: the residual variance seems to decrease with higher predicted values. This pattern is known as heteroscedasticity and suggests a (slight) violation of the homoscedasticity assumption.
Second, our dots seem to follow a somewhat curved -rather than straight or linear- pattern. It may be wise to try and fit some curvilinear models to these data but let's leave that for another day.
Right, that should do for now. Some guidelines on APA reporting multiple regression results are discussed in Linear Regression in SPSS - A Simple Example.
Thanks for reading!
SPSS Mediation Analysis – The Complete Guide
- How to Examine Mediation Effects?
- SPSS Regression Dialogs
- SPSS Mediation Analysis Output
- APA Reporting Mediation Analysis
- Next Steps - The Sobel Test
- Next Steps - Index of Mediation
Example
A scientist wants to know which factors affect general well-being among people suffering illnesses. In order to find out, she collects some data on a sample of N = 421 cancer patients. These data -partly shown below- are in wellbeing.sav.
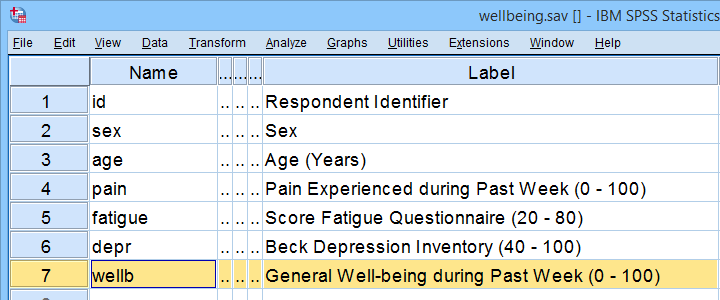
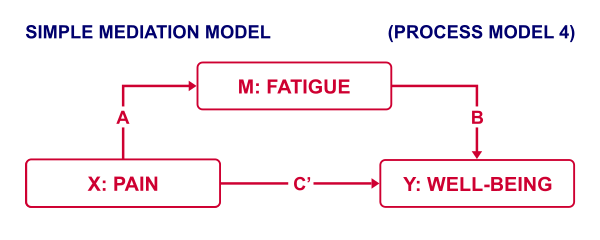
Now, our scientist believes that well-being is affected by pain as well as fatigue. On top of that, she believes that fatigue itself is also affected by pain. In short: pain partly affects well-being through fatigue. That is, fatigue mediates the effect from pain onto well-being as illustrated below.
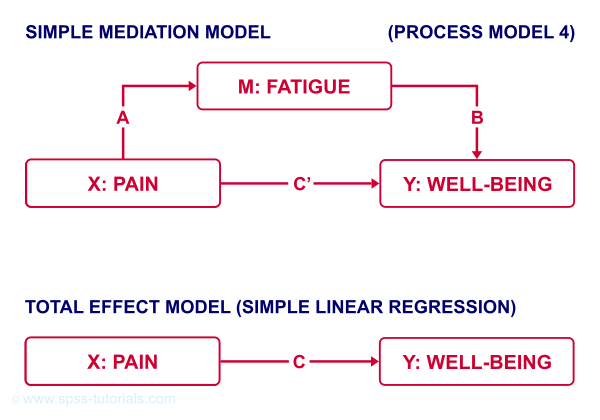
The lower half illustrates a model in which fatigue would (erroneously) be left out. This is known as the “total effect model” and is often compared with the mediation model above it.
How to Examine Mediation Effects?
Now, let's suppose for a second that all expectations from our scientist are exactly correct. If so, then what should we see in our data? The classical approach to mediation (see Kenny & Baron, 1986) says that
- \(a\) (from pain to fatigue) should be significant;
- \(b\) (from fatigue to well-being) should be significant;
- \(c\) (from pain to well-being) should be significant;
- \(c\,'\) (direct effect) should be closer to zero than \(c\) (total effect).
So how to find out if our data is in line with these statements? Well, all paths are technically just b-coefficients. We'll therefore run 3 (separate) regression analyses:
- regression from pain onto fatigue tells us if \(a\) is significant;
- multiple linear regression from pain and fatigue onto well-being tells us if \(b\) and \(c\,'\) are significant;
- regression from pain onto well-being tells if \(c\) is significant and/or different from \(c\,'\).
 Paths c’ and b in basic SPSS regression output
Paths c’ and b in basic SPSS regression output
SPSS Regression Dialogs
So let's first run the regression analysis for effect \(a\) (X onto mediator) in SPSS: we'll open wellbeing.sav and navigate to the linear regression dialogs as shown below.

For a fairly basic analysis, we'll fill out these dialogs as shown below.
Completing these steps results in the SPSS syntax below. I suggest you shorten the pasted version a bit.
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95) R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT fatigue /* MEDIATOR */
/METHOD=ENTER pain /* X */
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
*SHORTEN TO SOMETHING LIKE...
REGRESSION
/STATISTICS COEFF CI(95) R
/DEPENDENT fatigue /* MEDIATOR */
/METHOD=ENTER pain /* X */
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
A second regression analysis estimates effects \(b\) and \(c\,'\). The easiest way to run it is to copy, paste and edit the first syntax as shown below.
REGRESSION
/STATISTICS COEFF CI(95) R
/DEPENDENT wellb /* Y */
/METHOD=ENTER pain fatigue /* X AND MEDIATOR */
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
We'll use the syntax below for the third (and final) regression which estimates \(c\), the total effect.
REGRESSION
/STATISTICS COEFF CI(95) R
/DEPENDENT wellb /* Y */
/METHOD=ENTER pain /* X */
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
SPSS Mediation Analysis Output
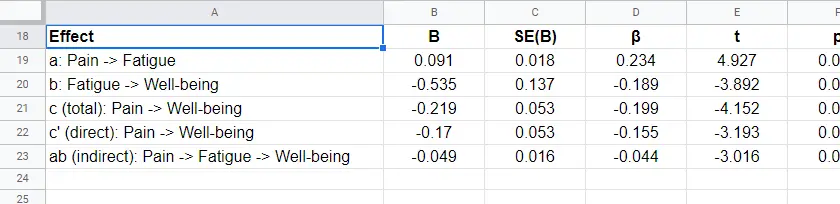
For our mediation analysis, we really only need the 3 coefficients tables. I copy-pasted them into this Googlesheet (read-only, partly shown below).
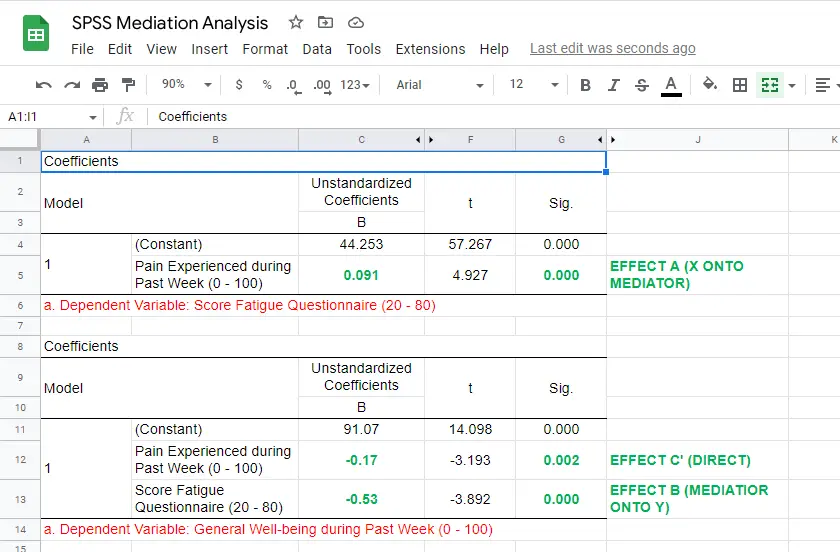
So what do we conclude? Well, all requirements for mediation are met by our results:
- effects \(a\), \(b\) and \(c\) are all statistically significant. This is because their “Sig.” or p < .05;
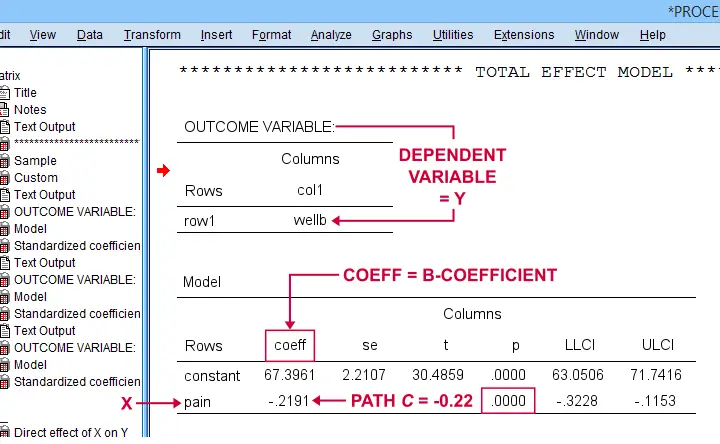
- the direct effect \(c\,'\) = -0.17 and thus closer to zero than the total effect \(c\) = -0.22.
The diagram below summarizes these results.
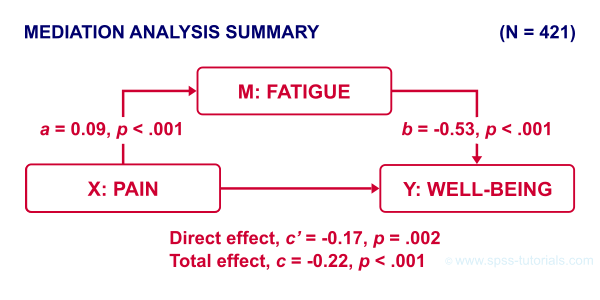
Note that both \(c\) and \(c\,'\) are significant. This is often called partial mediation: fatigue partially mediates the effect from pain onto well-being: adding it decreases the effect but doesn't nullify it altogether.
Besides partial mediation, we sometimes find full mediation. This means that \(c\) is significant but \(c\,'\) isn't: the effect is fully mediated and thus disappears when the mediator is added to the regression model.
APA Reporting Mediation Analysis
Mediation analysis is often reported as separate regression analyses as in “the first step of our analysis showed that the effect of pain on fatigue was significant, b = 0.09, p < .001...” Some authors also include t-values and degrees of freedom (df) for b-coefficients. For some very dumb reason, SPSS does not report degrees of freedom but you can compute them as
$$df = N - k - 1$$
where
- \(N\) denotes the total sample size (N = 421 in our example) and
- \(k\) denotes the number of predictors in the model (1 or 2 in our example).
Like so, we could report “the second step of our analysis showed that the effect of fatigue on well-being was also significant, b = -0.53, t(419) = -3.89, p < .001...”
Next Steps - The Sobel Test
In our analysis, the indirect effect of pain via fatigue onto well-being consists of two separate effects, \(a\) (pain onto fatigue) and \(b\) fatigue onto well-being. Now, the entire indirect effect \(ab\) is simply computed as
$$\text{indirect effect} \;ab = a \cdot b$$
This makes perfect sense: if wage \(a\) is $30 per hour and tax \(b\) is $0.20 per dollar income, then I'll pay $30 · $0.20 = $6.00 tax per hour, right?
For our example, \(ab\) = 0.09 · -0.53 = -0.049: for every unit increase in pain, well-being decreases by an average 0.049 units via fatigue. But how do we obtain the p-value and confidence interval for this indirect effect? There's 2 basic options:
- the modern literature favors bootstrapping as implemented in the PROCESS macro which we'll discuss later;
- the Sobel test (also known as “normal theory” approach).
The second approach assumes \(ab\) is normally distributed with
$$se_{ab} = \sqrt{a^2se^2_b + b^2se^2_a + se^2_a se^2_b}$$
where
\(se_{ab}\) denotes the standard error of \(ab\) and so on.
For the actual calculations, I suggest you try our Sobel Test Calculator.xlsx, partly shown below.
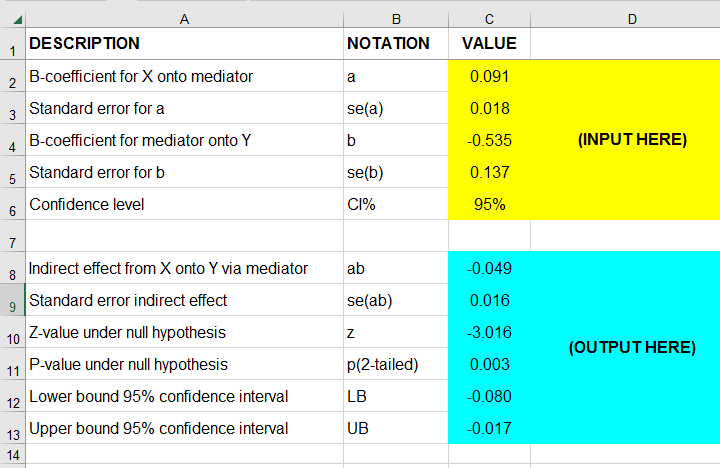
So what does this tell us? Well, our indirect effect is significant, B = -0.049, p = .002, 95% CI [-0.08, -0.02].
Next Steps - Index of Mediation
Our research variables (such as pain & fatigue) were measured on different scales without clear units of measurement. This renders it impossible to compare their effects. The solution is to report standardized coefficients known as β (Greek letter “beta”).
Our SPSS output already includes beta for most effects but not for \(ab\). However, we can easily compute it as
$$\beta_{ab} = \frac{ab \cdot SD_x}{SD_y}$$
where
\(SD_x\) is the sample-standard-deviation of our X variable and so on.
This standardized indirect effect is known as the index of mediation. For computing it, we may run something like DESCRIPTIVES pain wellb. in SPSS. After copy-pasting the resulting table into this Googlesheet, we'll compute \(\beta_{ab}\) with a quick formula as shown below.
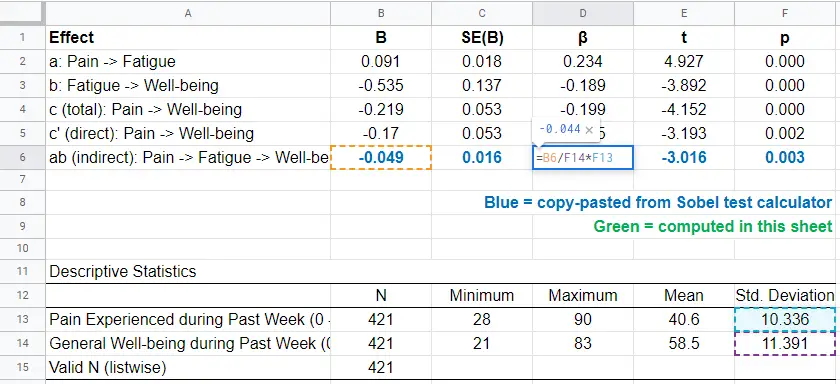
Adding the output from our Sobel test calculator to this sheet results in a very complete and clear summary table for our mediation analysis.
Final Notes
Mediation analysis in SPSS can be done with or without the PROCESS macro. Some reasons for not using PROCESS are that
- many people find PROCESS difficult to use and dislike its output format;
- PROCESS can't create regression residuals and the associated plots for checking regression assumptions such as linearity, homoscedasticity and normality;
- the PROCESS output does not include adjusted r-squared;
- PROCESS does not offer pairwise exclusion of missing values.
So why does anybody use PROCESS? Some reasons may be that
- PROCESS uses bootstrapping rather than the Sobel test. This is said to result in higher power and more accurate confidence intervals. Sadly, bootstrapping does not yield a p-value for the indirect effect whereas the Sobel test does;
- using PROCESS may save a lot of work for more complex models (parallel, serial and moderated mediation);
- if needed, PROCESS handles dummy coding for the X variable and moderators (if any);
- PROCESS doesn't require the additional calculations that we implemented in our Googlesheet: it calculates everything you need in one go.
Right. I hope this tutorial has been helpful for running, reporting and understanding mediation analysis in SPSS. This is perhaps not the easiest topic but remember that practice makes perfect.
Thanks for reading!
How to Draw Regression Lines in SPSS?
- Method A - Legacy Dialogs
- Method B - Chart Builder
- Method C - CURVEFIT
- Method D - Regression Variable Plots
- Method E - All Scatterplots Tool
Summary & Example Data
This tutorial walks you through different options for drawing (non)linear regression lines for either all cases or subgroups. All examples use bank-clean.sav, partly shown below.
Method A - Legacy Dialogs
A simple option for drawing linear regression lines is found under as illustrated by the screenshots below.
Completing these steps results in the SPSS syntax below. Running it creates a scatterplot to which we can easily add our regression line in the next step.
GRAPH
/SCATTERPLOT(BIVAR)=whours WITH salary
/MISSING=LISTWISE.
For adding a regression line, first double click the chart to open it in a Chart Editor window. Next, click the “Add Fit Line at Total” icon as shown below.
You can now simply close the fit line dialog and Chart Editor.
Result
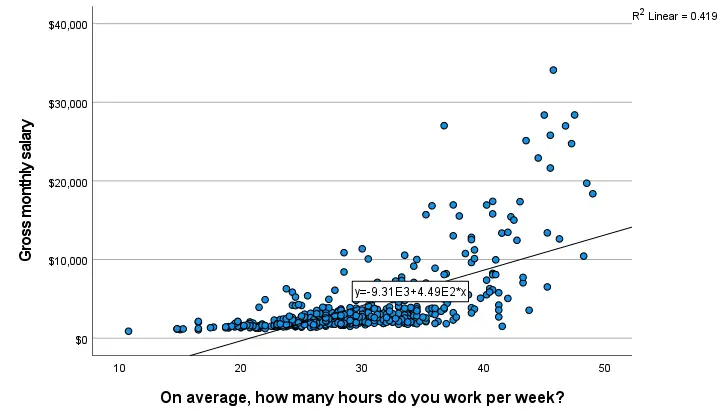
The linear regression equation is shown in the label on our line: y = 9.31E3 + 4.49E2*x which means that
$$Salary' = 9,310 + 449 \cdot Hours$$
Note that 9.31E3 is scientific notation for 9.31 · 103 = 9,310 (with some rounding).
You can verify this result and obtain more detailed output by running a simple linear regression from the syntax below.
regression
/dependent salary
/method enter whours.
When doing so, you'll also have significance levels and/or confidence intervals. Finally, note that a linear relation seems a very poor fit for these variables. So let's explore some more interesting options.
Method B - Chart Builder
For SPSS versions 25 and higher, you can obtain scatterplots with fit lines from the chart builder. Let's do so for job type groups separately: simply navigate to and fill out the dialogs as shown below.
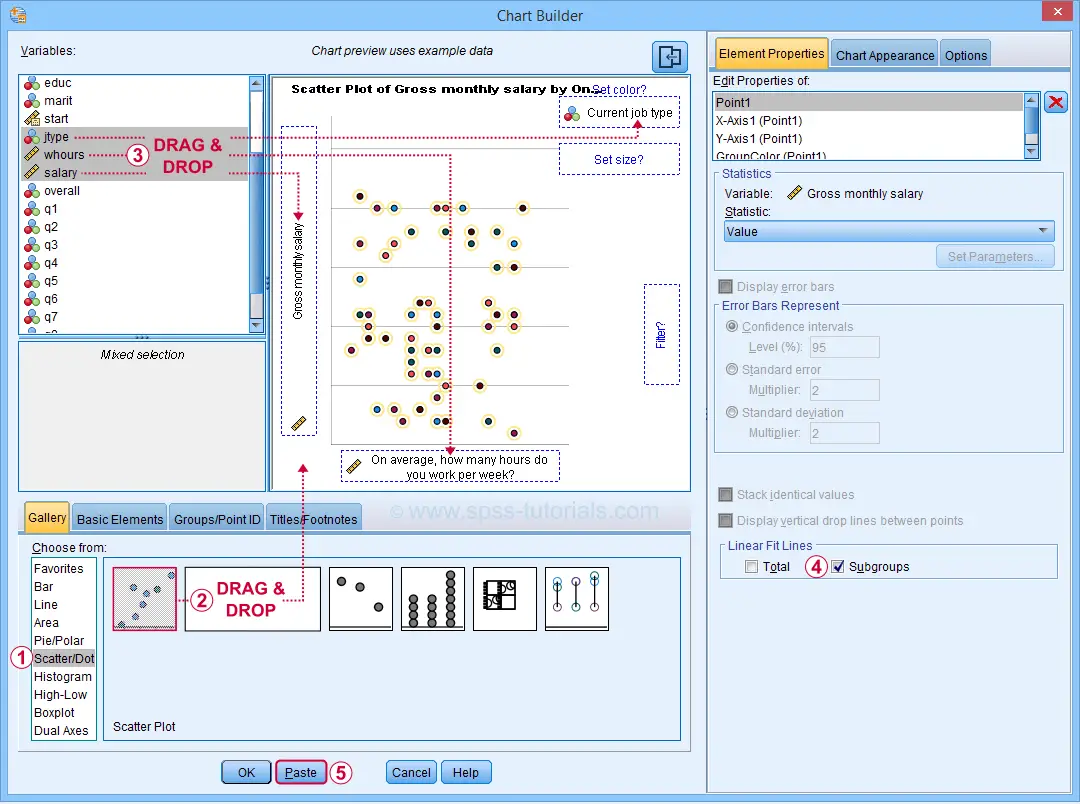
This results in the syntax below. Let's run it.
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=whours salary jtype MISSING=LISTWISE REPORTMISSING=NO
/GRAPHSPEC SOURCE=INLINE
/FITLINE TOTAL=NO SUBGROUP=YES.
BEGIN GPL
SOURCE: s=userSource(id("graphdataset"))
DATA: whours=col(source(s), name("whours"))
DATA: salary=col(source(s), name("salary"))
DATA: jtype=col(source(s), name("jtype"), unit.category())
GUIDE: axis(dim(1), label("On average, how many hours do you work per week?"))
GUIDE: axis(dim(2), label("Gross monthly salary"))
GUIDE: legend(aesthetic(aesthetic.color.interior), label("Current job type"))
GUIDE: text.title(label("Scatter Plot of Gross monthly salary by On average, how many hours do ",
"you work per week? by Current job type"))
SCALE: cat(aesthetic(aesthetic.color.interior), include(
"1", "2", "3", "4", "5"))
ELEMENT: point(position(whours*salary), color.interior(jtype))
END GPL.
Result
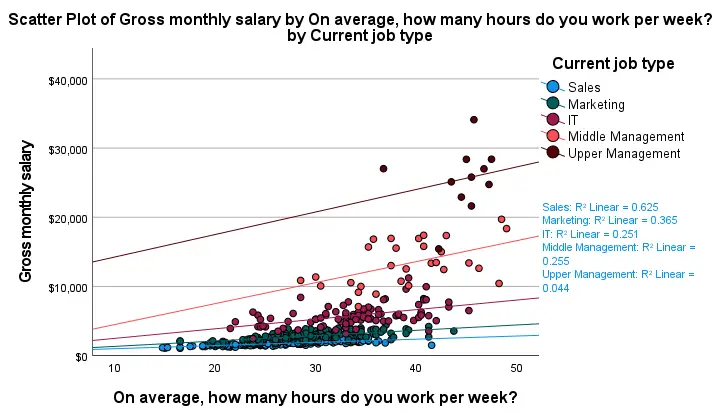
First off, this chart is mostly used for
- inspecting homogeneity of regression slopes in ANCOVA and
- simple slopes analysis in moderation regression.
Sadly, the styling for this chart is awful but we could have fixed this with a chart template if we hadn't been so damn lazy.
Anyway, note that R-square -a common effect size measure for regression- is between good and excellent for all groups except upper management. This handful of cases may be the main reason for the curvilinearity we see if we ignore the existence of subgroups.
Running the syntax below verifies the results shown in this plot and results in more detailed output.
sort cases by jtype.
split file layered by jtype.
*SIMPLE LINEAR REGRESSION.
regression
/dependent salary
/method enter whours.
*END SPLIT FILE.
split file off.
Method C - CURVEFIT
Scatterplots with (non)linear fit lines and basic regression tables are very easily obtained from CURVEFIT. Jus navigate to

 and fill out the dialog as shown below.
and fill out the dialog as shown below.
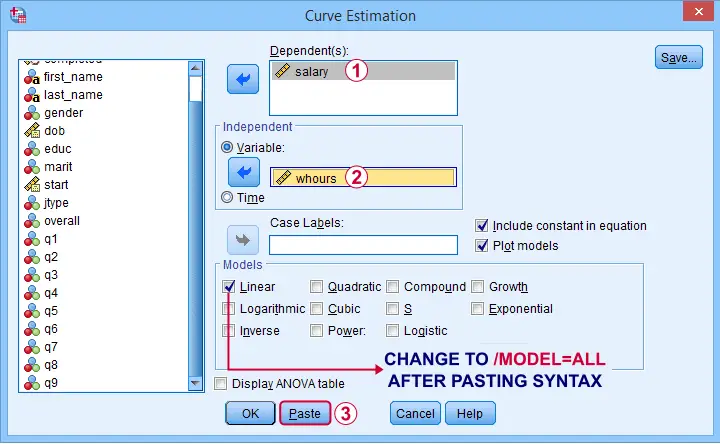
If you'd like to see all models, change /MODEL=LINEAR to /MODEL=ALL after pasting the syntax.
TSET NEWVAR=NONE.
CURVEFIT
/VARIABLES=salary WITH whours
/CONSTANT
/MODEL=ALL /* CHANGE THIS LINE MANUALLY */
/PLOT FIT.
Result
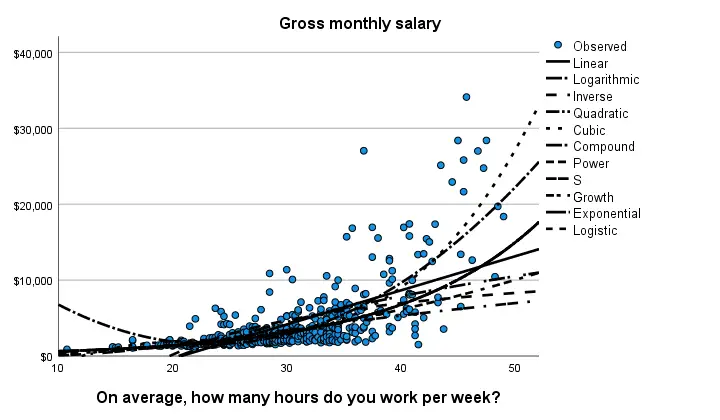
Despite the poor styling of this chart, most curves seem to fit these data better than a linear relation. This can somewhat be verified from the basic regression table shown below.
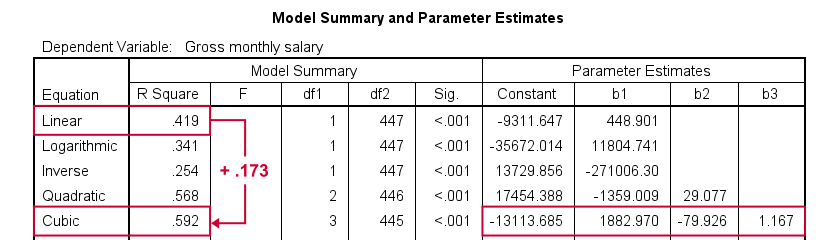
Especially the cubic model seems to fit nicely. Its equation is
$$Salary' = -13114 + 1883 \cdot hours - 80 \cdot hours^2 + 1.17 \cdot hours^3$$
Sadly, this output is rather limited: do all predictors in the cubic model seriously contribute to r-squared? The syntax below results in more detailed output and verifies our initial results.
compute whours2 = whours**2.
compute whours3 = whours**3.
regression
/dependent salary
/method forward whours whours2 whours3.
Method D - Regression Variable Plots
Regression Variable Plots is an SPSS extension that's mostly useful for
- creating several scatterplots and/or fit lines in one go;
- plotting nonlinear fit lines for separate groups;
- adding elements to and customizing these charts.
I believe this extension is preinstalled with SPSS version 26 onwards. If not, it's supposedly available from STATS_REGRESS_PLOT but I used to have some trouble installing it on older SPSS versions.
Anyway: if installed, navigating to should open the dialog shown below.
Completing these steps results in the syntax below. Let's run it.
STATS REGRESS PLOT YVARS=salary XVARS=whours COLOR=jtype
/OPTIONS CATEGORICAL=BARS GROUP=1 INDENT=15 YSCALE=75
/FITLINES CUBIC APPLYTO=GROUP.
Result
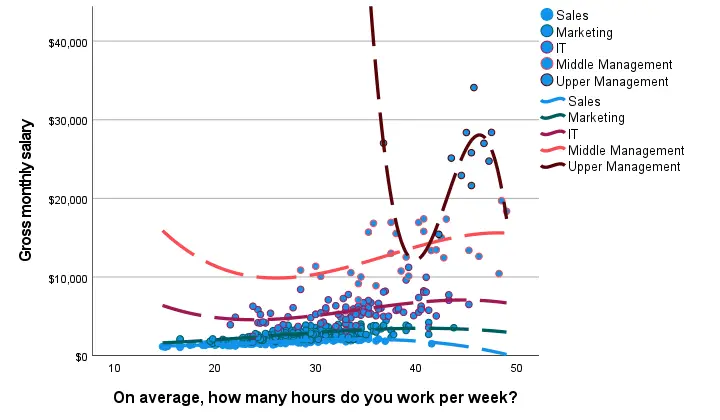
Most groups don't show strong deviations from linearity. The main exception is upper management which shows a rather bizarre curve.
However, keep in mind that these are only a handful of observations; the curve is the result of overfitting. It (probably) won't replicate in other samples and can't be taken seriously.
Method E - All Scatterplots Tool
Most methods we discussed so far are pretty good for creating a single scatterplot with a fit line. However, we often want to check several such plots for things like outliers, homoscedasticity and linearity. This is especially relevant for
A very simple tool for precisely these purposes is downloadable from and discussed in SPSS - Create All Scatterplots Tool.

Final Notes
Right, so those are the main options for obtaining scatterplots with fit lines in SPSS. I hope you enjoyed this quick tutorial as much as I have.
If you've any remarks, please throw me a comment below. And last but not least:
thanks for reading!
SPSS Mediation Analysis with PROCESS
- SPSS PROCESS Dialogs
- SPSS PROCESS Output
- Mediation Summary Diagram & Conclusion
- Indirect Effect and Index of Mediation
- APA Reporting Mediation Analysis
Introduction
A study investigated general well-being among a random sample of N = 421 hospital patients. Some of these data are in wellbeing.sav, partly shown below.

One investigator believes that
- pain increases fatigue and
- fatigue -in turn- decreases overall well-being.
That is, the relation from pain onto well-being is thought to be mediated by fatigue, as visualized below (top half).

Besides this indirect effect through fatigue, pain could also directly affect well-being (top half, path \(c\,'\)).
Now, what would happen if this model were correct and we'd (erroneously) leave fatigue out of it? Well, in this case the direct and indirect effects would be added up into a total effect (path \(c\), lower half). If all these hypotheses are correct, we should see the following in our data:
- assuming sufficient sample size, paths \(a\) and \(b\) should both be significant;
- path \(c\,'\) (direct effect) should be different from \(c\) (total effect).
One approach to such a mediation analysis is a series of (linear) regression analyses as discussed in SPSS Mediation Analysis Tutorial. An alternative, however, is using the SPSS PROCESS macro as we'll demonstrate below.
Quick Data Checks
Rather than blindly jumping into some advanced analyses, let's first see if our data look plausible in the first place. As a quick check, let's inspect the histograms of all variables involved. We'll do so from the SPSS syntax below. For more details, consult Creating Histograms in SPSS.
frequencies pain fatigue wellb
/format notable
/histogram.
Result
First off, note that all variables have N = 421 so there's no missing values. This is important to make sure because PROCESS can only handle cases that are complete on all variables involved in the analysis.
Second, there seem to be some slight outliers. This especially holds for fatigue as shown below.
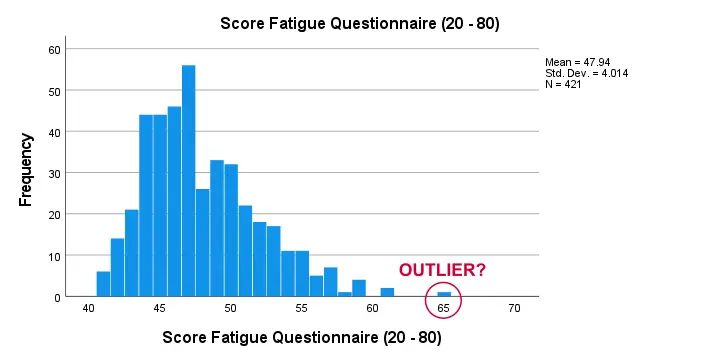
I think these values still look pretty plausible and I don't expect them to have a major impact on our analyses. Although disputable, I'll leave them in the data for now.
SPSS PROCESS Dialogs
First off, make sure you have PROCESS installed as covered in SPSS PROCESS Macro Tutorial. After opening our data in SPSS, let's navigate to as shown below.
For a simple mediation analysis, we fill out the PROCESS dialogs as shown below.
After completing these steps, you can either
- click “Ok” and just run the analysis;
- click “Paste” and run the (huge) syntax that's pasted or;
- click “Paste”, rearrange the syntax and then run it.
We discussed this last option in SPSS PROCESS Macro Tutorial. This may take you a couple of minutes but it'll pay off in the end. Our final syntax is shown below.
set mdisplay tables.
*READ PROCESS DEFINITION.
insert file = 'd:/downloaded/DEFINE-PROCESS-42.sps'.
*RUN PROCESS MODEL 4 (SIMPLE MEDIATION).
!PROCESS
y=wellb
/x=pain
/m=fatigue
/stand = 1 /* INCLUDE STANDARDIZED (BETA) COEFFICIENTS */
/total = 1 /* INCLUDE TOTAL EFFECT MODEL */
/decimals=F10.4
/boot=5000
/conf=95
/model=4
/seed = 20221227. /* MAKE BOOTSTRAPPING REPLICABLE */
SPSS PROCESS Output
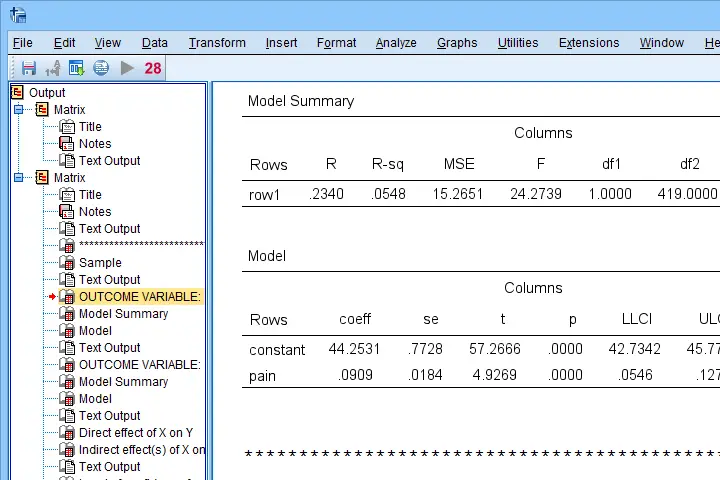
Let's first look at path \(a\): this is the effect from \(X\) (pain) onto \(M\) (fatigue). We find it in the output if we look for OUTCOME VARIABLE fatigue as shown below.
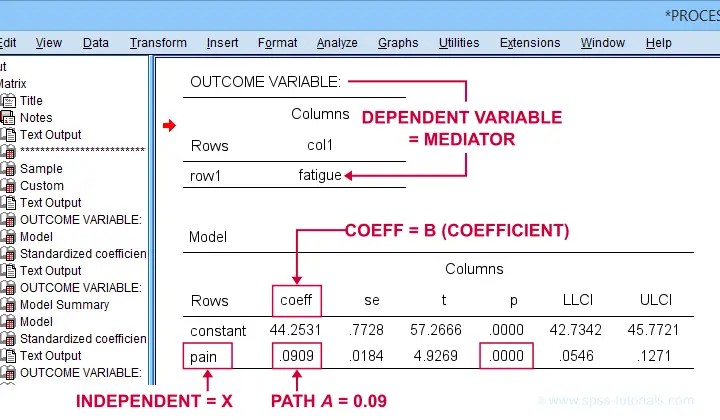
For path \(a\), b = 0.09, p < .001: on average, higher pain scores are associated with more fatigue and this is highly statistically significant. This outcome is as expected if our mediation model is correct.
SPSS PROCESS Output - Paths B and C’
Paths \(b\) and \(c\,'\) are found in a single table. It's the one for which OUTCOME VARIABLE is \(Y\) (well-being) and includes b-coefficients for both \(X\) (pain) and \(M\) fatigue.
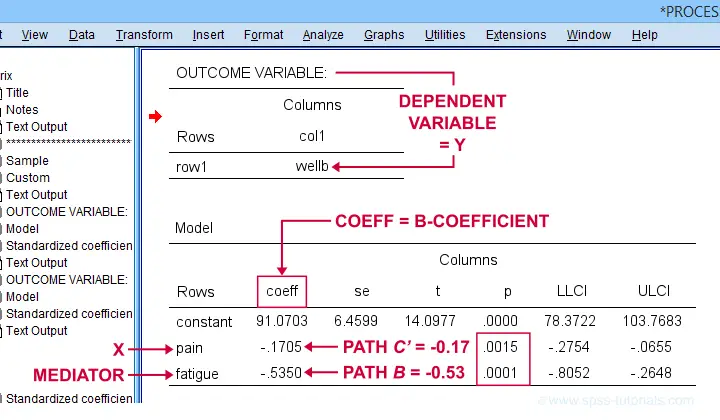
Note that path \(b\) is highly significant, as expected from our mediation hypotheses. Path \(c\,'\) (the direct effect) is also significant but our mediation model does not require this.
SPSS PROCESS Output - Path C
Some (but not all) authors also report the total effect, path \(c\). It is found in the table that has OUTCOME VARIABLE \(Y\) (well-being) that does not have a b-coefficient for the mediator.
Mediation Summary Diagram & Conclusion
The 4 main paths we examined thus far suffice for a classical mediation analysis. We summarized them in the figure below.

As hypothesized, paths \(a\) and \(b\) are both significant. Also note that direct effect is closer to zero than the total effect. This makes sense because the (negative) direct effect is the (negative) total effect minus the (negative) indirect effect.
A final point is that the direct effect is still significant: the indirect effect only partly accounts for the relation from pain onto well-being. This is known as partial mediation. A careful conclusion could thus be that
the effect from pain onto well-being
is partially mediated by fatigue.
Indirect Effect and Index of Mediation
Thus far, we established mediation by examining paths \(a\) and \(b\) separately. A more modern approach, however, focuses mostly on the entire indirect effect which is simply
$$\text{indirect effect } ab = a \cdot b$$
For our example, \(ab\) is the change in \(Y\) (well-being) associated with a 1-unit increase in \(X\) pain through \(M\) (fatigue). This indirect effect is shown in the table below.
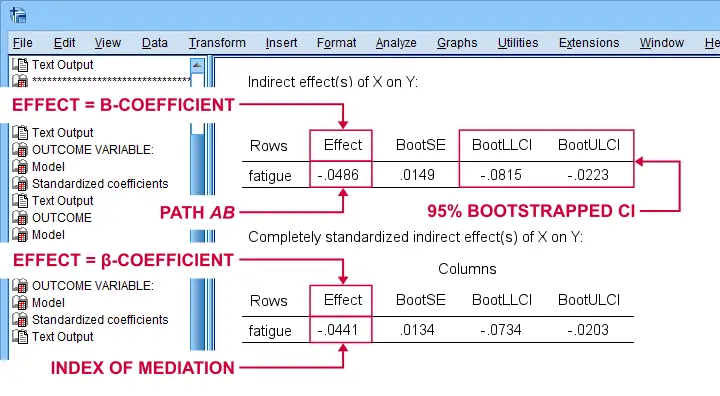
Note that PROCESS does not compute any p-value or confidence interval (CI) for \(ab\). Instead, it estimates a CI by bootstrapping. This CI may be slightly different in your output because it's based on random sampling.
Importantly, the 95% CI [-0.08, -0.02] does not contain zero. This tells us that p < .05 even though we don't have an exact p-value. An alternative for bootstrapping that does come up with a p-value here is the Sobel test.
PROCESS also reports the standardized b-coefficient for \(ab\). This is usually denoted as β and is completely unrelated to (1 - β) or power in statistics. This number, 0.04, is known as the index of mediation and is often interpreted as an effect size measure.
A huge stupidity in this table is that b is denoted as “Effect” rather than “coeff” as in the other tables. For adding to the confusion, “Effect” refers to either b or β. Denoting b as b and β as β would have been highly preferable here.
APA Reporting Mediation Analysis
Mediation analysis is often reported as separate regression analyses: “the first step of our analysis showed that the effect of pain on fatigue was significant, b = 0.09, p < .001...” Some authors also include t-values and degrees of freedom (df) for b-coefficients. For some dumb reason, PROCESS does not report degrees of freedom but you can compute them as
$$df = N - k - 1$$
where
- \(N\) denotes the total sample size (N = 421 in our example) and
- \(k\) denotes the number of predictors in the model (1 or 2 in our example).
Like so, we could report “the second step of our analysis showed that the effect of fatigue on well-being was also significant, b = -0.53, t(419) = -3.89, p < .001...”
Final Notes
First off, mediation is inherently a causal model: \(X\) causes \(M\) which, in turn, causes \(Y\). Nevertheless, mediation analysis does not usually support any causal claims. A rare exception could be \(X\) being a (possibly dichotomous) manipulation variable. In most cases, however, we can merely conclude that
our data do (not) contradict
some (causal) mediation model.
This is not quite the strong conclusion we'd usually like to draw.
A second point is that I dislike the verbose text reporting suggested by the APA. As shown below, a simple table presents our results much more clearly and concisely.
Lastly, we feel that our example analysis would have been stronger if we had standardized all variables into z-scores prior to running PROCESS. The simple reason is that unstandardized values are uninterpretable for variables such as pain, fatigue and so on. What does a pain score of 60 mean? Low? Medium? High?
In contrast: a pain z-score of -1 means one standard deviation below the mean. If these scores are normally distributed, this is roughly the 16th percentile.
This point carries over to our regression coefficients:
b-coefficients are not interpretable because
we don't know how much a “unit” is
for our (in)dependent variables. Therefore, reporting only β coefficients makes much more sense.
Now, we do have these standardized coefficients in our output. However, most confidence intervals apply to the unstandardized coefficients. This can be fixed by standardizing all variables prior to running PROCESS.
Thanks for reading!
SPSS PROCESS Macro Tutorial
- Downloading & Installing PROCESS
- Creating Tables instead of Text Output
- Using PROCESS with Syntax
- PROCESS Model Numbers
- PROCESS & Dummy Coding
- Strengths & Weaknesses of PROCESS
What is PROCESS?
PROCESS is a freely downloadable SPSS tool for estimating regression models with mediation and/or moderation effects. An example of such a model is shown below.
This model can fairly easily be estimated without PROCESS as discussed in SPSS Mediation Analysis Tutorial. However, using PROCESS has some advantages (as well as disadvantages) over a more classical approach. So how to get PROCESS and how does it work?
Those who want to follow along may download and open wellbeing.sav, partly shown below.

Note that this tutorial focuses on becoming proficient with PROCESS. The example analysis will be covered in a future tutorial.
Downloading & Installing PROCESS
PROCESS can be downloaded here (scroll down to “PROCESS macro for SPSS, SAS, and R”). The download comes as a .zip file which you first need to unzip. After doing so, in SPSS, navigate to Select “process.spd” and click “Open” as shown below.
This should work for most SPSS users on recent versions. If it doesn't, consult the installation instructions that are included with the download.
Running PROCESS
If you successfully installed PROCESS, you'll find it in the regression menu as shown below.
For a very basic mediation analysis, we fill out the dialog as shown below.
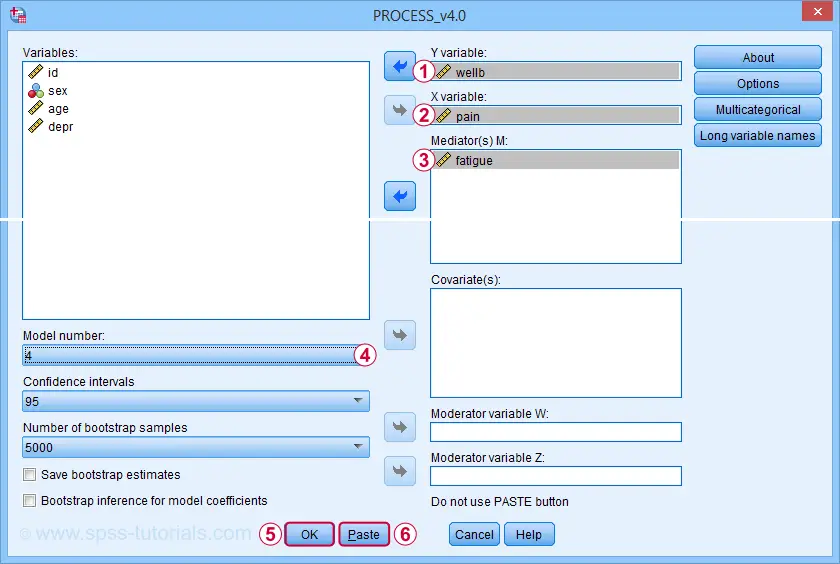
 Y refers to the dependent (or “outcome”) variable;
Y refers to the dependent (or “outcome”) variable;
 X refers to the independent variable or “predictor” in a regression context;
X refers to the independent variable or “predictor” in a regression context;
 For simple mediation, select model 4. We'll have a closer look at model numbers in a minute;
For simple mediation, select model 4. We'll have a closer look at model numbers in a minute;
 Just for now, let's click “Ok”.
Just for now, let's click “Ok”.
Result
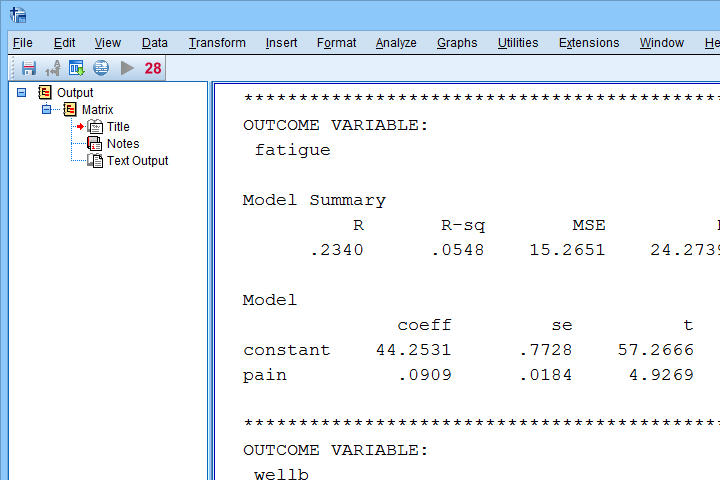
The first thing that may strike you, is that the PROCESS output comes as plain text. This is awkward because formatting it is very tedious and you can't adjust any decimal places. So let's fix that.
Creating Tables instead of Text Output
If you're using SPSS version 24 or higher, run the following SPSS syntax: set mdisplay tables. After doing so, running PROCESS will result in normal SPSS output tables rather than plain text as shown below.
Note that you can readily copy-paste these tables into Excel and/or adjust their decimal places.
Using PROCESS with Syntax
First off: whatever you do in SPSS, save your syntax. Now, like any other SPSS dialog, PROCESS has a Paste button for pasting its syntax. However, a huge stupidity from the programmers is that doing so results in some 6,140 (!) lines of syntax. I'll add the first lines below.
/* Written by Andrew F Hayes */.
/* www.afhayes.com */.
/* www.processmacro.org */.
/* Copyright 2017-2021 by Andrew F Hayes */.
/* Documented in http://www.guilford.com/p/hayes3 */.
/* THIS CODE SHOULD BE DISTRIBUTED ONLY THROUGH PROCESSMACRO.ORG */.
You can run and save this syntax but having over 6,140 lines is awkward. Now, this huge syntax basically consists of 2 parts:
- a macro definition of some 6,130 lines: this consists of the formulas and computations that are performed on the input (variables, models and so on) that the SPSS user specifies;
- a macro call of some 10 lines: this tells SPSS to run the macro and which input to use.
The macro call is at the very end of the pasted syntax (use the Ctrl + End shortcut in your syntax window) and looks as follows.
y=wellb
/x=pain
/m=fatigue
/decimals=F10.4
/boot=5000
/conf=95
/model=4.
After you run the (huge) macro definition just once during your session, you only need one (short) macro call for every PROCESS model you'd like to run.
A nice way to implement this, is to move the entire macro definition into a separate SPSS syntax file. Those who want to try this can download DEFINE-PROCESS-40.sps.
Although technically not mandatory, macro names should really start with exclamation marks. Therefore, we replaced DEFINE PROCESS with DEFINE !PROCESS in line 2,983 of this file. The final trick is that we can run this huge syntax file without opening it by using the INSERT command. Like so, the syntax below replicates our entire first PROCESS analysis.
insert file = 'd:/downloaded/DEFINE-PROCESS-40.sps'.
*RERUN FIRST PROCESS ANALYSIS.
!PROCESS
y=wellb
/x=pain
/m=fatigue
/decimals=F10.4
/boot=5000
/conf=95
/model=4.
Note: for replicating this, you may need to replace d:/downloaded by the folder where DEFINE-PROCESS-40.sps is located on your computer.
PROCESS Model Numbers
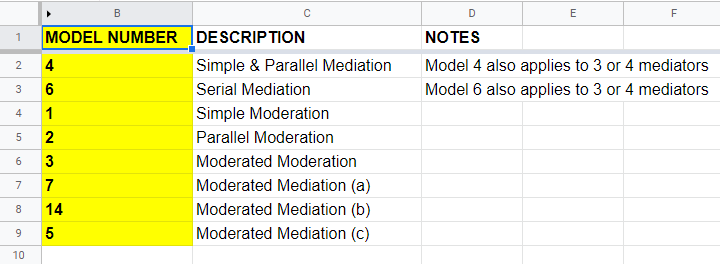
As we speak, PROCESS implements 94 models. An overview of the most common ones is shown in this Googlesheet (read-only), partly shown below.
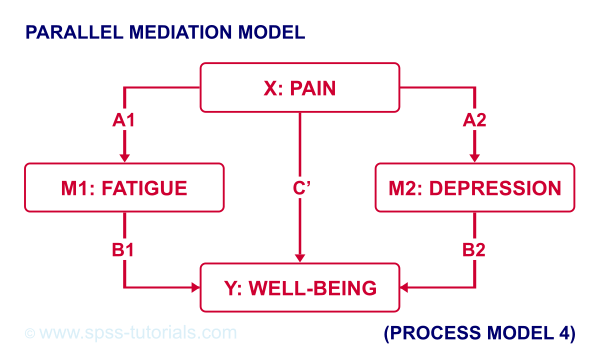
For example, if we have an X, Y and 2 mediator variables, we may hypothesize parallel mediation as illustrated below.
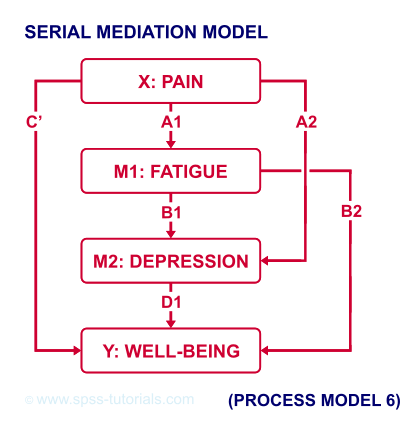
However, you could also hypothesize that mediator 1 affects mediator 2 which, in turn, affects Y. If you want to test this serial mediation effect, select model 6 in PROCESS.
For moderated mediation, things get more complicated: the moderator could act upon any combination of paths a, b or c’. If you believe the moderator only affects path c’, choose model 5 as shown below.
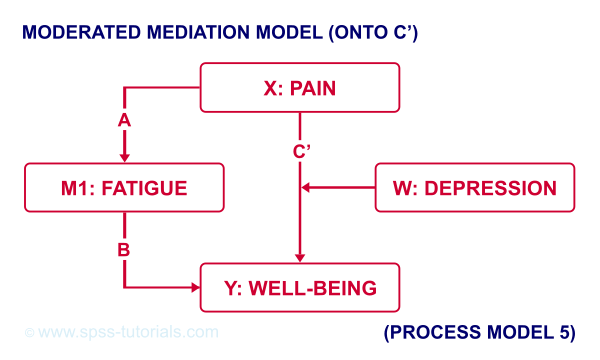
An overview of all model numbers is given in this book.
PROCESS & Dummy Coding
A quick overview of variable types for PROCESS is shown in this Googlesheet (read-only), partly shown below.
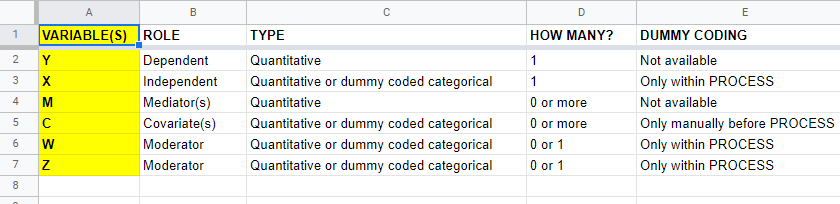
Keep in mind that PROCESS is entirely based on linear regression. This requires that dependent variables are quantitative (interval or ratio measurement level). This includes mediators, which act as both dependent and independent variables.
All other variables
- may be quantitative;
- may be dichotomous (preferably coded as 0-1);
- or must be dummy coded (nominal and ordinal variables).
X and moderator variables W and Z can only be dummy coded within PROCESS as shown below.
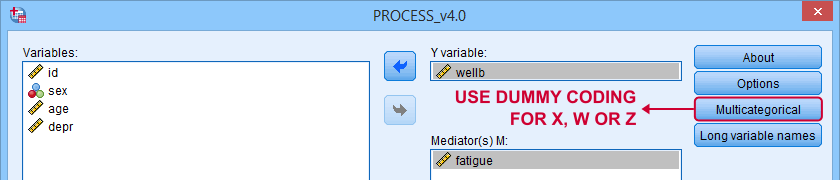
Covariates must be dummy coded before using PROCESS. For a handy tool, see SPSS Create Dummy Variables Tool.
Making Bootstrapping Replicable
Some PROCESS models rely on bootstrapping for reporting confidence intervals. Very basically, bootstrapping comes down to
- drawing a simple random sample (with replacement) from the data;
- computing statistics (for PROCESS, these are b-coefficients) on this new sample;
- repeating this procedure many (typically 1,000 - 10,000) times;
- examining to what extent each statistic fluctuates over these bootstrap samples.
Like so, a 95% bootstrapped CI for some parameter consists of the [2.5th - 97.5th] percentiles for some statistic over the bootstrap samples.
Now, due to the random nature of bootstrapping, running a PROCESS model twice typically results in slightly different CI's. This is undesirable but a fix is to add a /SEED subcommand to the macro call as shown below.
y=wellb
/x=pain
/m=fatigue
/decimals=F10.4
/boot=5000
/conf=95
/model=4
/seed = 20221227. /*MAKE BOOTSTRAPPED CI'S REPLICABLE*/
The random seed can be any positive integer. Personally, I tend to use the current date in YYYYMMDD format (20221227 is 27 December, 2022). An alternative is to run something like SET SEED 20221227. before running PROCESS. In this case, you need to prevent PROCESS from overruling this random seed, which you can do by replacing set seed = !seed. by *set seed = !seed. in line 3,022 of the macro definition.
Strengths & Weaknesses of PROCESS
A first strength of PROCESS is that it can save a lot of time and effort. This holds especially true for more complex models such as serial and moderated mediation.
Second, the bootstrapping procedure implemented in PROCESS is thought to have higher power and more accuracy than alternatives such as the Sobel test.
A weakness, though, is that PROCESS does not generate regression residuals. These are often used to examine model assumptions such as linearity and homoscedasticity as discussed in Linear Regression in SPSS - A Simple Example.
Another weakness of PROCESS is that some very basic models are not possible at all in PROCESS. A simple example is parallel moderation as illustrated below.
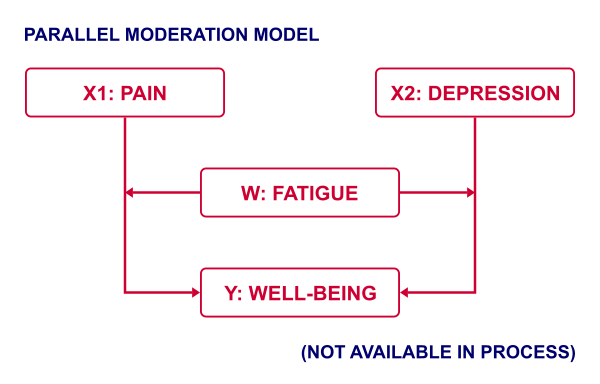
This can't be done because PROCESS is limited to a single X variable. Using just SPSS, estimating this model is a piece of cake. It's a tiny extension of the model discussed in SPSS Moderation Regression Tutorial.
A technical weakness is that PROCESS generates over 6,000 lines of syntax when pasted. The reason this happens is that PROCESS is built on 2 long deprecated SPSS techniques:
- the front end is an SPSS custom dialog (.spd) file. These have long been replaced by SPSS extension bundles (.spe files);
- the actual syntax is wrapped into a macro. SPSS macros have been deprecated in favor of Python ages ago.
I hope this will soon be fixed. There's really no need to bother SPSS users with 6,000 lines of source code.
Thanks for reading!
SPSS Moderation Regression Tutorial
- SPSS Moderation Regression - Example Data
- SPSS Moderation Regression - Dialogs
- SPSS Moderation Regression - Coefficients Output
- Simple Slopes Analysis I - Fit Lines
- Simple Slopes Analysis II - Coefficients
A sports doctor routinely measures the muscle percentages of his clients. He also asks them how many hours per week they typically spend on training. Our doctor suspects that clients who train more are also more muscled. Furthermore, he thinks that the effect of training on muscularity declines with age. In multiple regression analysis, this is known as a moderation interaction effect. The figure below illustrates it.

So how to test for such a moderation effect? Well, we usually do so in 3 steps:
- if both predictors are quantitative, we usually mean center them first;
- we then multiply the centered predictors into an interaction predictor variable;
- finally, we enter both mean centered predictors and the interaction predictor into a regression analysis.
SPSS Moderation Regression - Example Data
These 3 predictors are all present in muscle-percent-males-interaction.sav, part of which is shown below.
We did the mean centering with a simple tool which is downloadable from SPSS Mean Centering and Interaction Tool.
Alternatively, mean centering manually is not too hard either and covered in How to Mean Center Predictors in SPSS?
SPSS Moderation Regression - Dialogs
Our moderation regression is not different from any other multiple linear regression analysis: we navigate to

 and fill out the dialogs as shown below.
and fill out the dialogs as shown below.
Clicking results in the following syntax. Let's run it.
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA ZPP
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT mperc
/METHOD=ENTER cent_age cent_thours int_1
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
SPSS Moderation Regression - Coefficients Output
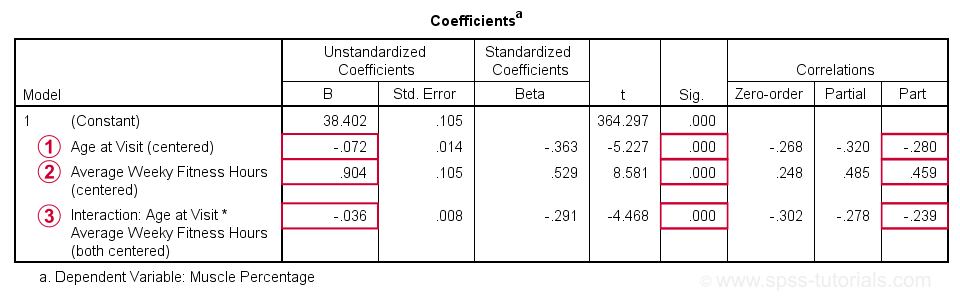
 Age is negatively related to muscle percentage. On average, clients lose 0.072 percentage points per year.
Age is negatively related to muscle percentage. On average, clients lose 0.072 percentage points per year.
 Training hours are positively related to muscle percentage: clients tend to gain 0.9 percentage points for each hour they work out per week.
Training hours are positively related to muscle percentage: clients tend to gain 0.9 percentage points for each hour they work out per week.
 The negative B-coefficient for the interaction predictor indicates that the training effect becomes more negative -or less positive- with increasing ages.
The negative B-coefficient for the interaction predictor indicates that the training effect becomes more negative -or less positive- with increasing ages.
Now, for any effect to bear any importance, it must be statistically significant and have a reasonable effect size.
At p = 0.000, all 3 effects are highly statistically significant. As effect size measures we could use the semipartial correlations (denoted as “Part”) where
- r = 0.10 indicates a small effect;
- r = 0.30 indicates a medium effect;
- r = 0.50 indicates a large effect.
The training effect is almost large and the age and age by training interaction are almost medium. Regardless of statistical significance, I think the interaction may be ignored if its part correlation r < 0.10 or so but that's clearly not the case here. We'll therefore examine the interaction in-depth by means of a simple slopes analysis.
With regard to the residual plots (not shown here), note that
- the residual histogram doesn't look entirely normally distributed but -rather- bimodal. This somewhat depends on its bin width and doesn't look too alarming;
- the residual scatterplot doesn't show any signs of heteroscedasticity or curvilinearity. Altogether, these plots don't show clear violations of the regression assumptions.
Creating Age Groups
Our simple slopes analysis starts with creating age groups. I'll go for tertile groups: the youngest, intermediate and oldest 33.3% of the clients will make up my groups. This is an arbitrary choice: we may just as well create 2, 3, 4 or whatever number of groups. Equal group sizes are not mandatory either and perhaps even somewhat unusual. In any case, the syntax below creates the age tertile groups as a new variable in our data.
rank age
/ntiles(3) into agecat3.
*Label new variable and values.
variable labels agecat3 'Age Tertile Group'.
value labels agecat3 1 'Youngest Ages' 2 'Intermediary Ages' 3 'Highest Ages'.
*Check descriptive statistics age per age group.
means age by agecat3
/cells count min max mean stddev.
Result
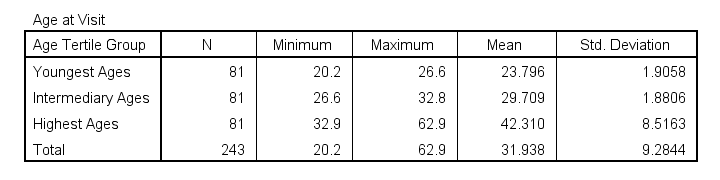
Some basic conclusions from this table are that
- our age groups have precisely equal sample sizes of n = 81;
- the group mean ages are unevenly distributed: the difference between young and intermediary -some 6 years- is much smaller than between intermediary and highest -some 13 years;
- the highest age group has a much larger standard deviation than the other 2 groups.
Points 2 and 3 are caused by the skewness in age and argue against using tertile groups. However, I think that having equal group sizes easily outweighs both disadvantages.
Simple Slopes Analysis I - Fit Lines
Let's now visualize the moderation interaction between age and training. We'll start off creating a scatterplot as shown below.
Clicking results in the syntax below.
GRAPH
/SCATTERPLOT(BIVAR)=thours WITH mperc BY agecat3
/MISSING=LISTWISE
/TITLE='Muscle Percentage by Training Hours by Age Group'.
*After running chart, add separate fit lines manually.
Adding Separate Fit Lines to Scatterplot
After creating our scatterplot, we'll edit it by double-clicking it. In the Chart Editor window that opens, we click the icon labeled Add Fit Line at Subgroups
After adding the fit lines, we'll simply close the chart editor. Minor note: scatterplots with (separate) fit lines can be created in one go from the Chart Builder in SPSS version 25+ but we'll cover that some other time.
Result
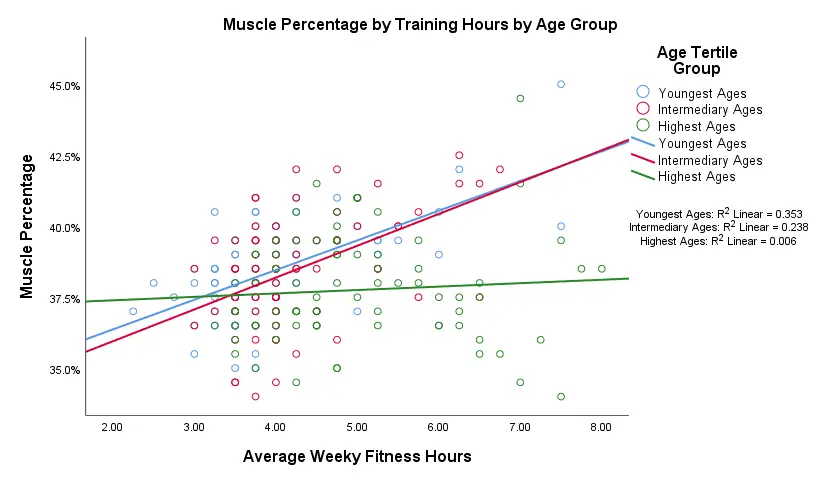
Our fit lines nicely explain the nature of our age by training interaction effect:
- the 2 youngest age groups show a steady increase in muscle percentage by training hours;
- for the oldest clients, however, training seems to hardly affect muscle percentage. This is how the effect of training on muscle percentage is moderated by age;
- on average, the 3 lines increase. This is the main effect of training;
- overall, the fit line for the oldest group is lower than for the other 2 groups. This is our main effect of age.
Again, the similarity between the 2 youngest groups may be due to the skewness in ages: the mean ages for these groups aren't too different but very different from the highest age group.
Simple Slopes Analysis II - Coefficients
After visualizing our interaction effect, let's now test it: we'll run a simple linear regression of training on muscle percentage for our 3 age groups separately. A nice way for doing so in SPSS is by using SPLIT FILE.
The REGRESSION syntax was created from the menu as previously but with (uncentered) training as the only predictor.
sort cases by agecat3.
split file layered by agecat3.
*Run simple linear regression with uncentered training hours on muscle percentage.
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA ZPP
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT mperc
/METHOD=ENTER thours
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID).
*Split file off.
split file off.
Result
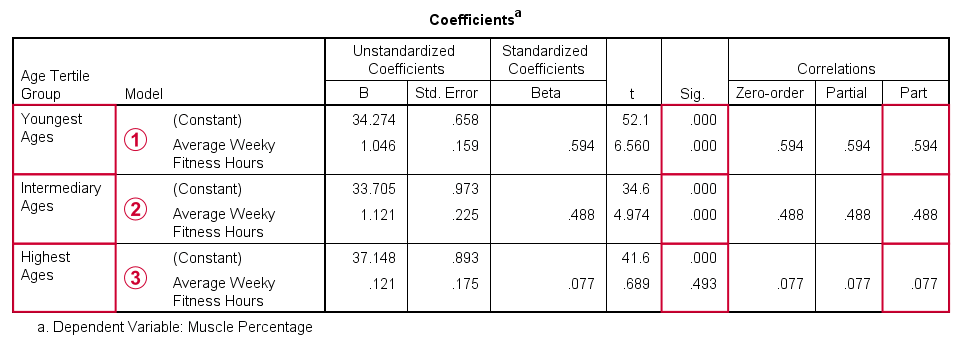
The coefficients table confirms our previous results:
 for the youngest age group, the training effect is statistically significant at p = 0.000. Moreover, its part correlation of r = 0.59 indicates a large effect;
for the youngest age group, the training effect is statistically significant at p = 0.000. Moreover, its part correlation of r = 0.59 indicates a large effect;
 the results for the intermediary age group are roughly similar to the youngest group;
the results for the intermediary age group are roughly similar to the youngest group;
 for the highest age group, the part correlation of r = 0.077 is not substantial. We wouldn't take it seriously even if it had been statistically significant -which it isn't at p = 0.49.
for the highest age group, the part correlation of r = 0.077 is not substantial. We wouldn't take it seriously even if it had been statistically significant -which it isn't at p = 0.49.
Last, the residual histograms (not shown here) don't show anything unusual. The residual scatterplot for the oldest age group looks curvilinear except from some outliers. We should perhaps take a closer look at this analysis but we'll leave that for another day.
Thanks for reading!
SPSS – Create Dummy Variables Tool
Categorical variables can't readily be used as predictors in multiple regression analysis. They must be split up into dichotomous variables known as “dummy variables”. This tutorial offers a simple tool for creating them.
- Example Data File
- Prerequisites and Installation
- Example I - Numeric Categorical Variable
- Example II - Categorical String Variable
Example Data File
We'll demonstrate our tool on 2 examples: a numeric and a string variable. Both variables are in staff.sav, partly shown below.
We encourage you to download and open this data file in SPSS and replicate the examples we'll present.
Prerequisites and Installation
Our tool requires SPSS version 24 or higher. Also, the SPSS Python 3 essentials must be installed (usually the case with recent SPSS versions).
Next, click SPSS_TUTORIALS_DUMMIFY.spe in order to download our tool. For installing it, navigate to
 as shown below.
as shown below.

In the dialog that opens, navigate to the downloaded .spe file and install it. SPSS will then confirm that the extension was successfully installed under

Example I - Numeric Categorical Variable
Let's now dummify Marital Status. Before doing so, we recommend you first inspect its basic frequency distribution as shown below.
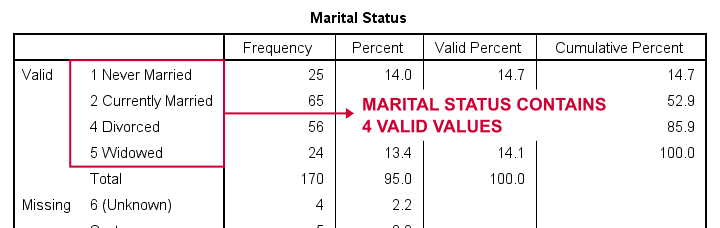
Importantly, note that Marital Status contains 4 valid (non missing) values. As we'll explain later on, we always need to exclude one category, known as the reference category. We'll therefore create 3 dummy variables to represent our 4 categories.
We'll do so by navigating to
 as shown below.
as shown below.

Let's now fill out the dialog that pops up.
 We choose the first category (“Never Married”) as our reference category. Completing these results in the syntax below. Let's run it.
We choose the first category (“Never Married”) as our reference category. Completing these results in the syntax below. Let's run it.
SPSS TUTORIALS DUMMIFY VARIABLES=marit
/OPTIONS NEWLABELS=LABLAB REFCAT=FIRST ACTION=RUN.
Result
Our tool has now created 3 dummy variables in the active dataset. Let's compare them to the value labels of our original variable, Marital Status.
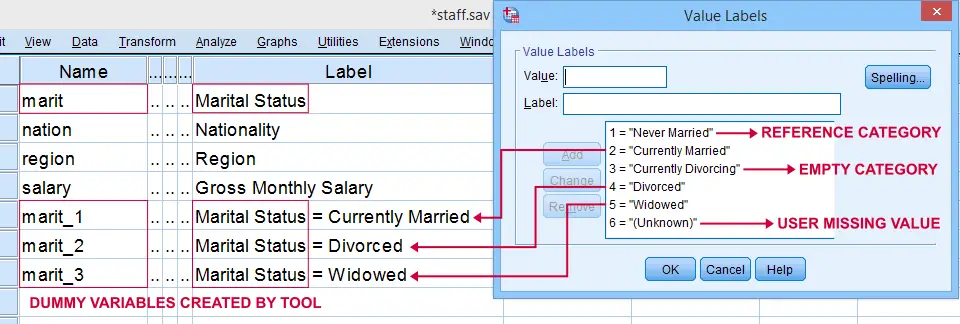
First note that the variable names for our dummy variables are the original variable name plus an integer suffix. These suffixes don't usually correspond to the categories they represent.
Instead, these categories are found in the variable labels for our dummy variables. In this example, they are based on the variable and value labels in Marital Status.
Next, note that some categories were skipped for the following reasons:
- no dummy variable was created for “Never Married” because we chose it as our reference category;
- no dummy variable was created for “Currently Divorcing” because it doesn't actually occur in our dataset;
- no dummy variable was created for “(Unknown)” because it is a user missing value.
Now the big question is:
are these results correct?
An easy way to confirm that they are indeed correct is actually running a dummy variable regression. We'll then run the exact same analysis with a basic ANOVA.
For example, let's try and predict Salary from Marital Status via both methods by running the syntax below.
regression
/dependent salary
/method enter marit_1 to marit_3.
*Compare mean salaries by marital status via ANOVA.
means salary by marit
/statistics anova.
First note that the regression r-square of 0.089 is identical to the eta squared of 0.089 in our ANOVA results. This makes sense because they both indicate the proportion of variance in Salary accounted for by Marital Status.
Also, our ANOVA comes up with a significance level of p = 0.002 just as our regression analysis does. We could even replicate the regression B-coefficients and their confidence intervals via ANOVA (we'll do so in a later tutorial). But for now, let's just conclude that the results are correct.
Example II - Categorical String Variable
Let's now dummify Job Type, a string variable. Again, we'll start off by inspecting its frequencies and we'll probably want to specify some missing values. As discussed in SPSS - Missing Values for String Variables, doing so is cumbersome but the syntax below does the job.
frequencies jtype.
*Change '(Unknown)' into 'NA'.
recode jtype ( '(Unknown)' = 'NA').
*Set empty string value and 'NA' as user missing values.
missing values jtype ('','NA').
*Reinspect basic frequency table.
frequencies jtype.
Result
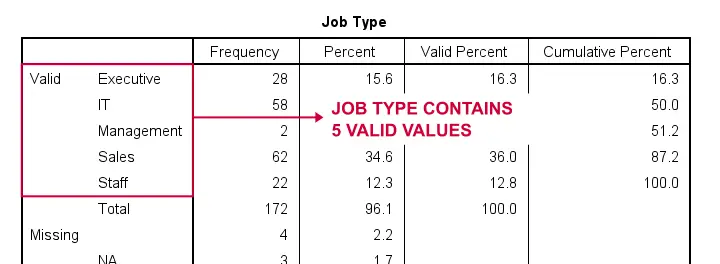
Again, we'll first navigate to
 and we'll fill in the dialog as shown below.
and we'll fill in the dialog as shown below.
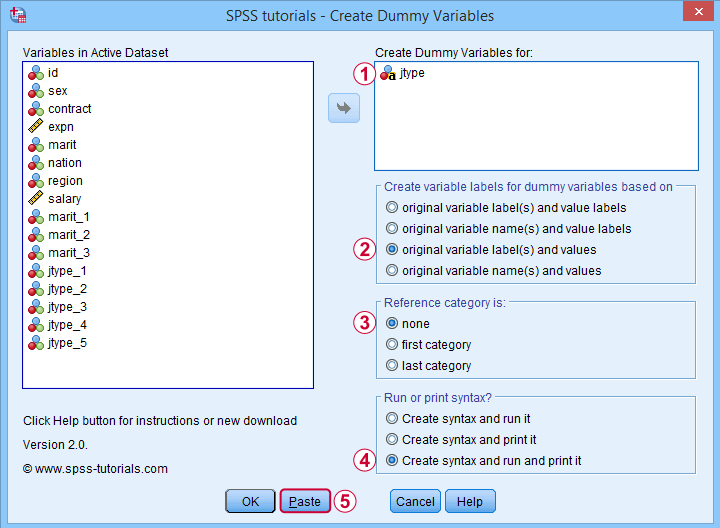
 For string variables, the values themselves usually describe their categories. We therefore throw values (instead of value labels) into the variable labels for our dummy variables.
For string variables, the values themselves usually describe their categories. We therefore throw values (instead of value labels) into the variable labels for our dummy variables.
 If we neither want the first nor the last category as reference, we'll select “none”. In this case, we must manually exclude one of these dummy variables from the regression analysis that follows.
If we neither want the first nor the last category as reference, we'll select “none”. In this case, we must manually exclude one of these dummy variables from the regression analysis that follows.
 Besides creating dummy variables, we may also want to inspect the syntax that's created and run by the tool. We may also copy, paste, edit and run it from a syntax window instead of having our tool do that for us.
Besides creating dummy variables, we may also want to inspect the syntax that's created and run by the tool. We may also copy, paste, edit and run it from a syntax window instead of having our tool do that for us.
Completing these steps result in the syntax below.
SPSS TUTORIALS DUMMIFY VARIABLES=jtype
/OPTIONS NEWLABELS=LABVAL REFCAT=NONE ACTION=BOTH.
Result
Besides creating 5 dummy variables, our tool also prints the syntax that was used in the output window as shown below.

Finally, if you didn't choose any reference category, you must exclude one of the dummy variables from your regression analysis. The syntax below shows what happens if you don't.
regression
/dependent salary
/method enter jtype_1 jtype_2 jtype_3 jtype_4 jtype_5.
*Compare salaries by Job Type right way: reference category = 4 (sales).
regression
/dependent salary
/method enter jtype_1 jtype_2 jtype_3 jtype_5.
The first example is a textbook illustration of perfect multicollinearity: the score on some predictor can be perfectly predicted from some other predictor(s). This makes sense: a respondent scoring 0 on the first 4 dummies must score 1 on the last (and reversely).
In this situation, B-coefficients can't be estimated. Therefore, SPSS excludes a predictor from the analysis as shown below.

Note that tolerance is the proportion of variance in a predictor that can not be accounted for by other predictors in the model. A tolerance of 0.000 thus means that some predictor can be 100% -or perfectly- predicted from the other predictors.
Thanks for reading!
How to Create Dummy Variables in SPSS?
You can't readily use categorical variables as predictors in linear regression: you need to break them up into dichotomous variables known as dummy variables.
The ideal way to create these is our dummy variables tool. If you don't want to use this tool, then this tutorial shows the right way to do it manually.
- Example I - Any Numeric Variable
- Example II - Numeric Variable with Adjacent Integers
- Example III - String Variable with Conversion
- Example IV - String Variable without Conversion
Example Data File
This tutorial uses staff.sav throughout. Part of this data file is shown below.
Example I - Any Numeric Variable
Let's first create dummy variables for marit, short for marital status. Our first step is to run a basic FREQUENCIES table with frequencies marit. The table below shows the resulting table.
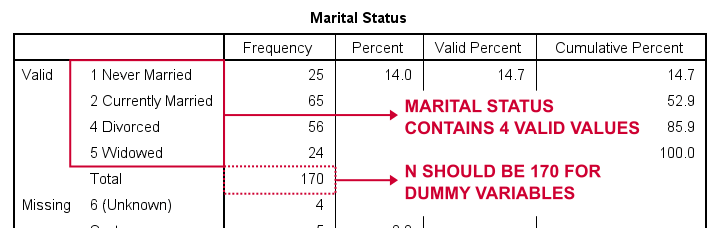
So how to break up marital status into dummy variables? First off, we always omit one category, the reference category. You may choose any category as the reference category.
So for this example, we choose 5 (Widowed). This implies that we'll create 3 dummy variables representing categories 1, 2 and 4 (note that 3 does not occur in this variable).
The syntax below shows how to create and label our 3 dummy variables. Let's run it.
compute marit_1 = (marit = 1).
compute marit_2 = (marit = 2).
compute marit_4 = (marit = 4).
*Apply variable labels to dummy variables.
variable labels
marit_1 'Marital Status = Never Married'
marit_2 'Marital Status = Currently Married'
marit_4 'Marital Status = Divorced'.
*Quick check first dummy variable
frequencies marit_1.
Results
First off, note that we created 3 nicely labelled dummy variables in our active dataset.
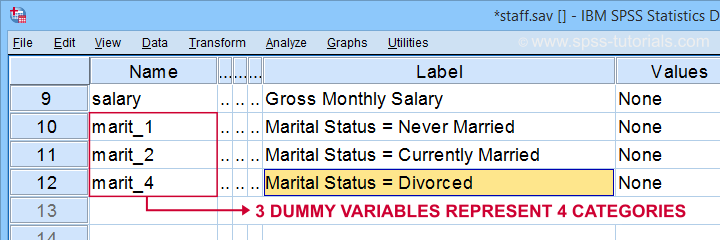
The table below shows the frequency distribution for our first dummy variable.

Note that our dummy variable holds 3 distinct values:
- respondents whose marital status is not “never married” score 0;
- respondents whose marital status is “never married” score 1;
- respondents whose marital status is a missing value (and therefore unknown) have a system missing value.
We may now check the results more thoroughly by running crosstabs marit by marit_1 to marit_4. Doing so creates 3 contingency tables, the first of which is shown below.
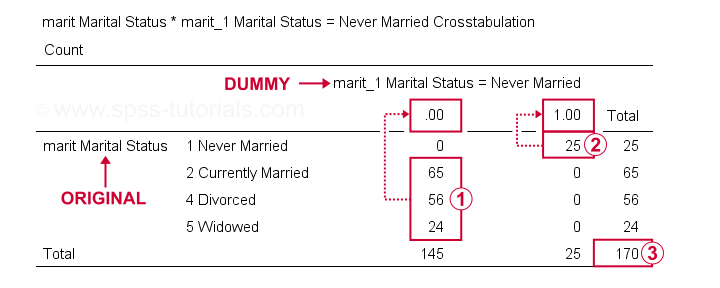
On our dummy variable,
 respondents having other marital statuses than “never married” all score 0;
respondents having other marital statuses than “never married” all score 0;
 respondents who “never married” all score 1;
respondents who “never married” all score 1;
 we've a sample size of N = 170 (this table only includes respondents without missing values on either variable).
we've a sample size of N = 170 (this table only includes respondents without missing values on either variable).
Optionally, a final -very thorough- check is to compare ANOVA results for the original variable to regression results using our dummy variables. The syntax below does just that, using monthly salary as the dependent variable.
regression
/dependent salary
/method enter marit_1 to marit_4.
*Minimal ANOVA using original variable.
oneway salary by marit.
Note that both analyses result in identical ANOVA tables. We'll discuss ANOVA versus dummy variable regression more thoroughly in a future tutorial.
Example II - Numeric Variable with Adjacent Integers
We'll now create dummy variables for region. Again, we start off by inspecting a minimal frequency table which we'll create by running frequencies region. This results in the table below.
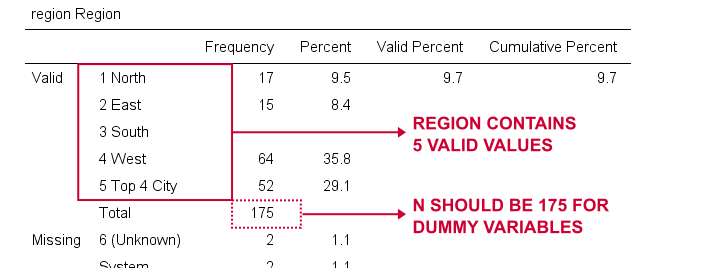
We'll choose 1 (“North”) as our reference category. We'll therefore create dummy variables for categories 2 through 5. Since these are adjacent integers, we can speed things up by using DO REPEAT as shown below.
do repeat #vals = 2 to 5 / #vars = region_2 to region_5.
recode region (#vals = 1)(lo thru hi = 0) into #vars.
end repeat print.
*Apply variable labels to new variables.
variable labels
region_2 'Region = East'
region_3 'Region = South'
region_4 'Region = West'
region_5 'Region = Top 4 City'.
*Quick check.
crosstabs region by region_2 to region_5.
A careful inspection of the resulting tables confirms that all results are correct.
Example III - String Variable with Conversion
Sadly, our first 2 methods don't work for string variables such as jtype -short for “job type”). The easiest solution is to convert it into a numeric variable as discussed in SPSS Convert String to Numeric Variable. The syntax below uses AUTORECODE to get the job done.
autorecode jtype
/into njtype.
*Check result.
frequencies njtype.
*Set missing values.
missing values njtype (1,2).
*Recheck result.
frequencies njtype.
Result

Since njtype -short for “numeric job type”- is a numeric variable, we can now use method I or method II for breaking it up into dummy variables.
Example IV - String Variable without Conversion
Converting string variables into numeric ones is the easy to create dummy variables for them. Without this conversion, the process is cumbersome because SPSS doesn't handle missing values for string variables properly. However, syntax below gets the job done correctly.
frequencies jtype.
*Chance '(Unknown)' into 'NA'.
recode jtype ('(Unknown)' = 'NA').
*Set user missing values.
missing values jtype ('','NA').
*Reinspect frequencies.
frequencies jtype.
*Create dummy variables for string variable.
if(not missing(jtype)) jtype_1 = (jtype = 'IT').
if(not missing(jtype)) jtype_2 = (jtype = 'Management').
if(not missing(jtype)) jtype_3 = (jtype = 'Sales').
if(not missing(jtype)) jtype_4 = (jtype = 'Staff').
*Apply variable labels to dummy variables.
variable labels
jtype_1 'Job type = IT'
jtype_2 'Job type = Management'
jtype_3 'Job type = Sales'
jtype_4 'Job type = Staff'.
*Check results.
crosstabs jtype by jtype_1 to jtype_4.
Final Notes
Creating dummy variables for numeric variables can be done fast and easily. Setting proper variable labels, however, always takes a bit of work. String variables require some extra step(s) but are pretty doable as well.
Nevertheless, the easiest option is our SPSS Create Dummy Variables Tool as it takes perfect care of everything.
Hope you found this tutorial helpful! Let us know by throwing a comment below.
Thanks for reading!
 SPSS TUTORIALS
SPSS TUTORIALS